Лабораторная работа № 2. 2. ТЕОРИЯ. 3. ОБОРУДОВАНИЕ. 4. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

Лабораторная работа № 2

Измерение ускорения свободного падения с помощью математического маятника/

1. ЦЕЛЬ РАБОТЫ:

-приобрести навыки исследовательской работы;

-научиться измерять ускорение свободного падения с помощью математического маятника.

2. ТЕОРИЯ

Математическим маятником называется материальная точка, подвешенная на невесомой и нерастяжимой нити. Моделью такого маятника может служить шарик, подвешенный на длинной нити.

На основании многочисленных опытов установлены законы колебания математического маятника:

- период колебаний не зависит от массы маятника и амплитуды его колебаний, если угол размаха не превышает 6;

- период колебаний математического маятника прямо пропорционален корню квадратному из длины нити и обратно пропорционален корню квадратному из ускорения свободного падения: ;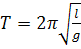

Из этой формулы можно найти ускорение свободного падения: .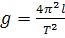

3. ОБОРУДОВАНИЕ

- штатив с держателем;

- шарик с нитью длиной не менее 1 м.;

- пробка с прорезью в боковой поверхности;

- метровая линейка;

- штангенциркуль;

- секундомер.

4. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

4. 1. Поместить штатив с держателем на край стола.

4. 2. Укрепить свободный конец нити шарика в прорези пробки и зажать пробку в держателе.

4. 3. Измерить диаметр шарика штангенциркулем, длину нити линейкой.

4. 4. Отклонить шарик на небольшой угол и отпустить. По секундомеру определить время t, за которое маятник совершит n полных колебаний, например 50.

4. 5. Вычислить период полного колебания маятника: .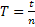

4. 6. Используя формулу периода колебаний математического маятника, вычислить ускорение свободного падения.

4. 7. Опят повторить 2-3 раза, меняя длину маятника и число его полных колебаний.

4. 8. Определить среднее значение g_ср и найти относительную погрешность.

4. 9. Результат измерений и вычислений записать в таблицу.

4. 10. Сравнить результат опыта с табличным значением ускорения свободного падения для данной географической широты.

12 Следующая ⇒