
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Алгебра 8 класс. Тема урока: «Квадратный трехчлен»
Алгебра 8 класс
Тема урока: «Квадратный трехчлен»
Тип урока: урок расширения знаний
Цель урока: узнать, что такое квадратный трехчлен, разложение квадратного трехчлена на множители
Список ресурсов:
1. Учебник «Алгебра 8», Мерзляк Н. Я. и др. 2018 «Вентана-Граф»,
§22, стр. 180-182
Все возникающие вопросы по урочной и домашней работе можно задать учителю в личных сообщениях 89065894300
Замечание: при разложении квадратного трехчлена на множители используются знания: вынесение общего множителя за скобки, формула нахождения дискриминанта квадратного уравнения, формула нахождения корней квадратного уравнения, теорема Виета.
Порядок действий учащего во время урока:
| №п/п | Вид деятельности | Рекомендации по выполнению | Время выполнения |
| Читаем и изучаем теоретический материал «Квадратный трехчлен» §22, стр. стр. 180-182 | 3 минуты | ||
Записываем краткий конспект:
Многочлен ах2 + вх +с -квадратный трёхчлен, где х – переменная, а, в, с –некоторые числа, а ≠ 0.
Рассмотреть примеры квадратных трехчленов (не записывать)
не записывать Корень квадратного трехчлена – значение переменной, при котором значение квадратного трехчлена равно нулю.
D = b2 – 4ac – дискриминант квадратного трехчлена.
не записывать Если D < 0, то нет корней, если D = 0, то один корень, если D > 0, то два корня.
Квадратный трехчлен можно разложить на линейные множители:
1) методом группировки
х2 – 3х + 2 = х2 – х – 2х + 2 = х(х – 1) – 2(х – 1) =
= (х – 2)(х – 1)
2) методом нахождения дискриминанта и корней квадратного уравнения
Теорема 22. 1. Если D > 0, то трехчлен можно разложить на множители.
ах2 + вх +с = а(х – х1)(х – х2), где х1, х2 – корни.
Если D = 0, то х1=х2 и ах2 + вх +с = а(х – х1)2.
Теорема 22. 2. Если D < 0, то трехчлен нельзя разложить на множители.
Пример1 Разложить на множители квадратный трехчлен:
1) – х2 + 17х – 30
Найдем корни квадратного трехчлена:
– х2 + 17х – 30 = 0
а = - 1, b = 17, с = - 30
D = b2 – 4ac; D = 172 – 4( - 1) ( - 30) = 289 – 120 = 169.
D > 0, значит уравнение имеет 2 корня.
х12 = 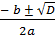 ; х12 = ; х12 =  = = 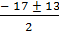 х1 = 2, х2 = 15
Следовательно – х2 + 17х – 30 = - (х – 2)(х – 15).
2) 3х2 - 7х + 30
Найдем корни квадратного трехчлена:
3х2 - 7х + 2
а = 3, b = -7, с = 2
D = b2 – 4ac; D = (-7)2 – 4∙ 3∙ 2 = 49 – 24 = 25.
D > 0, значит уравнение имеет 2 корня.
х12 =
х1 = 2, х2 = 15
Следовательно – х2 + 17х – 30 = - (х – 2)(х – 15).
2) 3х2 - 7х + 30
Найдем корни квадратного трехчлена:
3х2 - 7х + 2
а = 3, b = -7, с = 2
D = b2 – 4ac; D = (-7)2 – 4∙ 3∙ 2 = 49 – 24 = 25.
D > 0, значит уравнение имеет 2 корня.
х12 = 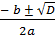 ; х12 = ; х12 =  = = 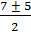 х1 =
х1 =  , х2 = 2
Следовательно 3х2 - 7х + 2= 3(х – , х2 = 2
Следовательно 3х2 - 7х + 2= 3(х –  )(х – 2) =
= (3х – 1)(х – 2).
Пример 2. Списать на стр. 182
Пример 3. Списать на стр. 182 )(х – 2) =
= (3х – 1)(х – 2).
Пример 2. Списать на стр. 182
Пример 3. Списать на стр. 182
| При выполнении задания пользоваться учебником или звонить учителю, если трудно и непонятно Корни можно найти по теореме Виета | 10 мин | |
| Выполняем письменно задания в тетради из учебника на стр. 183 №753(3, 6), 755(1, 3) использовать вынесение общего множителя за скобки в №755(3) в числителе. | Выполнять по аналогии с рассмотренными примерами или звонить учителю. | 17 минут | |
| Записываем домашнее задание: §22, стр. 180-182, вопр., №754(1, 4), 756(3) использовать вынесение общего множителя за скобки в №756(3) в знаменателе. | После выполнения классного и домашнего задания, скан САМОСТОЯТЕЛЬНО РЕШЕННЫХ заданий загрузить на мой вацап | ||
| 3 минуты – время для самоорганизации! |
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|