14 февраля 2022 г. (понедельник)

14 февраля 2022 г. (понедельник)

Дисциплина: Математика

Группа: № 83

Урок № 75

Тема: Двугранный угол.

Цель:

Учебная: рассмотреть понятие двугранного угла.

Развивающая: развивать математическое мышление, графические и вычислительные навыки, пространственное воображение.

Воспитательная: воспитывать у обучающихся устойчивый интерес к изучению математики; математическую культуру.

Литература: Геометрия. 10-11 классы: учеб. для общеобразоват. организаций: базовый и углубл. уровни / Л. С. Атанасян, В. Ф. Бутузов [и др. ] – М.: Просвещение, 2013.

Материалы урока: !!! РИСУЕМ ПРАВИЛЬНО, НЕ МЕНЕЕ 5 СМ!

b a а

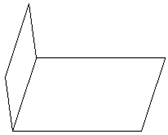
Две пересекающиеся плоскости разбивают пространство на четыре части, каждая из которых носит название двугранного угла, образованного этими плоскостями. Двугранным углом называется фигура, образованная двумя полуплоскостями (a и b) с общей ограничивающей их прямой (a). Полуплоскости называются гранями, ограничивающая их прямая – ребром двугранного угла.

Мера двугранного угла – линейный угол двугранного угла.

Введём понятие линейного угла двугранного угла.

М В g А а b a

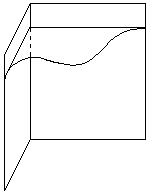
На ребре а возьмём произвольную точку М и проведём через неё в каждой полуплоскости прямые АМ и ВМ, перпендикулярные к ребру а. Эти прямые образуют плоский угол, принимаемый за меру двугранного угла. Т. к. обе прямые перпендикулярны к ребру угла, то и плоскость g, в которой они лежат, g ^ а. Поэтому плоский Ð АМВ можно получить, рассекая двугранный угол плоскостью g.

Задача.

Из точек А и В, лежащих в гранях двугранного угла, опущены перпендикуляры АА₁ и ВВ₁ на ребро угла. Найдите длину отрезка АВ, если АА₁ = а, ВВ₁ = в, А₁В₁ = с и двугранный угол равен a.

Решение.

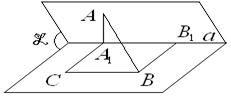Пусть дан двугранный угол с ребром а, АА₁ ^ а, ВВ₁ ^ а, АА₁ = а, ВВ₁ = в, А₁В₁ = с. Найдём АВ.

А₁С || ВВ₁, Ð АА₁С = a.

Четырёхугольник СА₁В₁В – параллелограмм.

Из D АА₁С по теореме косинусов:

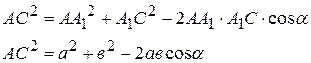
Из D АВС – прямоугольного (Ð С = 90^о) по теореме Пифагора: АВ² = АС² + ВС²;

АВ² = а² + в² – 2авсоsa + с²; .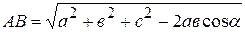

Ответ: .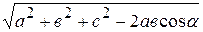

Домашнее задание: нарисовать рис. 60 стр. 48.

ВСЕ ВЫПОЛНЕННЫЕ ДОМАШНИЕ ЗАДАНИЯ СФОТОГРАФИРОВАТЬ И ПРИСЛАТЬ В VK https: //m. vk. com/id473104198