Тема урока: «Линейные уравнения и их решение»

Урок 1

Тема урока: «Линейные уравнения и их решение»

Читаем текст параграфа 6. 1. 1 и записываем определения

Уравнение− равенство, содержащее неизвестное.

Решить уравнение – это значит найти все значения входящих в него неизвестных, при которых равенство обращается в тождество. Эти значения неизвестных называют корнями уравнения.

Два уравненияравносильны, если корни первого уравнения являются корнями второго уравнения, а корни второго уравнения являются корнями первого уравнения.

Преобразование уравнения называют равносильным, если оно приводит к уравнению, равносильному данному.

1. Если к обеим частям уравнения прибавить или вычесть одно и то же число (выражение), то получим уравнение, равносильное данному. 2. Если обе части уравнения умножить или разделить на одно и то же число (выражение), отличное от нуля, то получим уравнение, равносильное данному.

Слагаемые алгебраических сумм можно переносить из одной части уравнения в другую, меняя при этом знак слагаемого на противоположный.

Линейным уравнением с одним неизвестным х называется уравнение, которое может быть представлено в виде kх + b = 0, где k, b – некоторые числа. Число k – называют коэффициентом при неизвестном, а число b – свободным членом линейного уравнения.

Алгоритм решения линейного уравнения с одним неизвестным

Решаем номера

№297 (а, е, б, в, г, д)

301(а)

310(а)

304(г)

Проверяем решение

№ 297 (а, е) а) 3х + 42 + 7х = 15х – 68 + 10; е) – 12с – 9 + 8с = 15 – 4с – 6; 3х + 7х − 15х = − 68 + 10 – 42; – 12с + 8с + 4с = − 6 + 9 + 15; − 5х = − 100; 0 ∙ с = 18; х = − 100: (− 5); нет решения х = 20 Ответ: {20} Ответ: {Æ }
№ 297 (б, в) б) – 35у + 8 + 30у = 47 – 20у – 39; − 35у + 30у + 20у = 47 – 39 – 8; 15у = 0; у = 0 Ответ: {0}	Слагаемые алгебраических сумм можно переносить из одной части уравнения в другую, меняя при этом знак слагаемого на противоположный. Записать линейное уравнение в виде kх = с, где k, с Î Q k ¹ 0, единственный корень
в) – 2z + 225 + z – 50 = 100 − z; – 2z + z + z = 100 – 225 + 50; 0 ∙ z = − 75; Нет решения Ответ: {Æ }	Слагаемые алгебраических сумм можно переносить из одной части уравнения в другую, меняя при этом знак слагаемого на противоположный. Записать линейное уравнение в виде kх = с, где k, с Î Q k = 0, с ¹ 0, нет решения

№ 297 (г, д).

г) 7а + 6 – 5а = 4 – 3а + 1 – а;

Приведём уравнение к линейному уравнению, перенесём все неизвестные в левую часть уравнения, а известные – в правую, воспользовавшись правилом переноса:

7а – 5а + 3а + а = 4 + 1 − 6;

Упростим левую и правую части уравнения:

6а = − 1;

k ¹ 0, единственный корень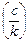

а = ;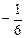

Ответ: { }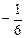

д) 10b – 24 – 2b + 18= − b + 9;

10b – 2b + b = 9 + 24 − 18;

Упростим левую и правую части уравнения:

9b= 15;

k ¹ 0, единственный корень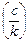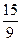

b = ;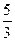

b =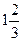

Ответ: { }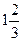

№ 301 (а)

Задание выполняется с комментарием.

а) х – (5 – х) = 3;

В левой части раскроем скобки, используя правилом раскрытия скобок, перед которыми стоит знак «− »:

х – 5 + х = 3;

Перенесём (– 5) в правую часть уравнения, меняя знак на противоположный знак, и упростим выражения в левой и правой части уравнения:

2х = 8;

k ¹ 0, единственный корень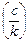

х = 8: 2;

х = 4

Ответ: {4}

№ 310 (а)

Задание выполняется с комментарием.

а) ;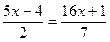

Используем свойство пропорции:

7(5х – 4) = 2(16х + 1);

Раскроем скобки, используя распределительное свойство умножения:

35х – 28 = 32х + 2;

Перенесём все неизвестные в левую часть, а известные в правую часть уравнения, применяя правила переноса:

35х – 32х = 2 + 28;

Упростим выражения в правой и левой части уравнения:

3х = 30;

k ¹ 0, единственный корень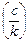

х = 30: 3;

х = 10

Ответ: {10}

№ 304 (г)

128 ч.

I II III IV

(х + 12) ч. х ч. (х + 12 + 15) ч. 2(х + 12) ч.

х > 0; х + 12 > 0; х + 27 > 0; 2(х + 12) > 0

(х + 12) + x + (х + 27) + 2(х + 12) = 128;

х + 12 + х + х + 27 + 2х + 24 = 128;

5х + 63 = 128;

5х = 128 – 63;

5х = 65;

х = 13

13 ч. – во II подъезде;

13 + 12 = 25 (ч. ) – I подъезд

13 + 27 = 40 (ч. ) – III подъезд

2 ∙ 25 = 50 (ч. ) – IV подъезд

Ответ: 25 человек, 13 человек, 40 человек, 50 человек.

№ 325

а) Если (х – 3)(х – 5) = 0, то х = 5 или х = 3 (И)

Если х = 5 или х = 3, то (х – 3)(х – 5) = 0 (И)

б) Если у² = 49, то у = 7 (И)

Если у = 7, то у² = 49 (И)

в) Если z³ = –64, то z = –4 (И)

Если z = –4, то z³ = –64 (И)

г) Если | х | > 7, то х > 7 (Л) неверно, что если | х | > 7, то х > 7

Если х > 7, то| х | > 7.

д) Если | х | £ 6, то –6 £ х £ 6 (И)

Если –6 £ х £ 6, то | х | £ 6 (И)

е) Если а > b, то b < a (И)

Если b < a, то а > b (И)

№ 329

а) x⁴ – x³ + x – 1 = (x⁴ – x³) + (x – 1) = x³(х – 1) + (x – 1) = (x – 1)(x³ + 1) =

= (x – 1)(х + 1)(х² – х + 1);

б) y³ + 27 + 7y² + 21y = (y³ + 27) + (7y² + 21y) = (у + 3)(у² – 3у + 9) + 7у(у + 3) =

= (у + 3)(у² – 3у + 9 + 7у) = (у + 3)(у² + 4у + 9);

в) z⁵ + z³ – z² – 1 = (z⁵ + z³) – (z² + 1) = z³(z² + 1) − (z² + 1) = (z² + 1)(z³ – 1) =

= (z² + 1)(z – 1)(z² + z + 1);

г) a³ – a² – 9a + 9 = (a³ – a²) – (9a – 9) = a²(а – 1) – 9(а – 1) = (а – 1)(а² – 9) =

= (а – 1)(а – 3)(а + 3);

д) b³ + 8c³ + b² – 2bc + 4c² = (b³ + 8c³) + (b² – 2bc + 4c²) =

= (b + 2с)(b² − 2bc + 4c²) + (b² – 2bc + 4c²) = (b² – 2bc + 4c²)(b + 2с + 1);

е) d³ – 4d² – 12d + 27 = (d³ + 27) – (4d² + 12d) = (d + 3)(d² − 3d + 9) − 4d (d + 3) =

= (d + 3)(d² − 3d + 9 − 4d) = (d + 3)(d² − 7d + 9);

ж) m³ – n³ – 6m² – 6mn – 6n² = (m³ – n³) – (6m² + 6mn + 6n²) =

= (m – n)(m² + mn + n²) – 6(m² + mn + n²) = (m² + mn + n²)(m – n – 6);

з) p³ – 8p² – 32p + 64 = (p³ + 64) – (8p² + 32p) = (p + 4)(p² − 4p + 16) − 8p(p + 4) =

= (p + 4)(p² − 4p + 16 − 8p) = (p + 4)(p² − 12p + 16).

Домашнее задание: п. 6. 1. 1. №№ 334 (а, в); 335 (а, б); 349 (а)