Лекция №7. Неопределенный интеграл 1.

Лекция №7. Неопределенный интеграл 1.

1. Основные понятия.

1. 1 Первообразная.

Определение.

Функция F(х) называется первообразной на некотором промежутке для функции f (х), если F´ (х) = f (х) или d F (х) = f (х)*dх.

Свойства первообразной:

1. Если функция F (х) является первообразной для функции f (х) на некотором промежутке, то множество всех первообразных для функции f (х) содержатся в выражении:

F (х) + С, где С – постоянная, С = R

2. Первообразная двух или нескольких функций равна сумме первообразных этих функций, т. е. если:

- F (х) - первообразная для функции f (х);

- G (х) - первообразная для функции g (х);

- F (х) + G (х) – есть первообразная для функции f (х) + g (х).

3. Постоянный множитель можно вынести за за знак первообразной.

4. Если функция F (х) является первообразной для функции f (х), а k и b – постояннык причем k ≠ 0, то 1 / k * F (kх + b) есть первообразная для функции f (k х + b).

2. Неопределенный интеграл.

Определение.

Неопределенным интегралом от функции f (х) или её дифференциала f (х)*dх называется совокупность всех её первообразных.

∫ f (х)dх = F (х) + С, где

- ∫ - знак интеграла;

- f (х) – подынтегральная функция;

- f (х)dх - подынтегральное выражение;

- х – переменная интегрирования.

Примечание

– отыскание неопределенного интеграла – интегрирование функции (операция обратная дифференцированию).

2. 1 Основные свойства неопределенного интеграла.

1. Неопределенный интеграл от дифференциала функции равен

этой функции плюс произвольная постоянная:

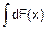=F(х)+С (1)

2. Дифференциал неопределенного интеграла равен подъинтегральному выражению, а производная неопределенного интеграла равна подъинтегральной функции:

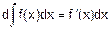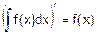, (2)

3. Неопределенный интеграл алгебраической суммы функций равен алгебраической сумме неопределенных интегралов этих функций:

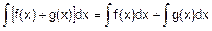(3)

4. Постоянный множитель подъинтегрального выражения можно выносить за знак интеграла неопределенного интеграла:

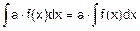(4)

2. 2 Основные формулы неопределенного интеграла (формулы нахождения первообразных - табличные интегралы).

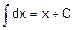
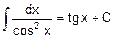
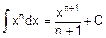
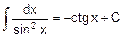
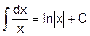
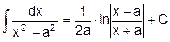
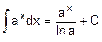
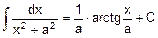
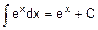
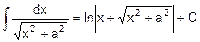
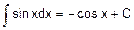
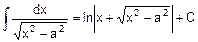
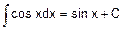
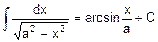
Примечание

При применении формул, содержащих знак абсолютной величины, этот знак используется в тех случаях, когда выражение, стоящее под знаком логарифма, может иметь отрицательное значение.

ДЗ:

- перенести в конспект материал лекции – обязательно таблицу основных формул неопределенного интеграла;

- контрольные вопросы:

1. Первообразная - определение.

2. Свойства первообразной – перечислить.

3. Неопределенный интеграл – определение, обозначение.

4. Основные свойства неопределенного интеграла – перечислить.