
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Ознакомьтесь с имеющимся в Единой коллекции цифровых образовательных ресурсов модулем для коллективной работы «Линейные алгоритмы» (217039). Совместно с друзьями постарайтесь составить алгоритмы для имеющихся в модуле задач. Пройдите тестирование.. 2.4.2.
Ознакомьтесь с имеющимся в Единой коллекции цифровых образовательных ресурсов модулем для коллективной работы «Линейные алгоритмы» (217039). Совместно с друзьями постарайтесь составить алгоритмы для имеющихся в модуле задач. Пройдите тестирование.
2. 4. 2. Ветвление
 Ветвление — алгоритмическая конструкция, в которой в зависимости от результата проверки условия («да» или «нет») предусмотрен выбор одной из двух последовательностей действий (ветвей). Алгоритмы, в основе которых лежит структура «ветвление», называют разветвляющимися.
Ветвление — алгоритмическая конструкция, в которой в зависимости от результата проверки условия («да» или «нет») предусмотрен выбор одной из двух последовательностей действий (ветвей). Алгоритмы, в основе которых лежит структура «ветвление», называют разветвляющимися.
Блок-схема ветвления представлена на рис. 2. 9. Каждая ветвь может быть любой степени сложности (рис. 2. 9, а), а может вообще не содержать предписаний (рис. 2. 9, б).
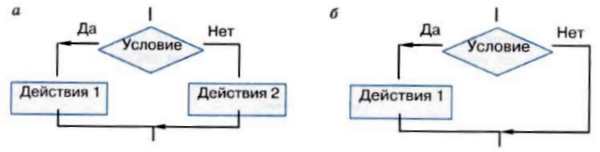
Рис. 2. 9. Структура «ветвление»: а — полная форма ветвления; б — неполная форма ветвления
На алгоритмическом языке команда ветвления записывается так:

Для записи условий, в зависимости от результатов проверки которых выбирается та или иная последовательность действий, используются операции сравнения:
А< B — А меньше В;
А< =В — А меньше или равно В;
А=B — А равно В;
А> В — А больше В;
А> =В — А больше или равно В;
А< > B — А не равно В.
Здесь буквы А и В можно заменять на любые переменные, числа и арифметические выражения. Приведённые операции сравнения допускаются и для символьных переменных.
Пример 7. Алгоритм вычисления функции f(x) = |x| для произвольного числа х.
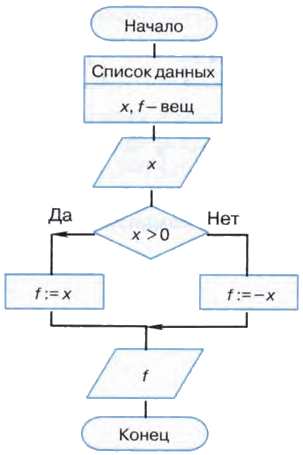
Обратите внимание на второй блок этой блок-схемы. В нём представлены имена и типы величин (данных), обрабатываемых в алгоритме.
Условия, состоящие из одной операции сравнения, называются простыми. В качестве условий при организации ветвлений можно использовать и составные условия. Составные условия получаются из простых с помощью логических связок and (и), or (или), not (не): and означает одновременное выполнение всех условий, or — выполнение хотя бы одного условия, a not означает отрицание условия, записанного за словом not.
Пример 8. Алгоритм определения принадлежности точки х отрезку [ а, b ]. Если точка х принадлежит данному отрезку, то выводится ответ ДА, в противном случае — НЕТ.
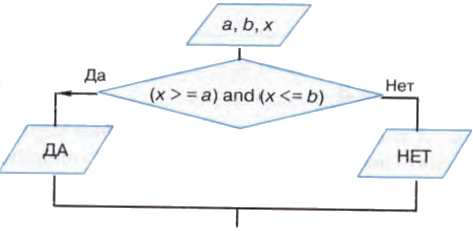
 Существует достаточно много ситуаций, в которых приходится выбирать не из двух, а из трёх и более вариантов. Есть разные способы построения соответствующих алгоритмов. Один из них — составить комбинацию из нескольких ветвлений.
Существует достаточно много ситуаций, в которых приходится выбирать не из двух, а из трёх и более вариантов. Есть разные способы построения соответствующих алгоритмов. Один из них — составить комбинацию из нескольких ветвлений.
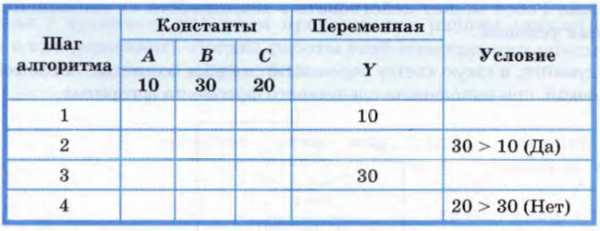
Пример 9. Алгоритм, в котором переменной У присваивается значение большей из трёх величин А, В и С.
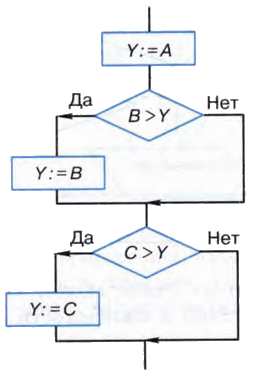
Пусть А = 10, В = 30 и С = 20. Тогда процесс выполнения алгоритма можно представить в следующей таблице:
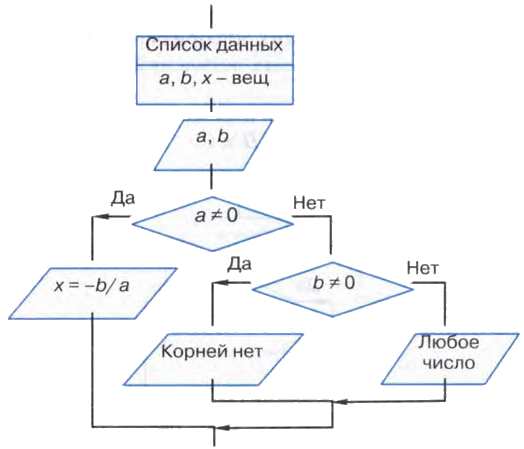
Пример 10. Алгоритм решения линейного уравнения ax + b = 0.
Пример 11. Исполнитель Робот может выполнять ту или иную последовательность действий в зависимости от выполнения следующих простых условий:

Также Робот может действовать в зависимости от выполнения составных условий.
Подумайте, в какую клетку переместится Робот из клетки, обозначенной звёздочкой, при выполнении следующего фрагмента алгоритма.

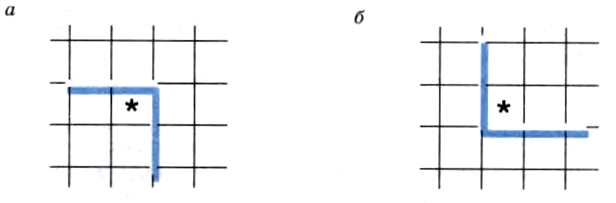
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|