Формулы для перехода от полярных координат к декартовым

⇐ ПредыдущаяСтр 2 из 2

Формулы для перехода от полярных координат к декартовым

x=ρ *cos(φ ), y=ρ *sin(φ )

и обратно:

ρ =sqrt(x²)+y²), φ =arctg(y/x)=arcsin(y/ρ )

ρ - расстояние от точки P до заданной точки O

Аффинное преобразование — отображение 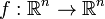, которое можно записать в виде

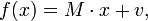
где 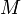— обратимая матрица и .

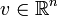Иначе говоря, преобразование называется аффинным, если его можно получить следующим образом:

1. Выбрать «новый» базис пространства с «новым» началом координат ;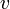

2. Каждой точке x пространства поставить в соответствие точку f(x), имеющую те же координаты относительно «новой» системы координат, что и x в «старой».

Свойства

1. При аффинном преобразовании прямая переходит в прямую.

Если размерность пространства 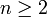, то любое преобразование пространства (то есть биекция пространства на себя), которое переводит прямые в прямые, является аффинным. Это определение используется в аксиоматическом построении аффинной геометрии

2. Частным случаем аффинных преобразований являются движения и преобразования подобия.

3. Аффинные преобразования образуют группу относительно композиции.

4. Любые три точки, не лежащие на одной прямой и их образы соответственно (не лежащие на одной прямой) однозначно задают аффинное преобразование плоскости.

Ортогональное преобразование — линейное преобразование 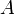евклидова пространства 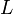, сохраняющее длины или (что эквивалентно этому) скалярное произведение векторов. Это означает, что для любых двух векторов 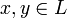выполняется равенство

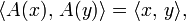
где треугольными скобками обозначено скалярное произведение 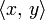в пространстве .

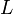Свойства

· Ортогональные преобразования (и только они) переводят один ортонормированный базис евклидова пространства в другой.

· Необходимым и достаточным условием ортогональности линейного преобразования 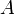является равенство

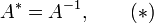
где 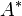— сопряжённое, а 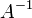— обратное преобразования.

· В ортонормированном базисе ортогональным преобразованиям (и только им) соответствуют ортогональные матрицы. Таким образом, критерием ортогональности матрицы 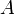является равенство равенство (*), где 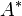— транспонированная, а 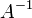— обратная матрицы.

· Собственные значения ортогональных преобразований равны по модулю 1, а собственные векторы (вообще говоря, комплексные), отвечающие различным собственным значениям, ортогональны.

· Определитель ортогонального преобразования равен 1 (собственное ортогональное преобразование) или − 1 (несобственное ортогональноепреобразование).

· В произвольном n-мерном евклидовом пространстве ортогональное преобразование является композицией конечного числа отражений.

· Множество всех ортогональных преобразований евклидова пространства образует группу относительно операции композиции — ортогональную группу данного евклидова пространства. Собственные ортогональные преобразование образуют нормальную подгруппу в этой группе (специальную ортогональную группу).

Алгебраической линией на плоскости называется множество точек, которое в какой-либо аффинной системе координат 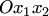может быть задано уравнением вида

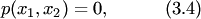
где 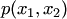— многочлен двух переменных 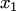и .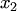

Уравнением линии называется соотношение y = f(x) между координатами точек, составляющих эту линию.

Отметим, что уравнение линии может быть выражено параметрическим способом, то есть каждая координата каждой точки выражается через некоторый независимый параметр t.

Характерный пример – траектория движущейся точки. В этом случае роль параметра играет время.

⇐ Предыдущая 12