
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
№18 ЕМТИХАН БИЛЕТІ. 1. Геометриялық сипаттамалар
№18 ЕМТИХАН БИЛЕТІ
1. Жазық қ ималардың геометриялық сипаттамалары( статикалық моменттер, екпін моменттері. )
2. Бұ ралу деформациясы.
1. Геометриялық сипаттамалар
Материалдар кедергісінде беріктік, қ атаң дық жә не орнық тылық мә селелерін
қ арастырғ анда бізге білік қ ималарының ауданынан басқ а да сипаттамалары қ ажет болады. Олар қ иманың кү рделі геометриялық сипаттамалары деп аталады.
Статикалық моменттері. Ауырлық ортасының координаталары.
Фигураның ауданының осьтерге қ атысты статикалық моменттері:
Sx = ∫ y dA, Sу = ∫ х dA
мұ ндағ ы х, у - dA- элементар ауданының Х, У осіне дейін арақ ашық тығ ы,
интеграл аудан А бойынша алынады (1-сурет). Бұ л шаманың ө лшем бірлігі,
кө бінесе см3. Бұ л шама оң, теріс таң балы жә не нө лге тең болуы мү мкін.
Бұ л шамағ а мынандай тең деу жазуғ а болады:
Sx = ∫ ydA = А∙ yc, Sу = ∫ хdA = А∙ хc
мұ ндағ ы А - фигураның толық ауданы, хc, yc - фигураның ауырлық ортасының
Х, У осіндегі координаталары.
Осы формуладан ауырлық ортасының координаталары анық талады:
Sz = yc*A, Szy= zc*A
Осы формулалардан мынандай ереже алынады:
Егер Z жә не У осьтері фигураның ауырлық орталық тарынан ө тсе, онда ол осы осьтерге қ атысты статикалық моменттер нө лге тең. Бұ л осьтерді орталық осьтер деп атайды.
Қ иманың белгілі бір оське қ арағ андағ ы статикалық моменттері сол
фигураны қ ұ райтын қ арапайым фигуралардың статикалық моменттерінің
қ осындысына тең (егер фигура бө ліктерге жіктелсе).
Қ иманың остік, полярлық жә не ортадан тепкіш екпін моменттері.
Берілген қ иманың кез келген Z, У осьтеріне қ атысты осьтік екпін моменттері деп тө мендегі интегралдармен анық талатын геометриялық сипаттамаларын айтады
Jz = ∫ y2dA, Jy = ∫ x2dA
Мұ ндағ ы z, у- dA- элементар аудан мен Z, У остерінен арақ ашық тық тары.
Берілген қ иманың полюс деп аталатын кез келген нү ктеге қ атысты ө рістік екпін моменті деп тө мендегі интегралмен анық талатын геометриялық сипаттаманы айтады:
Jρ = ∫ ρ 2dA
мұ ндағ ы ρ – полюстен шексіз кіші ауданғ а дейінгі ара қ ашық тығ ы.
Берілген қ иманың кез келген ө зара перпендикуляр Z, У осьтерге қ атысты
центрден тепкіш екпін моменті:
Jzу = ∫ zуdA
Центрден тепкіш инерция моментінің таң басы оң, теріс, кей жағ дайларда
нө лге тең болуы мү мкін. Инерция моменттерінің ө лшем бірлігі –см3
2. Бұ ралу деформациясы
Денелердің ө лшемдері мен пішіндерінің ө згеруін деформация деп атайды. Брустың В бө лігінен А қ имасы арқ ылы С бө лігіне ішкі кү штер ү здіксіз жайылып таралып беріледі (І. 6, б - сурет). Жалпы жағ дайда, бұ л ішкі кү штер қ иманың ауырлық центрі арқ ылы ө тетін, басты вектор деп аталатын R кү шіне жә не басты момент деп аталатын М моментіне келтіріледі (І. 6, в - сурет). Басты векторды OX, OY, OZ осьтерінің бойында жатқ ан 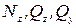 қ ұ раушы кү штеріне, ал бас моментті
қ ұ раушы кү штеріне, ал бас моментті 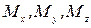 қ ұ раушы моменттеріне жіктейік. Бұ л қ ұ раушы кү штер мен моменттер ішкі кү ш компоненттері немесе факторлары деп аталады.
қ ұ раушы моменттеріне жіктейік. Бұ л қ ұ раушы кү штер мен моменттер ішкі кү ш компоненттері немесе факторлары деп аталады. 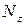 - кө лденең қ имағ а перпендикуляр бойлық ось бойымен ә сер етеді, сондық тан оны бойлық кү ш деп, ал OX, OY осьтеріне параллель ә сер ететін
- кө лденең қ имағ а перпендикуляр бойлық ось бойымен ә сер етеді, сондық тан оны бойлық кү ш деп, ал OX, OY осьтеріне параллель ә сер ететін 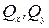 ішкі кү штерін кө лденең немесе жанама кү штер деп атайды.
ішкі кү штерін кө лденең немесе жанама кү штер деп атайды. 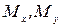 моменттерін ию, ал
моменттерін ию, ал 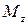 моментін бұ рау моменттері деп ажыратады.
моментін бұ рау моменттері деп ажыратады.
Сыртқ ы кү штердің ә серінен пайда болғ ан денедегі серпімді деформация дененің ө лшемдеріне қ арағ анда шексіз кіші, сондық тан, дененің бө ліктері ү шін теориялық механиканың келесі тепе – тең дік тең деулерін қ олдануғ а болады
1) 
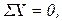
 2)
2) 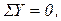 3)
3) 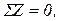
4) 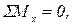 5)
5) 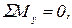 6)
6) 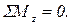 І. 03
І. 03
Бірінші ү ш тең деуден 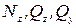 ішкі кү штері, ал соң ғ ы ү шеуінен
ішкі кү штері, ал соң ғ ы ү шеуінен 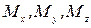 ішкі моменттері анық талады. Бұ л мысалда брусқ а ә сер ететін сыртқ ы кү штер бір жазық тық та жатпайды деп жалпы жағ дайды қ арастырдық. Енді іс жү зінде жиі кездесетін қ арапайым жағ дайларды атап ө тейік.
ішкі моменттері анық талады. Бұ л мысалда брусқ а ә сер ететін сыртқ ы кү штер бір жазық тық та жатпайды деп жалпы жағ дайды қ арастырдық. Енді іс жү зінде жиі кездесетін қ арапайым жағ дайларды атап ө тейік.
Егер дененің кез келген кө лденең қ имасында тек қ ана 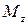 пайда болса, деформация бұ ралу деп аталады.
пайда болса, деформация бұ ралу деп аталады.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|