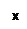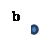- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
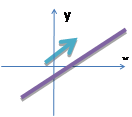
Линейная функция . График – прямая
Справочный материал к заданию ОГЭ №11. Функции и графики. №1
Линейная функция. График – прямая
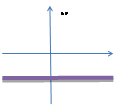
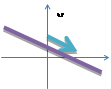
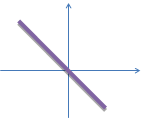
| 1) Коэффициент k | k | k=0 | k | ||||||||||||||
| функция возрастает | прямая параллельна оси Ох | функция убывает | |||||||||||||||
|
|
|
| |||||||||||||||
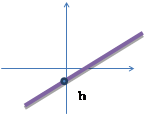
| 2) Коэффициент b
График линейной функции пересекает ось Оу в точке (0; b)
| b | b=0 | В) b | ||||||||||||||
| точка пересечения с осью Оу находится выше начала координат | прямая проходит через начало координат | точка пересечения с осью Оу находится ниже начала координат | |||||||||||||||
 
|
|
| |||||||||||||||
Справочный материал к заданию ОГЭ №11. Функции и графики. №2
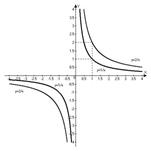
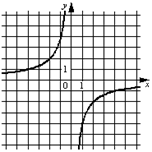
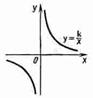
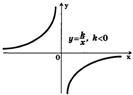
Обратная пропорциональность у= График –гипербола
| Что показывает коэффициент k? | Расположение графика |
Если рассматривать расположение двух гипербол в одной системе координат, то чем больше 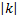 тем дальше ветви гиперболы отстоят от осей координат (около начала О). Чем меньше тем дальше ветви гиперболы отстоят от осей координат (около начала О). Чем меньше 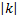 , тем ближе прилегают ветви гиперболы к осям координат (около начала О) , тем ближе прилегают ветви гиперболы к осям координат (около начала О)
| 
|
| Как найти коэффициент k? | |
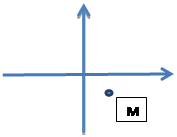
По графику всегда можно найти чему равно значение k, для этого на графике нужно взять любую точку с целочисленными координатами и подставить ее координаты в формулу у=  Например, М(-2; 2), тогда х=-2 у= 2
Подставим
Например, М(-2; 2), тогда х=-2 у= 2
Подставим
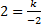 тогда k= тогда k= 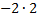 ; ; 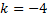 Функция имеет вид:
Функция имеет вид: 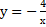
|  
|
k 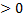
| k 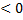
|
| ветви гиперболы в I и III четвертях | ветви гиперболы расположены в II и IV четвертях |
| 
|
Справочный материал к заданию ОГЭ №11. Функции и графики. №3
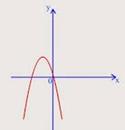
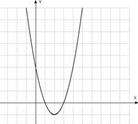
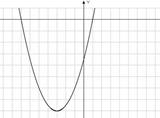
Квадратичная функция 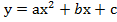 . График – парабола.
. График – парабола.
|
Коэффициент а
| а 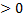
| а 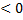
|
| ветви параболы направлены вверх | ветви параболы направлены вниз | |
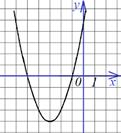
| 
| |
|
Коэффициент с Точка (0; с) – точка пересечения параболы с осью Оу
| с 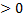
| с 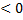
|
| Точка пересечения с осью Оу выше начала координат | Точка пересечения с осью Оу ниже начала координат | |
|   
|
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|