
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задача 1 (3 балла). Задача 2 (3 балла)
Олимпиада Университета ИТМО
по лазерной технике и лазерным технологиям
20 ноября 2014
Задача 1 (3 балла)
Определите, какая доля мощности лазерного излучения находится внутри круговой области r=2r0, где r0 - характерный размер гауссова распределения плотности мощности излучения в пучке:

Решение:
Обозначим за P(r) мощность излучения, находящуюся в круговой области радиусом r. Проинтегрируем выражение плотности мощности в полярных координатах (r, φ ):
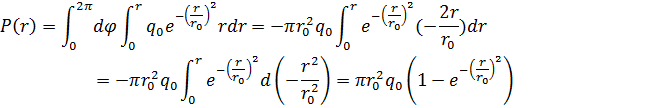
Доля мощности излучения k в круговой области радиусом r равна:
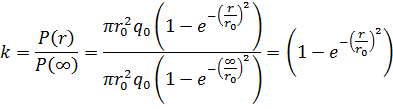
При r=2r0 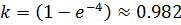
Ответ: 0. 982 или 98, 2%.
Критерии оценки:
· правильно составлен интеграл плотности мощности: +1 балл;
· правильно найдено выражение P(r): +1 балл;
· получен правильный ответ: +1 балл.
Задача 2 (3 балла)
Резонатор образован выпуклым сферическим зеркалом с радиусом кривизны R1=-1 м и вогнутым сферическим зеркалом радиусом R2=1. 5 м. Каким должно быть максимальное расстояние между зеркалами, чтобы резонатор оставался устойчивым?
Решение:
Обозначим расстояние между зеркалами резонатора как L. Далее запишем g-параметры двухзеркального резонатора: 
Критерий устойчивости: 0< g1g2< 1
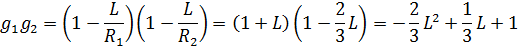
Решаем два квадратных неравенства:


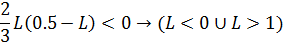
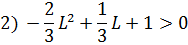
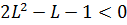
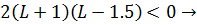
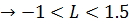
Для выполнения критерия устойчивости необходимо соблюдение обоих неравенств, откуда максимальная длина резонатора равна 1. 5 м.
Ответ: 1. 5 м.
Критерии оценки:
· записана формула g-параметра: +0. 5 балла;
· записан критерий устойчивости: +0. 5 балла;
· составлены и решены квадратные неравенства: +2 балла.
Задание 3 (4 балла)
Найдите параметры механического прерывателя, представляющего собой вращающийся диск с прорезью (размер угловой прорези φ и угловую скорость вращения диска ω ), если из импульсов длительностью τ 0=100 мкс необходимо получить импульсы излучения длительностью τ 1=40 мкс при частоте следования импульсов f=250 Гц.
Решение:
Для синхронизации вращения диска и следования импульсов лазера необходимо:
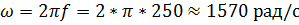
Угол φ должен соответствовать времени τ 1 при вращении диска со скоростью ω:
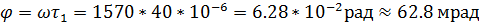
Ответ: ω =1570 рад/с; φ =62. 8 мрад.
Критерии оценки:
· верно записано выражение для ω: +1. 5 балла;
· верно записано выражение для φ: +1. 5 балла;
· рассчитано верное значение ω: +0. 5 балла;
· рассчитано верное значение φ: +0. 5 балла.
Задание 4 (4 балла)
Найдите давление паров отдачи при лазерном испарении железа, если глубина отверстия растет со скоростью Vотв=15 см/с, а скорость пара у поверхности равна Vп=1 км/с (плотность железа – 7874 кг/м3).
Решение:
Обозначим следующие величины: p – импульс отдачи, F – сила отдачи, P – давление отдачи, m – масса испаренного железа, ρ – плотность железа, h – глубина отверстия, S – площадь отверстия, V – объем испаренного железа, t – время. Напишем выражение для импульса отдачи:

Выведем выражение для давления отдачи через силу отдачи:

Ответ: 1. 18 МПа.
Критерии оценки:
· правильно записано выражение для импульса отдачи: +1 балл;
· правильно применено выражение для силы отдачи: +1 балл;
· правильно получено выражение для давления отдачи через известные величины: +1. 5 балла;
· получен верный ответ: +0. 5 балла.
Задание 5 (5 баллов)
Пучок, излучаемый Nd: YAG-лазером, имеет диаметр d=6 мм, равномерное распределение интенсивности в поперечном сечении и угол расходимости θ =3 мрад. Является ли этот пучок дифракционно-ограниченным? Оцените размер пятна ω 0 для моды ТЕМ00 резонатора.
Решение:
Обозначим следующие величины: θ d – расходимость дифракционно-ограниченного пучка, r – радиус апертуры резонатора, λ – длина волны. Формула дифракционной расходимости:
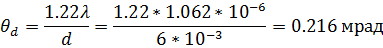
θ < θ d, следовательно, пучок не является дифракционно ограниченным.
Оценим поперечный размер основной моды:

Ответ: пучок не является дифракционно ограниченным, ω 0≈ 0. 45 мм.
Критерии оценки:
· правильно написано выражение для дифракционной расходимости: +2 балла;
· правильно написано выражение расходимости через размер пятна основной моды: +2 балла;
· сделан и обоснован верный вывод относительно дифракционной ограниченности пучка: +0. 5 балла;
· получено правильное значение размера пятна основной моды: +0. 5 балла.
Задание 6 (7 баллов)
Гауссов пучок, излучаемый гелий-неоновым лазером видимого диапазона, имеющий размер пятна в перетяжке ω 01=0, 5 мм, нужно сфокусировать таким образом, чтобы перетяжка пучка с размером пятна ω 02=50 мкм образовалась на расстоянии 1 м от перетяжки исходного пучка. Какое фокусное расстояние должна иметь линза и где она должна быть расположена?
Решение:
Обозначим следующие величины: L=1 м – расстояние между перетяжками, L1 – расстояние от перетяжки исходного пучка до линзы, L2=L-L1 – расстояние от линзы до перетяжки полученного пучка, f – фокусное расстояние линзы, λ – длина волны. Для расчета применим метод ABCD-матриц.
Матрица воздушного промежутка длиной L1: 
Матрица тонкой линзы с фокусным расстоянием f: 
Разобьем нашу систему последовательно на воздушный промежуток длиной L1, тонкую линзу с фокусным расстоянием f и воздушный промежуток длиной L2. По правилам матричной оптики, для того, чтобы получить матрицу системы элементов, необходимо перемножить матрицы элементов в обратном порядке. Отсюда найдем матрицу искомой системы:
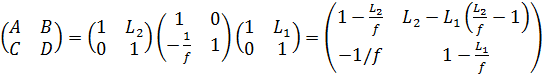 (1)
(1)
Комплексные параметры пучков q1 и q2 в плоскостях перетяжек связаны соотношением:
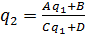 (2)
(2)
Общая формула комплексного параметра гауссова пучка:
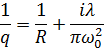
где R – радиус кривизны волнового фронта. Волновой фронт в перетяжке является плоским, значит, R=∞, 1/R=0. Отсюда выразим комплексные параметры:
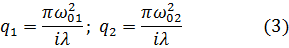
Подставим (1) и (3) в (2), получим:

Приравнивая действительные и мнимые части, получаем систему уравнений:

Заменим L2=L-L1=1-L1 и решим полученную систему уравнений для двух неизвестных – L1 и f.
Ответ: f≈ 14. 3 см; L1=85 см.
Критерии оценки:
· записаны матрицы элементов: +1 балл;
· получена матрица системы: +1 балл;
· записана формула комплексного параметра: +1 балл;
· записано выражение связи комплексных параметров: +1 балл
· получена система уравнений: +1. 5 балла;
· получен верный ответ: +1. 5 балла.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|