Контакты

Случайная статья

3.2. Преобразование КС-грамматики с ε-правилами в эквивалентную НКС-грамматику

⇐ ПредыдущаяСтр 2 из 2

3. 2. Преобразование КС-грамматики с ε -правилами в эквивалентную НКС-грамматику

Преобразуем грамматику 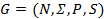, где , ,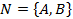

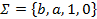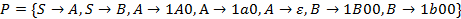в НКС-грамматику.

В нашей грамматике есть правило 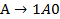и 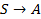, заменим A на 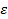, получим

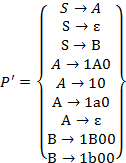
Теперь исключим из множества P’ все правила вида :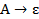

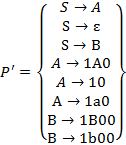
В нашей грамматике есть правило 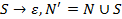. Добавим в 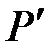два правила: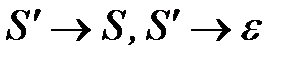

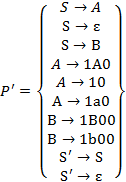
Теперь исключим из множества P’ все правила вида 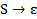, получим

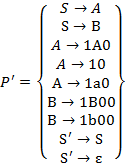
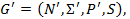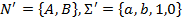Получаем искомую НКС-грамматику где и

.

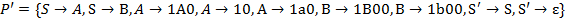3. 3. Исключение цепных правил

Удалим в грамматик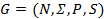е , где , ,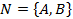

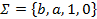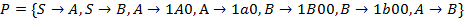цепные правила.

ДляS, A, B определяем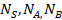

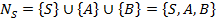
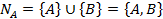
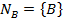
Для 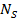в множество берем P’

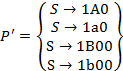
Для 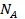в множество берем P’

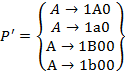
Для 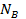в множество берем P’

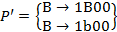
Окончательно получаем

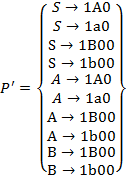
3. 4. Удаление произвольного правила вывода

Удалим в грамматик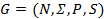е , где , ,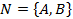

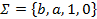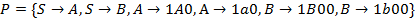произвольное правило вывода по алгоритму.

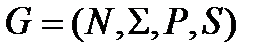
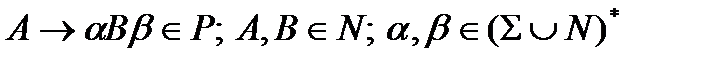
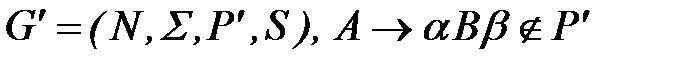
Удалим правило .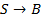

Находим в грамматике правила: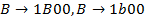

Строим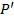

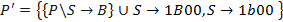
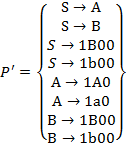
3. 5. Устранение прямой левой рекурсии

Устраним в грамматик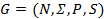е , где , ,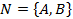

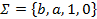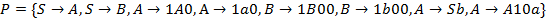прямую левую рекурсию по алгоритму.

Пусть имеется множество нетерминалов .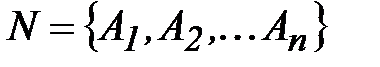

for 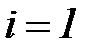to n do

.

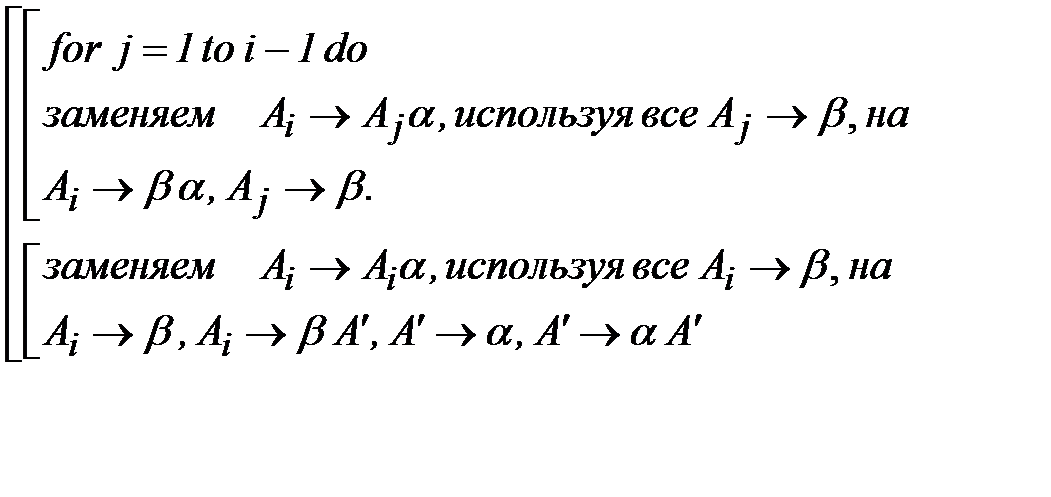
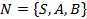Введем обозначения А₁=S, А₂=A, А₃=B

i=1, цикл по j пропускаем т. к. он до 0.

Правила вида 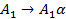в грамматике нет, поэтому i=2, j=1.

Ищем правила вида 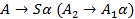- 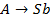, значит .

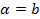Используем все правила 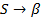: 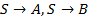, значит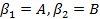

Заменим 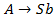на 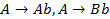, получим:

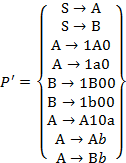
Ищем правила вида 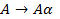- 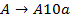, , 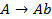значит .

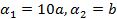Используем все правила 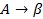: 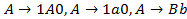, значит

.

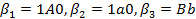Заменим 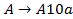, 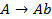на

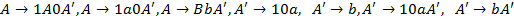
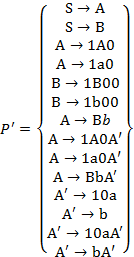
i=3, j=1. Правила вида 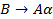в грамматике нет, поэтому i=3, j=2.

Правила вида 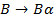в грамматике нет.

Окончательно получаем:

⇐ Предыдущая 12

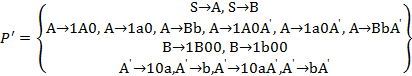
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.