Тема 3.2. Выборочный метод в статистических исследованиях

Семинарское / практическое занятие № 6 [1]

Тема 3. 2. Выборочный метод в статистических исследованиях

Перечень вопросов для подготовки к семинарскому занятию:

1. Понятие о выборочном методе исследования, его значение и задачи. Условия применения выборочного метода в Статистике.

2. Теоретические основы выборочного метода.

3. Этапы выборочного исследования. Ошибка выборки.

4. Определение оптимальной численности выборки. Малая выборка.

5. Способы распространения характеристик выборки на генеральную совокупность.

Примеры решения практических задач:

Задача 1

Требуется рассчитать предельную ошибку выборки для уровня доверительной вероятности 0, 9545, если генеральную совокупность составляют 4000 уголовных дел на преступления, совершенные в стране за месяц, а изучаемым признаком является срок расследования преступления, фиксируемый в сутках. Объем произведенной бесповторной выборки составил 200 ед. При этом известно, что средняя арифметическая вариантов изучаемого признака по данной выборке (x ̃ ) составляет 56 сут, а значение оценки генеральной дисперсии (S²) равно 64.

Таблица 1. Соотношение уровня доверительной вероятности и коэффициента доверия

Коэффициент доверия t	1, 0	1, 96	2, 0	2, 58	3, 0
Уровень доверительной вероятности р	0, 6827	0, 9500	0, 9545	0, 9901	0, 9973

Решение:

Поскольку заданный уровень доверительной вероятности по табл. 1 соответствует коэффициенту доверия t, равному 2, то, подставляя имеющиеся данные в соответствующую формулу, получим

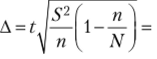
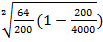= = 0, 5 (сут)

Это означает, что средняя величина изучаемого признака (средний срок расследования преступления), рассчитанная по выборке (выборочная средняя), составляющая в нашем примере 56 сут, может отклониться от средней, рассчитанной по генеральной совокупности (генеральной средней), не более чем на ±0, 5 сут с вероятностью 0, 9545 (т. е. можно утверждать, что если бы мы рассчитали среднюю величину по всей генеральной совокупности, то ее значение находилось бы с указанной вероятностью в пределах от 55, 5 до 56, 5 сут).

Задача 2

Произвести расчет необходимого объема выборки на примере той же совокупности, что и при расчете ошибки репрезентативности, т. е. при: N (объем генеральной совокупности) составляет 4000 преступлений, изучаемым признаком является срок расследования преступления, а значение оценки генеральной дисперсии (S²) равно 64. При этом в соответствии с целями нашего наблюдения предельная ошибка выборки не должна превышать ±1 сут с вероятностью 0, 9545. Таким образом, Δ = 1, a t = 2 (в соответствии с табл. 1).

Решение:

Допустим, что для формирования выборочной совокупности был использован бесповторный метод. Тогда, подставляя указанные исходные данные в соответствующую формулу, получим

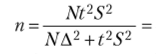
n = (4000× 2²× 64)/(4000× 1 + 2²× 64) = 1024000/4256 = 241 ед.

Таким образом, если из имеющихся 4000 ед. мы выберем для наблюдения 241 ед. и рассчитаем по данной выборке среднее значение изучаемого признака (срок расследования преступления), то с вероятностью 0, 9545 можно будет утверждать, что это значение отклонится от генеральной средней не более чем на ±1 сут.

Если же такая точность необязательна и при том же уровне доверительной вероятности нас устроит предельная ошибка, например ±2 сут (Δ = 2), то необходимый объем выборки будет значительно меньше:

n = (4000× 2²× 64)/(4000× 4 + 4× 64) = 1024000/16256 = 63 ед.

Необходимый объем выборки также сильно зависит и от выбранного уровня доверительной вероятности.

Задача 3

Для определения среднего возраста 100 тыс. человек, совершивших экономические преступления в России, необходимо провести выборочное обследование методом механического отбора. При проведении предыдущего подобного обследования величина дисперсии составила 75. Определить необходимую численность выборки, чтобы с вероятностью 0, 997 предельная ошибка выборки не превышала бы 2, 5 года.

Решение:

Под выборочным методом понимается метод статистического исследования, при котором обобщающие характеристики всей совокупности устанавливаются по некоторой ее части отобранной в случайном порядке.

Определим численность выборки по формуле:

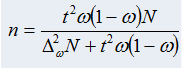
Предварительно находим по приложению значение t, соответствующее доверительной вероятности 0, 997.

t = 3

n = (3² × 0, 75 (1 – 0, 75)× 100000)/(2, 5² × 100000 + 3² × 0, 75 (1 – 0, 75)) = 27 чел.

Перечень рекомендуемой литературы для подготовки к семинарскому занятию:

1. Сергеева И. И. Статистика: учебник / И. И. Сергеева, Т. А. Чекулина, С. А. Тимофеева. - 2-e изд., испр. и доп. - М.: ИД ФОРУМ: НИЦ ИНФРА-М, 2016. - 304 с. - (Профессиональное образование).

2. Гладун И. В. Статистика: учебник. — М.: КноРус, 2016. — 232 с. — (Среднее профессиональное образование).

3. Мусина Е. М. Статистика. Краткий курс лекций и тестовые задания: учебное пособие. - 2-e изд., перераб. и доп. - М.: Форум: НИЦ ИНФРА-М, 2015. - 72 с. - (Профессиональное образование).

4. Правовая статистика: учебник и практикум для СПО/ под общ. ред. Л. К. Савюка. — М.: Юрайт, 2018. — 410 с. — (Профессиональное образование).

5. Андрюшечкина И. Н. Судебная статистика: учебное пособие/ И. Н. Андрюшечкина. - М.: РГУП, 2016. - 273с.

6. Сайт Судебного департамента при ВС РФ: http: //www. cdep. ru

[1] ответы на задание необходимо предоставить не позднее 3 рабочих дней после даты проведения семинарского/практического задания по текущей теме