1. Установление цели эксперимента

Анализ размерности (англ. Dimensional analysis — «размерный анализ» или «пространственное изучение»; чаще говорят «соображения размерности» или «метрические соображения») — инструмент, используемый в физике, химии, технике и нескольких направлениях экономики для построения обоснованных гипотез о взаимосвязи различных параметров сложной системы.

Суть метода в простейшем случае заключается в том, что для поиска выражения одного из параметров исследуемой системы через другие из последних составляется формула (их произведение в каких-то степенях), имеющая нужную размерность; часто именно она и оказывается искомым соотношением (с точностью до безразмерного множителя).

Простейший пример: если обозначить размерности физической величины буквами M, L, T, и поставить им в соответствие массу, расстояние, время, то такая физическая величина, как скорость, может быть представлена как «расстояние / время», то есть как (L/T), а сила может быть представлена как «масса × ускорение» или «масса × расстояние/время² » или (ML/T² ).

С помощью таких же соотношений можно выразить мощность, импульс и другие величины, в том числе весьма необычные, такие, как «вязкость» или «скорость переноса мощности»

Основные единицы: килограмм, метр, секунда, ампер, кельвин, моль и кандела.

Производные единицы получаются из основных с помощью алгебраических действий, таких как умножение и деление.

пример представление производных единиц: мощность - Дж/с = кг·м²·c^{− 3}

32.

ФУНКЦИОНАЛЬНЫЕ МОДЕЛИ [functional models] — один из двух основных типов математической модели (при её классификации по способам выражения соотношений между внешними условиями, внутренними параметрами и искомыми характеристиками моделируемого объекта) наряду со структурными моделями. Ф. м. описывает поведение системы безотносительно к ее внутренней структуре. Если обозначить входы и выходы моделируемого объекта соответственно через X и Y, то построить Ф. м. — это значит отыскать оператор D, связывающий X и Y, т. е. Y=D(X).

При изучении Ф. м. возникают гипотезы о причинах тех или иных реакций объекта на воздействие внешней среды и, таким образом, открывается путь к анализу его структуры и формированию структурных моделей.

33. \35.

Критерий подобия(безразмерные комплексы) — безразмерная величина, составленная из размерных физических параметров, определяющих рассматриваемое физическое явление. Равенство всех однотипных критериев подобия для двух физических явлений и систем — необходимое и достаточное условие физического подобия этих систем.

Критерии подобия, представляющие собой отношения одноимённых физических параметров системы (например, отношения длин), называются тривиальными и при установлении определяющих критериев подобия обычно не рассматриваются: равенство их для двух систем является определением физического подобия. Нетривиальные безразмерные комбинации, которые можно составить из определяющих параметров, и представляют собой критерии подобия.

Например:

«Из каждых 10 яблок 1 гнилое» — отношение количества гнилых яблок к собранным (1 яблоко)/(10 яблок) = 0, 1 = 10 %, и является тривиальным безразмерным числом.

Всякая новая комбинация из критериев подобия также является критерием подобия, что даёт возможность в каждом конкретном случае выбрать наиболее удобные и характерные критерии. Число определяющих нетривиальных критериев подобия меньше числа определяющих физических параметров с различными размерностями на величину, равную числу определяющих параметров с независимыми размерностями.

Если известны уравнения, описывающие рассматриваемое физическое явление, то критерии подобия для этого явления можно получить, приводя уравнения к безразмерному виду путём введения некоторых характерных значений для каждого из определяющих физических параметров, входящих в систему уравнений. Тогда критерии подобия определятся как безразмерные коэффициенты, появляющиеся перед некоторыми из членов новой, безразмерной системы уравнений. Когда уравнения, описывающие физическое явление, неизвестны, критерии подобия отыскиваются при помощи анализа размерностей, определяющих физические параметры.

Под математической моделью понимают уравнение, связывающее параметр оптимизации с факторами, т. е. y = f (x₁, x₂, …x_k).

36\43

План проведения эксперементальных исследований

1. Установление цели эксперимента

2. Уточнение условий проведения эксперимента (имеющееся или доступное оборудование, сроки работ, финансовые ресурсы, численность и кадровый состав работников и т. п. ). Выбор вида испытаний (нормальные, ускоренные, сокращенные в условиях лаборатории, на стенде, полигонные, натурные или эксплуатационные).

3. Выявление и выбор входных и выходных параметров на основе сбора и анализа предварительной (априорной) информации.

4. Установление потребной точности результатов измерений (выходных параметров), области возможного изменения входных параметров, уточнение видов воздействий. Выбирается вид образцов или исследуемых объектов, учитывая степень их соответствия реальному изделию по состоянию, устройству, форме, размерам и другим характеристикам.

5. Составление плана и проведение эксперимента — количество и порядок испытаний, способ сбора, хранения и документирования данных.

6. Статистическая обработка результатов эксперимента, построение математической модели поведения исследуемых характеристик.

7. Объяснение полученных результатов и формулирование рекомендаций по их использованию, уточнению методики проведения эксперимента.

Матрица планирования

№ опыта	х₀	х₁	х₂	х₃= х₁х₂	у_СР
	+	-	-	+	у₁
	+	+	-	-	у₂
	+	-	+	-	у₃
	+	+	+	+	у₄

Условия эксперимента представляются в виде таблицы – матрицы планирования, где строки соответствуют различным опытам, а столбцы – значениям факторов.

37.

Экспериме́ нт (от лат. experimentum — проба, опыт), также опыт, в научном методе — метод исследования некоторого явления в управляемых условиях. Отличается от наблюдения активным взаимодействием с изучаемым объектом. Обычно эксперимент проводится в рамках научного исследования и служит для проверки гипотезы, установления причинных связей между феноменами.

Эксперимент — это метод исследования, который воспроизводится в описанных условиях неограниченное количество раз, и даёт идентичный результат.

Измерительно-информационный комплекс(система) - комплекс измерительных устройств, обеспечивающих одновременное получение человеком-оператором или ЭВМ необходимой информации о свойствах и состоянии какого-либо объекта. Объекты измерения часто имеют весьма сложное устройство и в них могут происходить многогранные процессы и явления, поэтому отдельные измерительные устройства, воспринимающие лишь один параметр сложного процесса, обычно не могут обеспечить получение достаточной информации об объекте, особенно когда нужно одновременно знать ряд его параметров. Это необходимо, например, для управления электростанцией, доменной печью, самолётом или автомобилем, когда требуется одновременный анализ нескольких десятков, иногда сотен величин, характеризующих состояние этих объектов. Задача, решаемая ИИС, в какой-то мере обратна задаче отдельного измерительного устройства: не расчленять параметры объекта измерения с целью выделить и воспринять их по отдельности, а объединить данные о всех главных параметрах объекта и создать тем самым достаточно полное, совокупное его описание.

38.

В науке и искусстве идеей называется главная мысль произведения или общий принцип теории или изобретения, вообще замысел или наиболее существенная часть замысла. В этом же смысле термин идея трактуется в сфере регулирования авторского права.

39. \41.

чем больше факторов будет включено в модель, тем точнее будет модель. Однако, тем больше потребуется трудозатрат на оценивание модели. С другой стороны, при малом числе факторов в модели ее оценивание требует меньше трудозатрат, но точность модели мала.

Теоретически, проверка адекватности модели возможна лишь при реализации активного эксперимента. Однако, оценка работоспособности (т. е. определение характеристик точности) модели возможна всегда. Если модель неадекватна, или не удовлетворяет исследователя по работоспособности, то необходимо возвратиться к этапу 2 процедуры построения модели, выдвинуть альтернативную гипотезу о структуре модели и повторить все остальные этапы процедуры. Построение модели заканчивается либо при положительном исходе проверки адекватности, либо при удовлетворительной работоспособности.

На исследуемый объект воздействуют четыре группы параметров:

1. X = (x₁, x₂, …x_k) – контролируемые и управляемые параметры, допускающие целенаправленное изменение в ходе исследования.

Их называют независимыми параметрами.

2. U = (u₁, u₂, …u_i) - контролируемые параметры, не допускающие целенаправленного изменения в ходе исследования. К ним можно отнести условия окружающей среды.

3. Z = (z₁, z₂, …z_m) - неконтролируемые и неуправляемые параметры. Они характеризуют возмущения, которые нельзя измерить количественно (например, старение деталей).

4. Y = (y₁, y₂, …y_n) - выходные параметры.

42.

Семанти́ ческая сеть(модель) — информационная модель предметной области, имеющая вид ориентированного графа, вершины которого соответствуют объектам предметной области, а дуги (рёбра) задают отношения между ними. Объектами могут быть понятия, события, свойства, процессы^[1]. Таким образом, семантическая сеть является одним из способов представления знаний.

Дробный факторный эксперимент

В полном факторном эксперименте разность между числом опытов и коэффициентов уравнения регрессии велика. Количество опытов в ПФЭ типа 2^k при 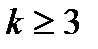значительно превышает число линейных коэффициентов. Было бы заманчивым сократить число опытов за счет той информации, которая не существенна при построении линейных моделей. При этом нужно стремиться к тому, чтобы матрица планирования не лишилась своих оптимальных свойств.

Обратимся вновь к ПФЭ типа 2³. Пользуясь таким планированием, можно вычислить семь коэффициента: b₀, b₁, b₂, b₃, b₁₂, b₂₃, b₁₃

Если имеются основания считать, что в выбранных интервалах варьирования процесс описывается линейной моделью

y = b₀ + b₁x₁ + b₂x₂+ b₃x₃,

то достаточно определить четыре коэффициента: b₀, b_1, b₂, b₃. Тогда вектор – столбец, например х₁х₂, можно использовать для введения в план нового вектора х₃. Итак, мы нашли способ сократить число опытов. Вместо восьми опытов для трёх факторов при ПФЭ типа 2³ оказывается можно поставить только четыре опыта, воспользовавшись дробным планированием или дробной репликой ½ - репликой для 2³.

P. S. это самое простое и подробное определение которое нашёл))

Линейное программирование — математическая дисциплина, посвящённая теории и методам решения экстремальных задач на множествах 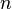-мерного векторного пространства, задаваемых системами линейных уравнений и неравенств.

Линейное программирование является частным случаем выпуклого программирования, которое в свою очередь является частным случаем математического программирования. Одновременно оно — основа нескольких методов решения задач целочисленного и нелинейного программирования. Одним из обобщений линейного программирования является дробно-линейное программирование.