Хелпикс

Главная

Контакты

Случайная статья



Разбор решения нулевого варианта (часть первая)



Привожу решение задач нулевого варианта контрольной работы. Напоминаю, что ответ по теме Ряды считается полным только если указано по какому признаку ряд сходится (условно или абсолютно) или расходится.

 

Задание 1. Вычислить площадь фигуры, ограниченной линиями: , ,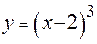

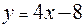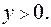
Решение: Картинку нарисуйте сами.

 

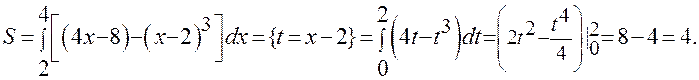
Задание 2. Вычислить несобственный интеграл .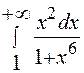

Решение:

 

 

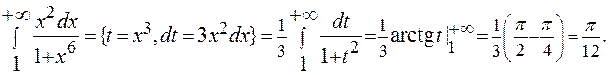
Задание 3. Исследовать на абсолютную и условную сходимость знакопеременный ряд. Указать используемый признак сходимости:

а) ,              б) .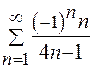

Решение: а) Ряд  знакочередующийся. Он, конечно, сходится по признаку Лейбница. Но он также абсолютно сходится (первый признак сравнения для знакопеременных рядов). Сравнение с рядом 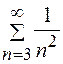, поскольку  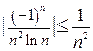при 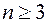 (так как тогда ).

 

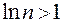б) Ряд 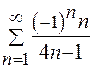расходится по необходимому условию сходимости, так как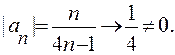

Задание 4. Найти объем тела, образованного при вращении кривой вокруг оси : .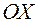

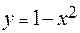
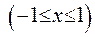Решение: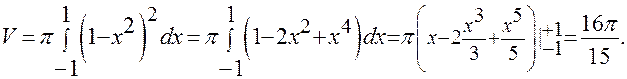     

Задание 5. Исследовать на сходимость несобственный интеграл: .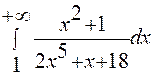

Решение:

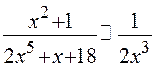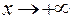 при . Но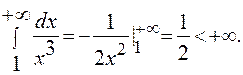

 

Следовательно, несобственный интеграл сходится по второму признаку сравнения.

Но можно и по первому признаку сравнения, поскольку справедливо неравенство:

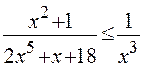 при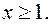

Задание 6. Исследовать на сходимость ряд с положительными членами. Указать используемый признак сходимости:

а) 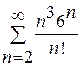,              б) .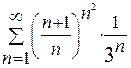

 

Решение: а) Ряд 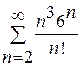 сходится по признаку Даламбера, поскольку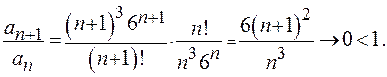

б) Ряд 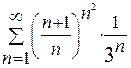 сходится по радикальному признаку Коши, поскольку 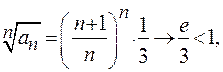в силу второго замечательного предела.

 

 



  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.