
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Практическое занятие: Решение простейших тригонометрических уравнений
Практическое занятие: Решение простейших тригонометрических уравнений
Цель: закрепитьнавыки решения простейших тригонометрических уравнений на конкретных примерах.
Оборудование: тетрадь для практических работ, ручка, карандаш, методические рекомендации по выполнению работы
Указание. Практическая работа состоит из двух частей – теоретической и практической (задания для самостоятельного выполнения). После изучения теоретического материала можно приступать к выполнению практической части.
Порядок выполнения работы.
1. Рассмотрите теоретический материал по теме и примеры решения задач (приведены ниже).
2. Решите самостоятельную работу. Оформите решение письменно в тетради.
Ход работы.
Теоретический материал.
Сводная таблица решения простейших тригонометрических уравнений
| Уравнение | Общее решение | |
| sinx=a | 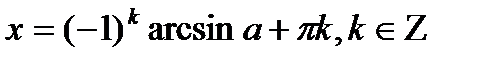
| |
| cosx=a | 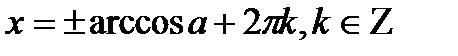
| |
| tgx=a | 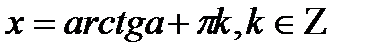
| |
| ctgx=a | 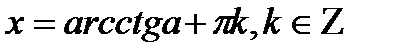
|
Частные случаи решения простейших тригонометрических уравнений
| Уравнение | Частные случаи | ||
| а=-1 | а=0 | а=1 | |
| sinx=a | 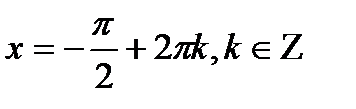
| 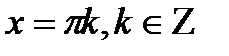
| 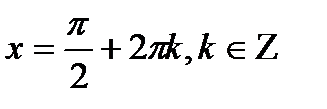
|
| cosx=a | 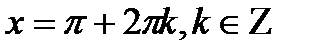
| 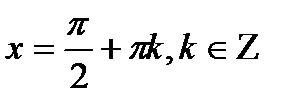
| 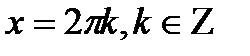
|
| tgx=a | 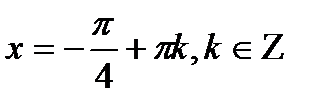
| 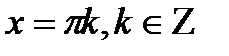
| 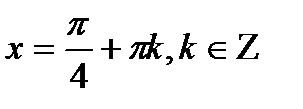
|
| ctgx=a | 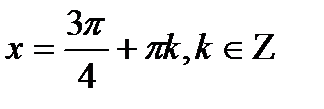
| 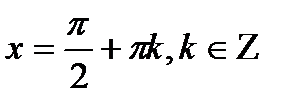
| 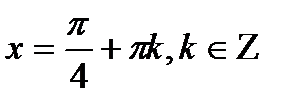
|
Пример 1. Решите уравнение: sin t= 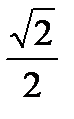 . Найдите корни, принадлежащие промежутку
. Найдите корни, принадлежащие промежутку 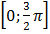
Решение: по формуле t=(-1)karсsin ( 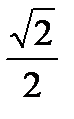 )+π k, (k Є Z ). Поскольку arсsin (
)+π k, (k Є Z ). Поскольку arсsin ( 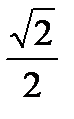 )=π /4 приходим к ответу t=(-1)k π /4+π k, (k Є Z ).
)=π /4 приходим к ответу t=(-1)k π /4+π k, (k Є Z ).
Если k=0, то t = π /4 Є 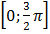 ; k=-1, t=(-1)-1π /4+π (-1)= -5 π /4 не принадлежит промежутку, k=1, t=(-1)1π /4+π (1)= -π /4 + π =3 π /4 Є
; k=-1, t=(-1)-1π /4+π (-1)= -5 π /4 не принадлежит промежутку, k=1, t=(-1)1π /4+π (1)= -π /4 + π =3 π /4 Є 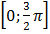 , k=2, t=(-1)2π /4+π (2)= π /4 + 2π =9 π /4 не принадлежит промежутку.
, k=2, t=(-1)2π /4+π (2)= π /4 + 2π =9 π /4 не принадлежит промежутку.
Ответ: π /4; 3 π /4
Пример 2. Решите уравнение: cos (2х-π /4)=1/2.
Решение: по формуле 2х-π /4=±arсcos (1/2)+2π n, (n Є Z ). Поскольку arсcos (1/2)=π /3 получаем 2х-π /4=± π /3+2π n, (n Є Z ); 2х=π /4± π /3+2π n, (n Є Z ).
Разделив обе части уравнения на 2 получим ответ: х=π /8±π /6+π n, (nЄ Z ).
Задания для самостоятельного решения:
1. Решить уравнения.
а) cos x= 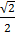 ; б) sin(x-
; б) sin(x- 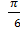 ) = -1; в) tgx -
) = -1; в) tgx -  =0; г) 2 sin x cosх = -1;
=0; г) 2 sin x cosх = -1;
д) cos 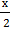 -1=0; е)2сtgx+2=0
-1=0; е)2сtgx+2=0
2. Найдите корни уравнения, которые принадлежат промежутку 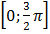
а) sin 2x=  ; б) tg (x+
; б) tg (x+ 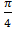 )=-1
)=-1
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|