Урок9 КОМ-21. Тема. Степень с рациональным показателем. 1. Прочитать конспект.. 2. Записать определение и разбор примеров, которые выделены цветом.. 3. Решить задание, выделенное синим № 3. Если m>n, то аm>аn при а>1 и аm<аn при 0<а<1..

Урок9 КОМ-21

Тема. Степень с рациональным показателем

ПЛАН.

1. Прочитать конспект.

2. Записать определение и разбор примеров, которые выделены цветом.

3. Решить задание, выделенное синим № 3

Ранее было определено понятие степени с целым показателем. Выражение аⁿ определено для всех а и n, кроме случая а=0 при n≤ 0. Напомним свойства этих степеней:

Для любых чисел а, b и любых целых чисел m и п справедливы равенства:

1. a^m*aⁿ=a^m+n;

2. a^m: аⁿ=a^m-n (а≠ 0);

3. (а^m)ⁿ = а^mn;

4. (ab) ⁿ = aⁿ*bⁿ;

5. 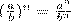(b≠ 0);

6. а¹=а; а⁰=1 (а≠ 0).

Отметим также следующее свойство:

Если m> n, то аm> аn при а> 1 и аm< аn при 0< а< 1.

В этом разделе мы обобщим понятие степени числа, придав смысл выражениям типа 2^{0. 3}, 8^5/7, 4^-1/2 и т. Д

Определение. ЗАПИСАТЬ

Степенью числа а> 0 с рациональным показателем r= 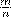, где m — целое число, а n — натуральное (n > 1), называется число

Например:

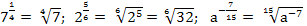
При этом степень числа 0 определена только для положительных показателей.

Сделаем ряд замечаний, связанных с понятием степени с рациональным показателем.

Замечание 1.

Из определения степени с рациональным показателем сразу следует, что для любого положительного а и любого рационального r число a^r положительно.
Замечание 2.

Любое рациональное число допускает различные записи его в виде дроби, поскольку для любого натурального k. Значение a^r также не зависит от формы записи рационального числа r. В самом деле, из свойств корней следует, что

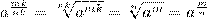
Замечание 3.

При а < 0 рациональная степень числа а не определяется, и это не случайно, например, значение 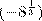равнялось бы 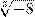, т. е. — 2. Но, с другой стороны, , и поэтому должно выполняться равенство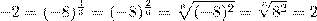

Для степеней с рациональным показателем сохраняются основные свойства степеней, верные для любых показателей (при условии, что основание степени будет положительным).

1. ;

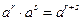2. ;

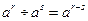3. ;

4. ;

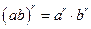5. ;

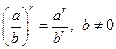6. если ;

7. если .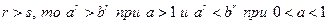

Закрепим теоретический материал при решении примеров.

12 Следующая ⇒