
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задачи к разделу «ЭНТРОПИЯ». Решение.. Решение.. Решение.
Задачи к разделу «ЭНТРОПИЯ»
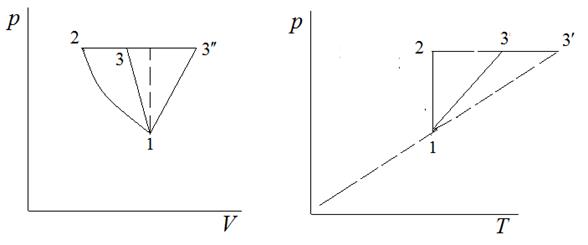
Задача № 1. 2 моль идеального двухатомного газа, находящегося при 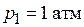 и
и 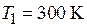 были задействованы в следующем циклическом процессе, все стадии которого обратимы
были задействованы в следующем циклическом процессе, все стадии которого обратимы
1) изотермическое сжатие до 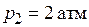 ,
,
2) изобарическое нагревание до 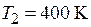 ,
,
3) возвращение в исходное состояние.
Изобразите указанный процесс на  и
и 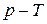 диаграммах и вычислите
диаграммах и вычислите 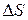 для каждой стадии цикла.
для каждой стадии цикла.
Решение.
1. Построение зависимостей 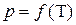 и
и 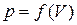
1.  .
. 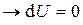
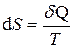
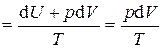
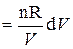 ;
;
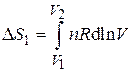
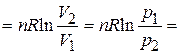
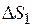 =
=
2. 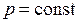 ,
, 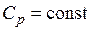
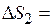
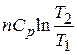
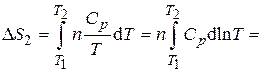
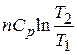
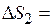
3.
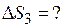 –
– 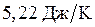
Задача № 2. 3 моль идеального двухатомного газа сначала обратимо и изотермически расширяют до 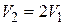 , а затем при
, а затем при 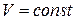 повышают температуру в
повышают температуру в 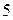 раз. Определите
раз. Определите 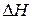 и
и 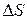 для суммарного процесса.
для суммарного процесса.
Решение.
Поскольку энтропия есть т/д функция состояния, то ее изменение в суммарном процессе будет равно сумме изменения энтропии в указанных двух последовательных стадиях процесса
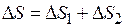 =?
=?
Задача № 3. На основании справочных данных о зависимости теплоемкости от температуры рассчитайте изменение энтропии при нагревании 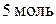 метана от
метана от 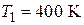 до
до 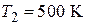 .
.
Решение.
1. Уравнение для расчета изменения энтропии будет аналогично использованному в 1-ой задаче (п. 2):
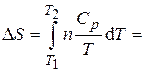 ,
,
Но в данном случае 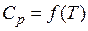
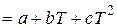 .
.
Тогда
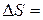
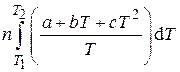
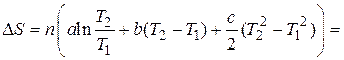
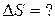
Задача № 4. Найдите изменение энтропии 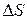 при образовании 1 моль воздуха при
при образовании 1 моль воздуха при 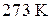 . Азот и кислород считать идеальными газами, Состав воздуха
. Азот и кислород считать идеальными газами, Состав воздуха 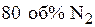 (1) и
(1) и 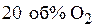 (2), каждый газ изначально находился при
(2), каждый газ изначально находился при 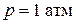 .
.
Решение.
1. При смешении идеальных газов изменения температуры не происходит, т. е. процесс идет при 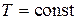 . Очевидно, также, что после смешения каждый из газов (и азот, и кислород) будут находиться под давлением
. Очевидно, также, что после смешения каждый из газов (и азот, и кислород) будут находиться под давлением 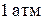 .
.
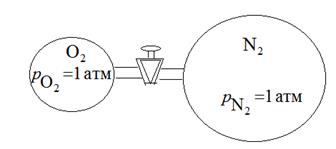
Изменение энтропии (функция состояния) при смешении равно сумме изменения энтропии каждого газа в отдельности:
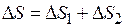 , где
, где 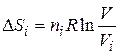 (задача 1, п. 1)
(задача 1, п. 1)
Суммарный объем газов после смешения 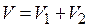 .
.
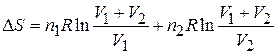
2. Найдем число моль и объемы каждого газа.
а) Для идеального газа мольная доля в смеси идеальных газов равна его объемной доле 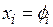 .
.
Так, например, для 1-го газа ( 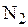 ):
):
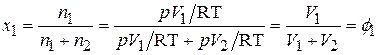
Откуда
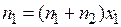
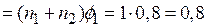
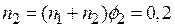
б) Объем каждого газа найдем по уравнению Менделеева-Клапейрона, 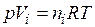 :
:
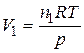
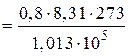
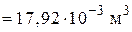
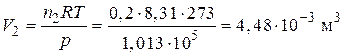
в) Находим изменение энтропии при смешении
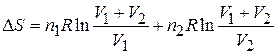 = – n1Rlnx1 – n1Rlnx2 =
= – n1Rlnx1 – n1Rlnx2 =
Задача № 5. Рассчитать стандартную энтропию 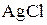 при
при 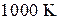 , если
, если 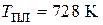 ,
, 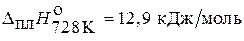 . Теплоемкости твердого и жидкого хлорида серебра постоянны и соответственно равны
. Теплоемкости твердого и жидкого хлорида серебра постоянны и соответственно равны 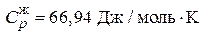 и
и 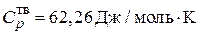 .
.
Решение.
1. Формула для расчета энтропии жидкого 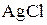 при
при 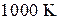 имеет следующий вид
имеет следующий вид
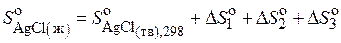 ,
,
где
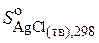 – энтропия твердого
– энтропия твердого 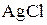 при
при 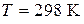
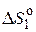 – изменение энтропии при нагревании
– изменение энтропии при нагревании 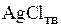 от
от 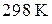 до
до 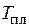 ,
,
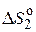 – изменение энтропии фазового перехода,
– изменение энтропии фазового перехода,
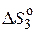 – изменение энтропии при нагревании
– изменение энтропии при нагревании 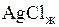 от
от 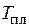 до
до 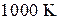 .
.
Находим в справочнике значение 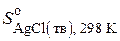
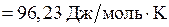 .
.
2. Рассчитываем 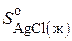 .
.
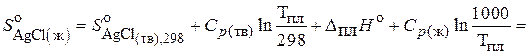

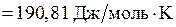
Задача № 6. Рассчитать абсолютную энтропию 2 моль 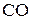 при
при 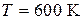 и
и 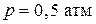 , считая
, считая 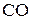 идеальным газом.
идеальным газом.
Решение.
1. Запишем формулу для вычисления энтропии газообразного 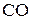 , как идеального газа, при
, как идеального газа, при 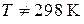 и
и 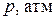 . Принимаем, что
. Принимаем, что 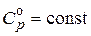 и равно
и равно 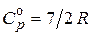 .
.
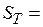
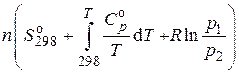
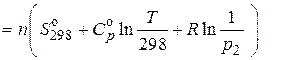
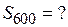
 .
.
Задача № 7. Пользуясь справочными данными, рассчитайте 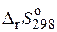 и
и 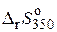 , для реакции:
, для реакции: 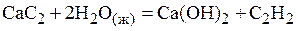 при
при 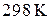 . Теплоемкости веществ, участников химической реакции, принять постоянными и равными средним значениям в интервале температур
. Теплоемкости веществ, участников химической реакции, принять постоянными и равными средним значениям в интервале температур 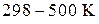 . Сделайте вывод о направлении протекания реакции в заданных условиях.
. Сделайте вывод о направлении протекания реакции в заданных условиях.
Решение.
1. Расчет 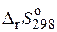 .
.
Расчет изменения энтропии в стандартных условиях при 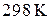 произведем на основании справочных данных о величинах
произведем на основании справочных данных о величинах 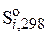 .
.
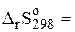
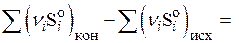
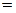
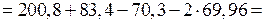
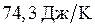 .
.
2. Расчет 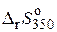 .
.
Для вычисления 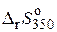 необходимо учесть зависимость
необходимо учесть зависимость 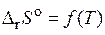 :
:
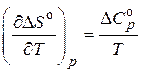
Интегрирование уравнения при 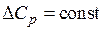 дает
дает
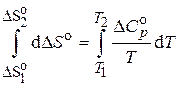
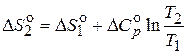
Или 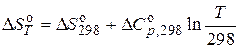
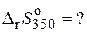
3. Вывод о направлении реакции?
Задача № 8. Рассчитайте стандартную энтропию 1 кг воды при: а) 10оС, б) 200оС. Теплоемкость жидкой и воды принять равной 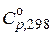 , для газообразной воды учесть зависимость
, для газообразной воды учесть зависимость 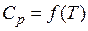 .
.
Решение.
1. 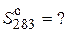
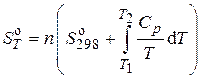
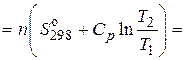
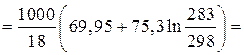
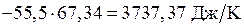 .
.
2. 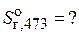
а) 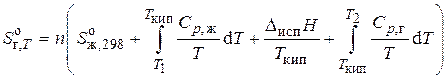 =
=
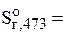
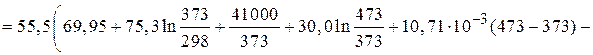
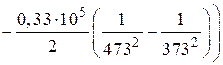 =
= 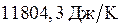
б) 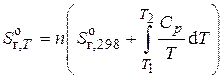
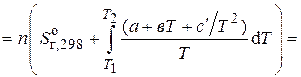
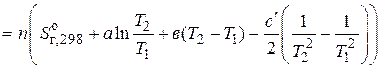
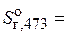 11356, 5 Дж/K
11356, 5 Дж/K
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|