Хелпикс

Главная

Контакты

Случайная статья



Контрольная работа по теме « Первообразная.Интеграл.» І вариант



Контрольная работа по теме « Первообразная. Интеграл. »   І вариант

1 Найдите первообразные данных функций:

      а) 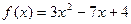                   б)

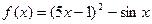
2 Вычислите интеграл:

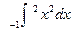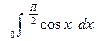     а)        б)           в)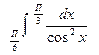

3 Решите неравенство: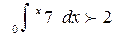

4 Найдите площадь фигуры, ограниченной линиями:

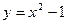    ; у=0; х=1; х=2.

5 Найдите площадь фигуры, ограниченной данной параболой и осью абсцисс:    

  

 

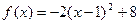
Контрольная работа по теме « Первообразная. Интеграл. »  ІІ вариант

1 Найдите первообразные данных функций:

    а)                      б)                                                                                                   

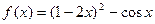
2 Вычислите интеграл:

                                                       

   а) 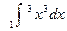             б)         в)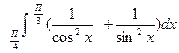

3 Решите неравенство:

 

4 Найдите площадь фигуры, ограниченной линиями:

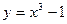   ; у=0; х=1; х=2.

5 Найдите площадь фигуры, ограниченной данной параболой и осью абсцисс:                         

 

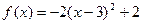
Контрольная работа по теме « Первообразная. Интеграл. »  ІIІ вариант

№1. Для функции f(x) = 2x2+x найдите первообразную, график которой проходит через точку А(1; 1)

№2. Вычислите интеграл:

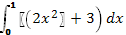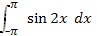а)     б)     в)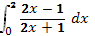

№3. Найдите площадь фигуры, ограниченной линиями:

а) параболой у=(х-1)2, прямой у=х+1 и осьюОх.

б) y=-x2+4, x=-1, x=1, y=0.

 

Контрольная работа по теме « Первообразная. Интеграл. »   ІV вариант

1. Для функции f(x) = 3x2-5 найдите первообразную, график которой проходит через точку А(-1; 3)

№2. Вычислите интеграл:

а) 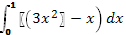   б)    в)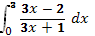

№3. Найдите площадь фигуры, ограниченной линиями:

а) параболой у=(2-х)2, прямой у=2х+4и осьюОх.

б) прямой у =3 – 2х и графиком функции у =х2 +3х – 3.

 

 

Контрольная работа по теме « Первообразная. Интеграл. »

V вариант

1. Найдите первообразную F функции f (x) = 2 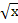, график которой проходит через точку А(0; ).

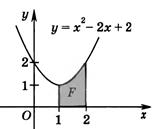
2. Вычислите площадь фигуры, изображенной на рисунке.

  1. Вычислить интеграл: а) 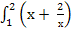dx; б)  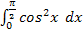    в)

4. Найдите площадь фигуры, ограниченной прямой у =1 –2х и графиком функции у =х2 – 5х – 3.

Вариант VI

1. Найдите первообразную F функции f(x)= - 3 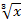, график которой проходит через точку А(0; ).

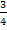2. Вычислите площадь фигуры, изображенной на рисунке.

  1. Вычислить интеграл: а) 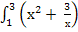dx; б) . в)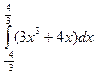

4. Вычислите площадь криволинейной трапеции, ограниченной линиями y=-x2+9, x=-1, x=1, y=0.

 



  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.