Контакты

Случайная статья

36.Інтегрування виразів, що що містять триногометричні функції.

⇐ ПредыдущаяСтр 2 из 2

36. Інтегрування виразів, що що містять триногометричні функції.

1*. Інтеграли вигляду .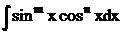

а) Якщо хоча б один з показників 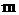або 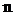- попарне додатне число, то інтегрування ведемо так:

нехай 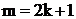, 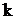є 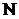. Від непарного степеня синуса відокремлюємо його першу степінь- вона потрібна для утворення диференціала косинуса; ту додатню степінь, котра залишилась, перетворюємо у косинус того ж самого аргументу за формулою: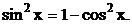

Далі робимо підстановку: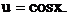

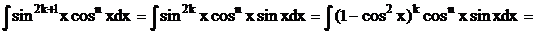
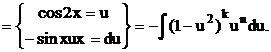
Далі за формулами скороченого множення розкриваємо дужки і отримуємо додатки степеневого вигляду.

Приклад.

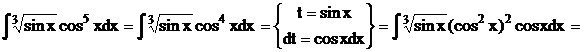
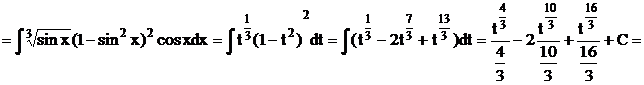
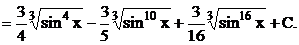
б) Якщо обидва показники 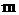і 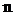- парні додатні числа, то інтеграл можна знайти, якщо поширити степінь підінтегральних виразів за допомогою формул:

; ;

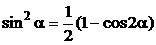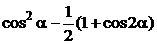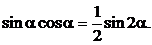
Приклад.

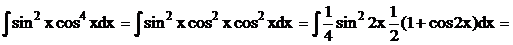
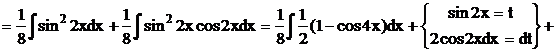
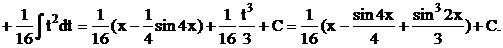
2*. Інтеграли вигляду ,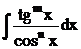

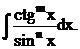
Якщо 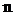- парне додатне число, то при будь-якому значенні 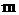, то використовуємо тригонометричні тотожності:

; ,

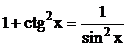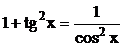а далі за допомогою підстановки 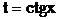або 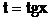одержимо інтеграли від степеневих функцій.

Приклад.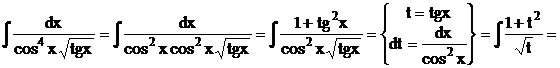

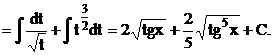
3*. Інтеграли вигляду

, ,

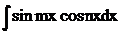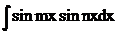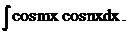
Ці інтеграли можна привести до табличних за допомогою формул:

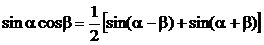
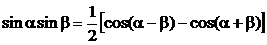
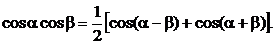
Приклад.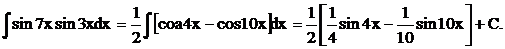

⇐ Предыдущая 12

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.