Восьмое ноября. Классная работа. 1) произведение двух натуральных чисел всегда является натуральным числом;. 2) частное двух натуральных чисел не всегда можно выразить натуральным числом;

Восьмое ноября

Классная работа

Тема: Деление нацело.

Число, которое делят, называется делимым , а то, на которое делят, — делителем . Результат действия деления называется частным.

Умножение и деление — взаимно обратные действия. Именно поэтому умножение проверяют делением, а деление — умножением.

Пусть а и b – натуральные числа и .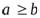

Определение. а делитсяна b нацело, если существует натуральное число с, при умножении которого на b получается а. а: b = с, т. к. а = b × с.

? Всегда ли одно натуральное число можно разделить на другое нацело? Не всегда. Например, частное 5: 3 невозможно выразить натуральным числом.

Любое натуральное число а делится на 1 и само на себя: а: 1 = а, а: а = 1 При делении нуля на любое число получается нуль: 0: а = 0, т. к. а × 0 = 0; Делить на нуль нельзя: а: 0 – нельзя.

Обратите внимание:

1) произведение двух натуральных чисел всегда является натуральным числом;

2) частное двух натуральных чисел не всегда можно выразить натуральным числом;

Свойство частного: Делимое и делитель можно умножить или разделить нацело на одно и то же натуральное число – частное от этого не изменится.

Пример 1. Использование свойства частного: 48: 8.

1) 48: 8 = 6;

2) (48 × 2): (8 × 2) = 96: 16 = 6;

3) (48: 4): (8: 4) = 12: 2 = 6.

Пример 2. Вычислите, используя свойство частного:

1) 3 600: 400 = (3 600: 100): (400: 100) = 36: 4 = 9;

2) 2 500: 50 = (2 500: 10): (50: 10) = 250: 5 = 50.

Обратите внимание: с помощью действия деления:

1. по известному произведению и одному из множителей находят второй множитель;

2. данное число уменьшают в указанное количество раз;

3. выясняют, во сколько раз одно число больше второго или меньше его.

Домашнее задание. § 1. 12 (выучить теорию), сделать краткий конспект.

Выполнить: на оценку 3-4: № 180(2ст. ), 184(2ст. ), 185(2ст. ).

Выполнить: на оценку 4-5: № 180(2ст. ), 185(2ст. ), 186(1-2 ст), 187 (3ст).