Лабораторная работа № 3. Разработка эффективных алгоритмов

Лабораторная работа № 3

Разработка эффективных алгоритмов

Разработайте алгоритмы решения задач с заданными параметрами эффективности.

1. Найти минимум и максимум двух натуральных чисел без использования операции сравнения c временной сложностью t = O(4) и емкостной сложностью e = O(4). Например, если a = 4, b = 5, то в результате работы алгоритма должно быть max = 5, min = 4.

2. Даны две числовые переменные a и b. Необходимо поменять местами их значения, без использования других переменных и операции сравнения, c временной сложностью t = O(5) и емкостной сложностью e = O(2). Например, если a = 4, b = 5, то в результате работы алгоритма должно быть a = 5, b = 4.

3. Для вводимой последовательности из n (5 £ n £ 50) чисел разработайте алгоритм вычисления суммы положительных чисел и суммы отрицательных чисел с временной сложностью t = O(n) и емкостной сложностью e = O(5).

4. Для вводимого натурального числа n (n < 2⁶⁴) разработайте алгоритм вычисления суммы и произведения его десятичных разрядов с временной сложностью t = O(k), где k – количество десятичных разрядов, и емкостной сложностью e = O(4).

5. Разработайте алгоритм преобразования натурального числа n из i позиционной системы счисления в j позиционную систему счисления с промежуточным преобразованием числа в десятичную систему счисления.

6. Разработайте алгоритм вычисления суммы членов натурального ряда в интервале от k₁ до k₂ c временной сложностью t = O(3) и емкостной сложностью e = O(3).

7. Разработайте алгоритм, определяющий, является ли автобусный билет счастливым, т. е. равны ли суммы старших и младших трех цифр шестизначного числа, c временной сложностью t = O(5) и емкостной сложностью e = O(3).

8. Разработайте алгоритм решения квадратного уравнения ax² + bx + c = 0, используя наиболее эффективные способы вычисления корней в частных случаях (учитываемые случаи: общий случай, a = 0, a = 1, b – четное, с = 0). Определите временную и емкостную сложности для всех случаев решения уравнения. Примечание: алгоритм должен включать несколько алгоритмических модулей.

9. Разработайте алгоритм вычисления функции v = f(x, y, z):

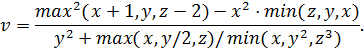
Примечание: для вычисления значений минимума и максимума должны использоваться отдельные алгоритмические модули.