Коды Хэмминга.

Линейные коды, обладающие параметрами

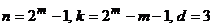, (6. 9)

называются кодами Хэмминга. Они исправляют любую однократную ошибку и не исправляют ни одной ошибки большей кратности.

Указанная связь между n, k и корректирующей способностью объясняется тем, что в этом случае число ненулевых синдромов 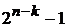равно числу однократных ошибок n.

При действии однократной ошибки, например 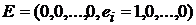синдром 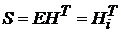равен транспонированному столбцу проверочной матрицы. Чтобы между синдромом и однократной ошибкой существовало взаимнооднозначное соответствие, столбцы проверочной матрицы кода Хэмминга должны быть различными и ненулевыми (нулевой синдром означает отсутствие ошибок). Перестановка столбцов матрицы приводит к эквивалентному коду Хэмминга.

Расширенный код Хэмминга.

Любой линейный 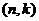код может быть расширен до кода с параметрами 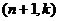путем добавления общей проверки на четность – еще одного проверочного символа, равного сумме по модулю 2 всех символов кодового слова. Пусть – произвольное кодовое слово исходного 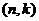линейного кода. Тогда соответствующее ему слово расширенного кода 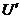может быть построено по правилу 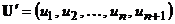, где – бит четности. Очевидно, что для любого кодового слова расширенного кода выполняется со-

отношение

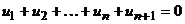и, следовательно, его вес будет четным. Тогда при нечетном кодовом расстоянии 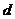исходного кода 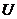минимальное расстояние расширенного 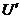увеличится на единицу, став 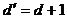. Таким образом, любой линейный 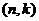код с нечетным 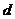, исправляющий 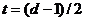ошибок, может быть трансформирован в расширенный 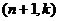код, исправляющий ошибки кратности 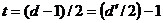и обнаруживающий ошибки кратности .

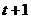При минимальном весе исходного кода Хэмминга, равном трем, после расширения получаем 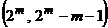код с расстоянием, равном 4, т. е. код, исправляющий любую однократную и обнаруживающий любую двукратную ошибки.

Ряд расширенных кодов Хэмминга содержит коды (4, 1), (8, 4), (16, 11), (32, 26), (64, 57) и т. д. Отметим, что код (4, 1) является кодом с повторением.