Хелпикс

Главная

Контакты

Случайная статья



10 ноября. Классная работа.



10 ноября

Классная работа.

Тема: Разложение квадратного трехчлена на множители.

При решении уравнений, действий с алгебраическими дробями бывает необходимо разложить квадратный трехчлен на линейные множители. Для этого необходимо учитывать следующую теорему.

Теорема. Если х1 и х2 корни квадратного трехчлена ах2 + вх + с,

то        ax2 + bx + c = a(x – x1)(x – x2).

Чтобы разложить квадратный трехчлен на линейные множители, нужно проанализировать наличие корней у данного трехчлена.

Пример—1       Разложим квадратный трехчлен на множители.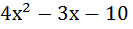

Решим уравнение 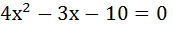, найдем корни квадратного трехчлена.

По теореме о разложении квадратного трехчлена имеем:

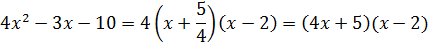
Пример —2      Разложим квадратный трехчлен на множители

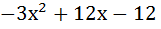
Решим уравнение 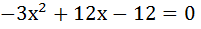, найдем корни квадратного трехчлена.

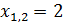
По теореме о разложении квадратного трехчлена имеем:

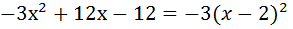
Пример —3      Сократить дробь: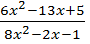  

Разложим квадратные трехчлены числителя и знаменателя на линейные множители:

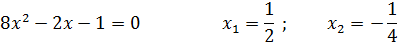
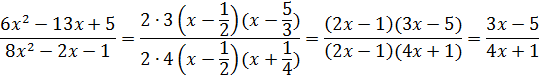
Выполнить самостоятельно:

1. Разложите на множители квадратный трёхчлен:

 

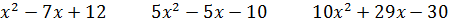
2. Сократите дробь        

Домашнее задание:     §2, п. 4 (стр. 27–29)          упр. № 76(а, б, в), 84
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.