В ориентированном, неориентированном или смешанном графе(т. е. таком, где часть ребер (дорог) имеет одностороннее движение)найти кратчайший путь между двумя заданными вершинами.

Алгоритм использует три массива, каждый длиной n, где n = числу вершин графа.

I массив a содержит метки с двумя значениями:

0 - вершина ещё не рассмотрена и 1 - вершина уже рассмотрена;

II массив b содержит расстояния – текущие кратчайшие расстояния от v_i до соответствующей вершины;

III массив c содержит номера вершин – k-й элемент c_k есть номер предпоследней вершины на текущем кратчайшем пути из v_i в v_k. Матрица расстояний D=|| d_i _k || задаёт длины ребер d_i _k; если такого ребра нет, то d_i _k присваивается большое число 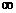, равное «машинной бесконечности».

Алгоритм Дейкстры

1 (инициализация). В цикле от 1 до n:

заполнить нулями массив а;

заполнить числом i массив с;

перенести i-тую строку матрицы D в массив b;

a[i]: =1; c[i]: =0; { i-номер стартовой вершины}

2. (общий шаг)

2. 1. Найти минимум среди неотмеченных вершин, т. е. тех, для которых a[k]=0;

т. е. j = min {b[k]}; a[j]: =1;

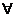k: a[k]=0

2. 2. если b [k]> b[j]+d[j, k] то b[k]: =b[ j] +d[j, k]; c[k]: =j

Условие означает, что путь v_i.. v_k длиннее, чем путь v_i.. v_j, v_k. Если все a[k] отмечены, то длина пути v_i.. v_k равна b[k]. Теперь надо перечислить вершины, входящие в кратчайший путь

3. (выдача ответа). Путь v_i.. v_k выдаётся в обратном порядке следующей процедурой:

3. 1. z: =c[k];

3. 2. Вывести z;

3. 3. z: =c[z]; Если z = 0, то конец, иначе перейти к 3. 2.

Для выполнения алгоритма нужно n раз просмотреть массив b из n элементов, т. е. алгоритм Дейкстры имеет квадратичную сложность. Проиллюстрируем работу алгоритма Дейкстры численным примером (для большей сложности, считаем, что некоторые города (вершины) i, j не соединены между собой, т. е. D[i, j] =∞ ).