3 ноября. Классная работа.

3 ноября

Классная работа.

Тема: Квадратный трехчлен и его корни.

Многочлен вида ax² + bx + cназывают квадратным трехчленом, где

a, bиc – некоторые числа, причем a≠ 0, а х – переменная.

Примеры квадратного трехчлена: 3х² – 2х – 5; х² + 7х – 8; — х² +2х + 5;
7х² – х; 4х².

Для того, чтобы найти корни квадратного трехчлена ax² + bx + c надо решить квадратно уравнение ax² + bx + c = 0.

Т. к. квадратный трехчлен имеет те же корни, что и квадратное уравнение, то он может иметь два корня, один корень или не иметь корней. Количество корней зависит от значения дискриминанта.

1. Если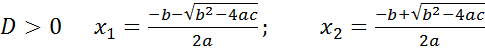

2. Если

3. Если , то квадратный корень из дискриминанта не существует, значит уравнение корней не имеет.

Пример: Найдем корни квадратного трехчлена 10х² – 5х – 5

Решим уравнение 10х² – 5х – 5 = 0

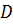= ( - 5)² + 4*10*5 = 225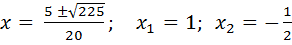

Значит квадратный трехчлен 10х² – 5х – 5 имеет два корня: 1 и - ½ .

При решении задач удобно бывает представить квадратный трехчлен в виде а(х – т)² + п, где «т и п» – некоторые числа. Такое преобразование называют выделением квадрата двучлена из квадратного трехчлена.

Пример: Выделим из трехчлена 2х²– 16х + 7 квадрат двучлена.

Вынесем за скобки множитель 2: 2(х²– 8х + ⁷/₂) —= 2(х²– 8х + ⁷/₂).

Преобразуем выражение в скобках. Для этого представим 8х в виде произведения 2*4*х, а затем прибавим и вычтем 4². Получим

2х²– 16х + 7 = 2(х²– 8х + ⁷/₂) —= 2(х²– 8х + 16 – 16 + ⁷/₂) = 2( (х – 4)² – 12, 5) =
= 2(х – 4)²– 25.

Выполнить самостоятельно:

№62 №64(а, б)

Домашнее задание: §2, п. 3 (стр. 22–24)
упр. №61, 65(а, б, г),