Задача 1.

1) Например, в теории межпланетных путешествий решается задача об определении массы топлива, необходимого для того, чтобы придать ракете нужную скорость v. Эта масса М зависит от массы m самой ракеты (без топлива) и от скорости v₀, с которой продукты горения вытекают из ракетного двигателя. Если не учитывать сопротивление воздуха и притяжение Земли, то масса топлива определяется формулой: М= m(e^v/v0-1) (формула К. Э. Циолковского). Например, для того чтобы ракета с массой 1. 5 т имела скорость 8000м/с, надо взять примерно 80 т топлива.

Радиоактивный распад вещества задаётся формулой m=m₀( 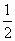) 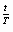, где m и m₀ масса радиоактивного вещества в момент времени t и в начальный момент времени t=0; T - период полураспада (промежуток времени, за который первоначальное количество вещества уменьшается вдвое). Когда радиоактивное вещество распадается, его количество уменьшается. Через некоторое время остаётся половина первоначального количества вещества. Чем больше период полураспада, тем медленнее распадается вещество.

Задача 1.

Период полураспада плутония Т=140 суткам. Какой станет масса m плутония через 10 лет, если его начальная масса m₀₌8г?

Решение.

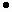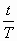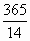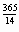
В данной задаче t=10 365 (считаем, что в году 365 дней), = . По формуле радиоактивного распада, с помощью микрокалькулятора находим m=8( ) 1, 1345 ^. 10^-7.

Ответ. Через 10 лет плутония останется 1 вари. 13 ^.10^-7 г.

Задача 2 / 2 ученика работают у доски/

При радиоактивном распаде количество некоторого вещества уменьшается вдвое за сутки. Сколько вещества останется от 250 г через: а) 1, 5 суток; б) 3, 5 суток?

Решение.

а) m₀₌250г

T=1 сут.

t=1, 5 сут.

m=m_{0 (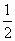} ₎^{1, 5}

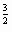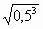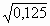
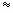
m=250 *0, 5 =250 =250 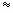88, 4(г).

б) m₀₌250г

T=1 сут.

t=3, 5 сут.

m=m_{0 (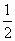} ₎^{3, 5}.

m=250 ∙ 0, 5^7/2=250 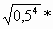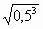= 250 ∙ 0, 25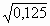 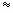22, 1(г).

Явление радиоактивного распада используется для определения возраста археологических находок, например, определён примерный возраст Земли (около 5, 5 млрд. лет).

3) Изменение атмосферного давления p в зависимости от высоты h над уровнем моря описывается формулой p=p₀a^k , где p₀ -атмосферное давление над уровнем моря, а – некоторая постоянная.

4) Все, наверное, замечали, что если снять кипящий чайник с огня, то сначала он быстро остывает, а потом остывание идёт гораздо медленнее. Дело в том, что скорость остывания пропорциональна разности между температурой чайника и температурой окружающей среды. Чем меньше становится эта разность, тем медленнее остывает чайник. Если сначала температура чайника равнялась Т₀, а температура воздуха Т_1, то через t сeкунд температура Т чайника выразится формулой: Т = (Т₁-Т₀) е^-кt+ Т_1, где к - число, зависящее от формы чайника, материала, из которого он сделан, и количества воды, которая в нём находится.

5) При падении тел в безвоздушном пространстве скорость их непрерывно возрастает. При падении тел в воздухе скорость падения тоже увеличивается, но не может превзойти определённой величины.

Рассмотрим задачу о падении парашютиста. Если считать, что сила сопротивления воздуха пропорциональна скорости падения парашютиста, т. е. что F=kv, то через t секунд скорость падения будет равна: v = mg/k(1-e^-kt/m),

где m -масса парашютиста. Через некоторый промежуток времени e^-kt/m станет очень маленьким числом, и падение станет почти равномерным. Коэффициент пропорциональности k зависит от размеров парашюта. Данная формула пригодна не только для изучения падения парашютиста, но и для изучения падения капли дождевой воды, пушинки и т. д.

Как видите, во всех приведенных выше исследованиях использовалась показательная функция {\displaystyle T} {\displaystyle g}

6) Пусть идеальный газ находится в поле консервативных сил в условиях теплового равновесия. При этом концентрация газа будет различной в точках с различной потенциальной энергией, что необходимо для соблюдения условий механического равновесия. Так, число молекул в единичном объеме n убывает с удалением от поверхности Земли, и давление, в силу соотношения P = nkT, падает.

Если известно число молекул в единичном объеме, то известно и давление, и наоборот. Давление и плотность пропорциональны друг другу, поскольку температура в нашем случае постоянна. Давление с уменьшением высоты должно возрастать, потому что нижнему слою приходится выдерживать вес всех расположенных сверху атомов.

Исходя из основного уравнения молекулярно-кинетической теории: P = nkT, заменим P и P₀ в барометрической формуле на n и n₀ и получим распределение Больцмана для молярной массы газа:

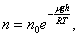
(2. 5. 1)

где n₀ и n - число молекул в единичном объёме на высоте h = 0 и h.

Так как 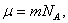а 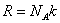, то (2. 5. 1) можно представить в виде

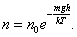
(2. 5. 2)

С уменьшением температуры число молекул на высотах, отличных от нуля, убывает. При T = 0 тепловое движение прекращается, все молекулы расположились бы на земной поверхности. При высоких температурах, наоборот, молекулы оказываются распределёнными по высоте почти равномерно, а плотность молекул медленно убывает с высотой. Так как mgh – это потенциальная энергия U, то на разных высотах U = mgh – различна. Следовательно, (2. 5. 2) характеризует распределение частиц по значениям потенциальной энергии:

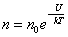(2. 5. 3)

– это закон распределения частиц по потенциальным энергиям – распределение Больцмана. Здесь n₀ – число молекул в единице объёма там, где U = 0.

На рисунке 2. 11 показана зависимость концентрации различных газов от высоты. Видно, что число более тяжелых молекул с высотой убывает быстрее, чем легких.

Ы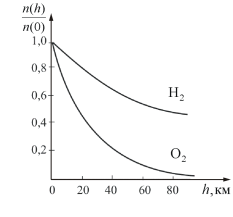
Рис. 2. 11

Из (2. 5. 3) можно получить, что отношение концентраций молекул в точках с U₁ и i> U₂ равно:

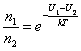(2. 5. 4)

Больцман доказал, что соотношение (2. 5. 3) справедливо не только в потенциальном поле сил гравитации, но и в любом потенциальном

{\displaystyle p=p_{0}\exp \left[-Mg{\frac {h-h_{0}}{RT}}\right], }