
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Группа11 Математика 03.11.2021год
Группа11 Математика 03. 11. 2021год
№32
Обобщение и систематизация ранее изученного школьного программного материала по геометрии.
Тема: Длина окружности и площадь круга.
Цель: повторить, ранее изученный, школьный программный материал по геометрии.
Формировать навыки самостоятельной работы студентов. Развитие логического мышления и пространственного воображения.
Учебник: Ш. А. Алимов Алгебра10-11
https: //foatk. ru/documents/book1. pdf
Рекомендации студентам, находящимся на дистанционном обучении.
Работать со скаченным файлом, т. к. файл, открытый в Интернете не всегда корректен. Определения и решенные упражнения, графики функций в домашних тетрадях должны быть записаны полностью.
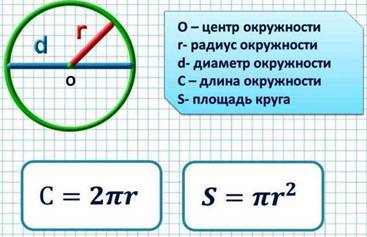
Задача 1. Найти площадь круга, если его радиус равен 2 см.
Так как площадь круга равна π умноженное на радиус в квадрате, то площадь круга с радиусом 2 см будет равна:
S ≈ 3, 14 · 22 = 3, 14 · 4 = 12, 56 (см в кв. )
Задача 2. Найти площадь круга, если его диаметр равен 7 см.
Сначала найдём радиус круга, разделив его диаметр на 2: 7: 2 = 3, 5 (см)
теперь вычислим площадь круга по формуле:
S = π r2 ≈ 3, 14 · 3, 52 = 3, 14 · 12, 25 = 38, 465 (см в кв. )
Задача 3.
Найти радиус круга, если его площадь равна 12, 56 м в кв.
Чтобы найти радиус круга по его площади, надо площадь круга разделить π, а затем из полученного результата извлечь квадратный корень:
r = √ S: π следовательно радиус будет равен: r ≈ √ 12, 56: 3, 14 = √ 4 = 2 (м)
Круг – это плоская фигура, которая представляет собой множество точек равноудаленных от центра. Все они находятся на одинаковом расстоянии и образуют собой окружность. Отрезок, который соединяет центр круга с точками его окружности, называется радиусом. В каждой окружности все радиусы равны между собой. Прямая, соединяющая две точки на окружности и проходящая через центр называется диаметром. Формула площади круга рассчитывается с помощью математической константы – числа π.. : Число π. представляет собой соотношение длины окружности к длине ее диаметра и является постоянной величиной. Значение π = 3, 1415926 получило применение после работ Л. Эйлера в 1737 г.

Домашнее задание: Отработать материал в домашних тетрадях, сфотографировать (скан. ) отправить на электронную почту преподавателя m. kayuck@yandex. ua
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|