
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Варіант №10. Роз’вязок
Варіант №10
Знайти цілочисельний розв’язок наступної задачі.
z= 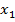 + 2
+ 2 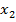
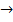 max
max
 2
2 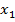 + k
+ k 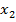
 7
7
(2+ k) 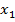 - k
- k 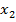
 9
9
x1. 2 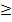 0, цілі числа, k=10
0, цілі числа, k=10
a) Знайти рішення методом Гоморі.
Роз’вязок
1. Знайти цілочисельний розв’язок наступної задачі.
Рішення:
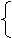 y1= -2
y1= -2 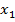 - 10
- 10 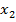 + 7
+ 7 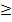 0
0
y2= -12 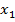 + 10
+ 10 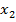 + 9
+ 9 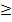 0
0
1. y1= -2 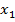 - 10
- 10 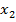 + 7
+ 7 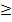 0
0
y1 = 0
-2 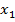 - 10
- 10 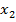 + 7 = 0
+ 7 = 0
x1 = 0, x2 = 7/10
x2 = 0, x1 = 7/2
y1(0) = 7 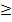 0
0
2. y2= -12 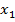 + 10
+ 10 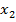 + 9
+ 9 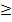 0
0
y2 = 0
-12 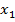 + 10
+ 10 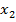 + 9
+ 9 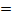 0
0
x1= 0, x2= -9/10
x2 =0, x1= 9/12
y2(0)= 9 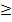 0
0
z= 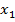 + 2
+ 2 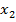 = 0
= 0
x1= 0, x2= 0
x1 =-2, x2= 1
a) Знайти рішення методом Гоморі.
|
| -x1 | -x2 | |
| y1= | |||
| y2= | -10 | ||
| z= | -1 | -2 |
|
| -x1 | -y1 | |
| x2= | 2/10 | 1/10 | 7/10 |
| y2= | |||
| z= | -1/10 | 2/10 | 14/10 |
|
| -x2 | -y1 | |
| x1= | 10/2 | 1/2 | 12/2 |
| y2= | -76/2 | -12/2 | -41/2 |
| z= | 1/2 | 1/2 | 12/2 |
т. М (12/2; 0) maxZ = z(M)= 12/2
Точка М нецілочисельна. Ми знайшли нецілочисельний оптимальний розвязок. Переходимо до другого етапу і знаходимо цілочисельний оптимальний розв’язок.
x1 = 12/2, складаємо додаткове обмеження.
S1 = β 11x2 + β 12y1 – β 1
S1= 1/2 x2 – 1/2 y1 – 1/2
|
| -x1 | -y1 | |
| x1= | 4, 5 | 0, 8 | 6, 5 |
| y2= | -44, 5 | -6, 5 | -30, 5 |
| s1= | 0, 8 | -0, 8 | -0, 8 |
| z= | 0, 8 | 0, 8 | 6, 5 |
|
| -x1 | -s1 | |
| x1= | |||
| y2= | -62 | -7 | -24 |
| y1= | -1 | -2 | |
| z= |
т. М (6; 0) maxZ= Z(M)=6
Точка М цілочисельна.
Висновок: На лабораторній роботі засвоєно метод відсікаючих площин (Гоморі) знаходження цілочисельного розв’язку.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|