Итерация 1.. Итерация 2.

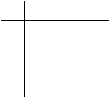
Пример. В данной сети (см. Рис. 1. 15) найти кратчайшую цепь между всеми парами узлов в сети.

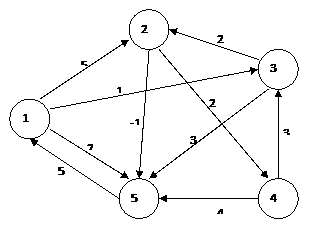
Рис. 1. 15

Решение: Составляются матрицы и .

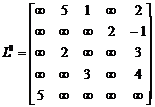
Итерация 1.

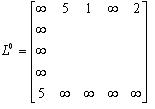
Узел p=1 определяется как базовый. Выделяем в матрице первую строку и первый столбец. Кроме того, строки 2, 3 и 4 в базовом столбце содержат элементы, равные , и, следовательно, эти строки не изменяться. Столбец 4 в базовой строке так же содержит элемент, равный , и он тоже не меняется. Поэтому для того, чтобы вычислить матрицу , следует исследовать лишь элементы матрицы , показанные ниже

Применяя к этим элементам алгоритм Флойда, получаем следующие матрицы:

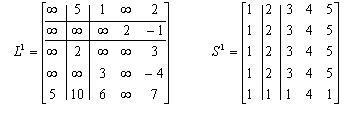
Итерация 2.

Определяем узел p=2 как базовый. Выделяем вторую строку и второй столбец в матрице и переписываем их без изменений. В ниже представленной матрице пропущены элементы, которые подлежат пересчету:

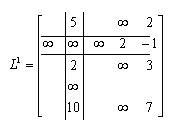
Используя алгоритм Флойда, получаем матрицы:

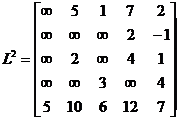
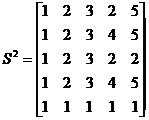
Далее аналогично действуя, получаем:

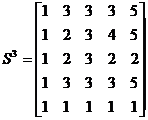
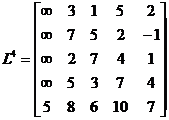
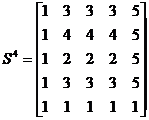
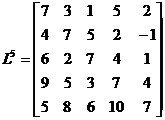
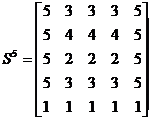
Длина кратчайшей цепи, например, из узла 5 в узел 4 равна 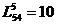. Для определения узлов соответствующей цепи, обратимся к матрице 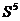. Нетрудно заметить, что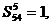 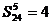. Следовательно, кратчайшая цепь из узла 5 в узел 4 определяется последовательностью узлов 5" 1" 3" 2" 4.

Замечание. Алгоритм Флойда может быть использован для нахождения в графе циклов отрицательной длины. Если на k-й итерации в матрице 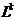на диагонали появилось отрицательное число 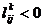, то это означает, что в графе существует цикл отрицательной длины. Найти цикл можно, используя справочную матрицу Sk.