Программа реализована на языке программирования Python .

Цифровая подпись Эль-Гамаля на эллиптическойкривой.

Часть 1. Теория:

Главным преимуществом схемы цифровой подписи Эль-Гамаля является возможность вырабатывать цифровые подписи для большого числа сообщений с использованием только одного секретного ключа. Чтобы злоумышленнику подделать подпись, ему нужно решить сложные математические задачи с нахождением логарифма в поле 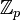. Следует сделать несколько комментариев:

· Случайное число 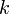должно сразу после вычисления подписи уничтожаться, так как если злоумышленник знает случайное число 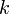и саму подпись, то он легко может найти секретный ключ по формуле: 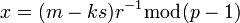и полностью подделать подпись.

Число 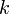должно быть случайным и не должно дублироваться для различных подписей, полученных при одинаковом значении секретного ключа.

· Использование свертки 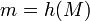объясняется тем, что это защищает подпись от перебора сообщений по известным злоумышленнику значениям подписи. Пример: если выбрать случайные числа 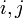, удовлетворяющие условиям 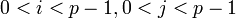, НОД(j, p-1)=1 и предположить что

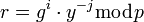
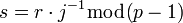
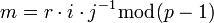
то легко удостовериться в том, что пара 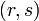является верной цифровой подписью для сообщения .

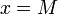· Цифровая подпись Эль-Гамаля стала примером построения других подписей, схожих по своим свойствам. В их основе лежит выполнение сравнения: 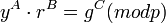, в котором тройка 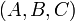принимает значения одной из перестановок ±r, ±s и ±m при каком-то выборе знаков. Например, исходная схема Эль-Гамаля получается при 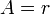, , 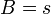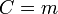. На таком принципе построения подписи сделаны стандарты цифровой подписи США и России. В американском стандарте DSS (DigitalSignatureStandard), используется значения 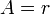, , 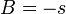, 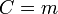а в Российском стандарте: , , .

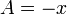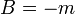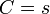· Еще одним из преимуществ является возможность уменьшения длины подписи с помощью замены пары чисел 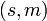на пару чисел 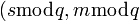), где 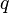является каким-то простым делителем числа 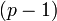. При этом сравнение для проверки подписи по модулю 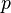нужно заменить на новое сравнение по модулю 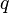: 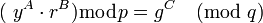. Так сделано в американском стандарте DSS (DigitalSignatureStandard).

Криптостойкость и особенности

В настоящее время криптосистемы с открытым ключом считаются наиболее перспективными. К ним относится и схема Эль-Гамаля, криптостойкость которой основана на вычислительной сложности проблемы дискретного логарифмирования, где по известным p, g и y требуется вычислить x, удовлетворяющий сравнению:

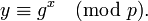
ГОСТ Р34. 10-1994, принятый в 1994 году в Российской Федерации, регламентировавший процедуры формирования и проверки электронной цифровой подписи, был основан на схеме Эль-Гамаля. С 2001 года используется новый ГОСТ Р 34. 10-2001, использующий арифметику эллиптических кривых, определенных над простыми полями Галуа. Существует большое количество алгоритмов, основанных на схеме Эль-Гамаля: это алгоритмы DSA, ECDSA, KCDSA, схема Шнорра.

Часть 2. Практика:

Программа реализована на языке программирования Python.

# -*- coding: utf-8 -*-

# создаёт кортеж (a, b) из чисел a и b

def zero(a, b):

if a is None: a=0

if b is None: b=0

return (a, b)

# колличество единиц в двоичном представление числа (хэш-функция для ФИАТА-ШАМИРА)

defoneOccur(n):

i = 0

for a in n:

while a< > 0:

if a%2==1:

i = i+1

a = a> > 1

return i

# нахождение обратного для n по модулю mod

defobr(n, mod):

for a in range(1, mod):

if n*a%mod==1:

return a

import random

p = 53

g = 7

x = 17

k, k_obr = None, None

whilek_obr is None:

k = random. randint(1, p-1)

k_obr = obr(k, p-1)

y = g**x%p

r = g**k%p

# подпись Эль-Гамаля

def EDS(mes):

h = oneOccur(mes)

s = (h-x*r)*k_obr%(p-1)

return (r, s)

# проверкаподписи

defcheckEDS(mes, sign):

h = oneOccur(mes)%p

return g**h%p, (y**sign[0])*(sign[0]**sign[1])%p

# многочлены для тестов

a = [1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 1]

b = [1, 0, 1]

#print devide(a[: ], b[: ]) # деление

#print GCD(a[: ], b[: ]) # НОД

#printkelli() # таблица келли над GF(32)

mes = [2, 4, 3, 76, 24, 4, 34] # сообщение

sign = EDS(mes) # подпись Эль-Гамаля

printsign

printcheckEDS(mes, sign) # проверкаподписи