
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тензор углового момента
ТЭН
Пусть Лагранжиан системы инвариантен относительно трансляций:
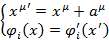
Или, как будет часто предполагаться, Лагранжиан не зависит от координат 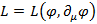 .
.
Как помним теорема Нерет говорит о сохранении следующих величинах:
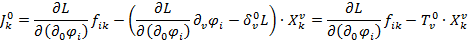
Преобразования координат приводящие к закону сохранения этих величин являются четырех парметрическими 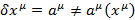 .
.
Значит в этом случае:
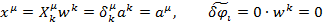
Подставляя, получаем:
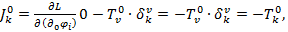 где
где 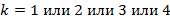
То есть сохраняющейся величиной является:

Где 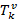 тензор энергии импульса:
тензор энергии импульса:
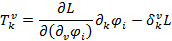
Четырех вектор с 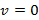 , то есть:
, то есть:

Называется вектором четырех импульса поля. Связано это с той аналогией которая возникает с механикой. А именно, компонента с 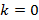 :
:
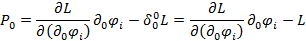
Напоминает выражение для гамильтониана в классической механике:
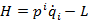
Поэтому ассоциируется с энергией. А величины:
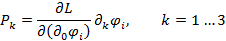
Определяют импульс поля. Таким образом, сохранение энергии – импульса имеет место для любой системы, лагранжиан которой не зависит явно от координат. Сделаем оба индекса контра вариантными или ковариантными:
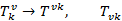
Есть некоторые физические причины, по которым предпочтительно использовать симметричный тензор энергии импульса:
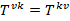
Примером такой причины можно взять из ибщей теории относительности. Уравнения Эйнштейна имеют вид:
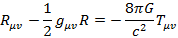
Где 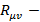 тензор Римана,
тензор Римана,  скалярная кривизна,
скалярная кривизна, 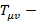 ТЭН. Левая часть этого равенства симметричная, значит должна быть симметричной и правая часть.
ТЭН. Левая часть этого равенства симметричная, значит должна быть симметричной и правая часть.
Однако ТЭН найденный по лагранжиану поля не всегда получается симметричным, но его можно сделать симметричным путем некоторого преобразования, а именно…
Как для 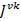 так и для
так и для 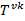 должно выполнятся уравнение непрерывности:
должно выполнятся уравнение непрерывности:
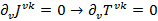
Которое можно написать так:
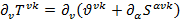
Где из тензора 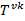 выделена симметричная часть
выделена симметричная часть 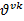 и величина
и величина 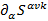 которая является антисимметричной по индексам
которая является антисимметричной по индексам 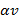 , а значит:
, а значит:
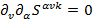
То есть:
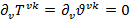
Где новая величина 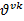 так же называется тензором энергии импульса, а именно симметризованным тензором энергии импульса, в отличии от величины
так же называется тензором энергии импульса, а именно симметризованным тензором энергии импульса, в отличии от величины 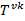 которая называется каноническим ТЭН.
которая называется каноническим ТЭН.
Примером подобного обстоятельства может служить ТЭН электромагнитного поля:
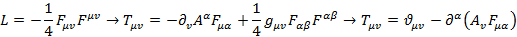
Тензор углового момента
Для введения тензора углового момента рассмотрим преобразования координат и полей связанные с преобразованиями Лоренца. Лоренц инвариантность является одним из требований предъявляемых к современным теориям. Бесконечно малые преобразования координат запишем в виде:
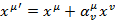
Величины 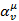 не являются произвольными. Именно, так как преобразования Лоренца сохраняют квадраты интервалов, то должно быть:
не являются произвольными. Именно, так как преобразования Лоренца сохраняют квадраты интервалов, то должно быть:
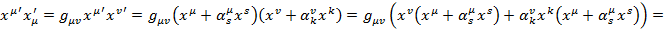
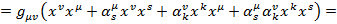
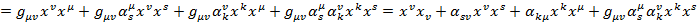
Величину второго порядка малости по 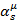 можно отбросить, тогда:
можно отбросить, тогда:
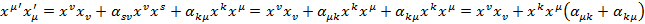
Для того что бы последнее выражение было равно 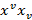 надо положить
надо положить 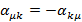 . В виду этого условия в матрице
. В виду этого условия в матрице 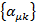 линейно независимыми являются всего 6 величин, индексы нумеруют плоскость в которой происходит вращение:
линейно независимыми являются всего 6 величин, индексы нумеруют плоскость в которой происходит вращение: 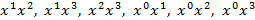 .
.
Далее, при преобразованиях Лоренца, поля 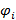 преобразуются по некоторому представлению группы Лоренца которое обозначим как
преобразуются по некоторому представлению группы Лоренца которое обозначим как 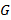 .
.
Около единичного элемента матричной группы 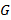 элемент группы
элемент группы 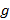 можно представить в виде:
можно представить в виде:
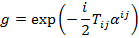
Коэффициент  введен для того, что бы два раза не учитывать одно и то же слагаемое
введен для того, что бы два раза не учитывать одно и то же слагаемое 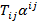 и
и 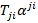 . Тут
. Тут
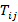 есть генераторы алгебры Ли группы
есть генераторы алгебры Ли группы 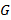 , и они тоже матрицы, то есть индексы
, и они тоже матрицы, то есть индексы 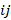 это не индексы элемента матрицы
это не индексы элемента матрицы 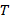 , а индексы генераторов. Генераторы должны удовлетворять тому же коммутационному соотношению что и генераторы группы Лоренца, хотя эта информация нам пока не пригодится. Далее, так как преобразования бесконечно малые, то элемент группы можно представить в виде:
, а индексы генераторов. Генераторы должны удовлетворять тому же коммутационному соотношению что и генераторы группы Лоренца, хотя эта информация нам пока не пригодится. Далее, так как преобразования бесконечно малые, то элемент группы можно представить в виде:
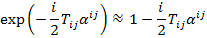
А поля 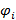 , если собрать их в один столбец:
, если собрать их в один столбец:
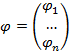
Преобразуются согласно равенству:
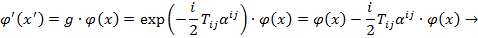
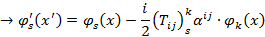
То есть преобразования полей и координат имеют вид:
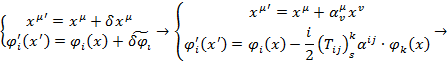
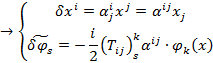
Как видно, в этом случае преобразования координат и полей являются шести параметрическими.
Далее, можно написать:
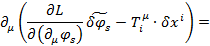
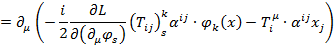
Далее напишем:
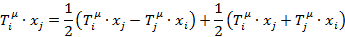
Тогда:
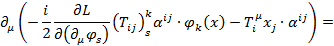
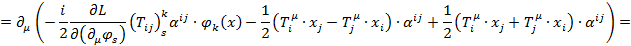
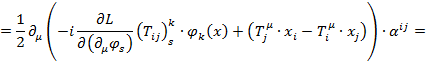
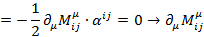
Где:
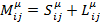
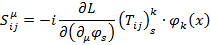
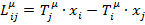
Таким образом мы пришли к уравнению непрерывности для тока 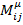 который называют тензором углового момента. При этом отдельно, величину
который называют тензором углового момента. При этом отдельно, величину  называют тензором орбитального момента, а величину
называют тензором орбитального момента, а величину 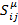 тензором спина.
тензором спина.
Сохраняющийся же угловой момент имеет вид:
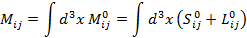
Можно рассматривать только пространственные компоненты выписанного выражения, то есть 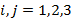 и построить компоненты трехмерного вектора по формуле:
и построить компоненты трехмерного вектора по формуле:

Построенный вектор называют вектором углового момента. Аналогично строятся вектора орбитального момента и спина:
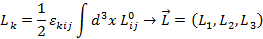
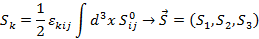
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|