Пример 3.. Пример 4.. 1. Логарифмпроизведения.. 2. Логарифмчастного.. 3. Логарифмстепени.. Пример 7.. Примеры и разбор решения заданий тренировочного модуля

Пример 3.

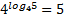(Читают: 4 в степени логарифм 5 по основанию 4 равен 5)

Пример 4.

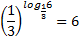(Читают: одна треть в степени логарифм 6 по основанию одна треть равен 6)

Решим несколько задач с использованием определения логарифма.

Задача 1. Вычислить .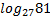

Решение. Пусть 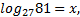тогда по определению логарифма 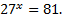Приведем левую и правую части к одному основанию. 27 = 3³, 81 = 3⁴, значит 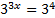. Отсюда следует, что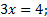

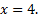
Задача 2. Вычислить .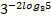

Решение. Для вычисления воспользуемся свойствами степеней: 1) 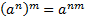, 2) 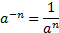и основным логарифмическим тождеством: .

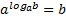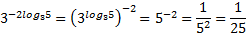Для решения более сложных задач потребуется знание свойств логарифмов. Рассмотримих.

1. Логарифмпроизведения.

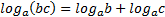
Логарифм произведения чисел 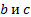по основанию 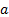равен сумме логарифма 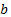по основанию 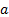и логарифма 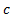пооснованию .

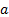Пример 5.

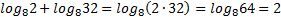
2. Логарифмчастного.

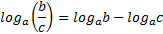
Логарифм частного чисел 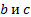по основанию 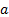равен разности логарифма 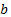по основанию 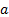и логарифма 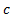пооснованию .

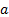Пример 6.

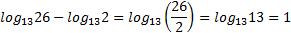
3. Логарифмстепени.

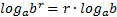
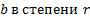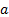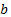Логарифм числа по основанию равен произведению показателя и логарифма по основанию .

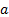Пример 7.

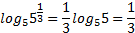
Важно! Свойства выполняются при ,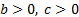

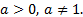
Примеры и разбор решения заданий тренировочного модуля

№ 1. Вычислите: .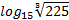

Решение:

Чтобы выполнить это задание нам понадобятся следующие определения и свойства:

;
.

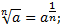
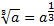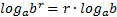Представим 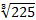в виде степени с рациональным показателем: 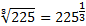. Далее воспользуемся свойством нахождения логарифма степени: 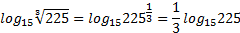. Вспоминаемтаблицуквадратов: 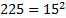, значит 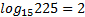, 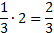. Ответ: .

⇐ Предыдущая 123 Следующая ⇒