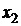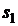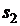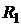Приклад 1

Розглянемо приклади використання двохетапного методу.

Приклад 1

Нехай маємо математичну модель:

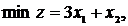
	(1)
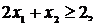
	(2)
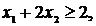
	(3)
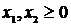
	(4)

Приведемо задачу до канонічної форми:

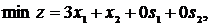
	(5)
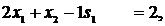
	(6)
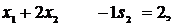
	(7)
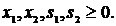
	(8)

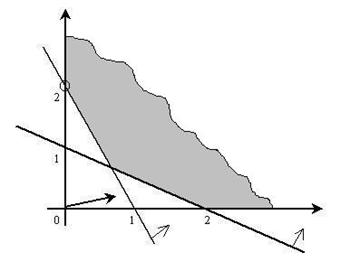
Рисунок 3

Етап I

1. Введемо штучні змінні в обмеження (2) і (3) (бо початково ці обмеження мали вигляд “³ ”). Позначимо штучні змінні 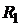та 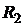відповідно. Тоді модель (5)–(8) прийме такий вигляд:

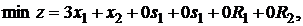
	(9)
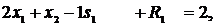
	(10)
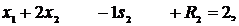
	(11)
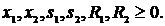
	(12)

2. На першому етапі двохетапного методу необхідно мінімізувати допоміжну ЦФ 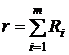. В нашому випадку: .

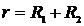Виразимо 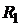та 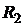із рівнянь (10), (11) відповідно:

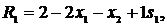
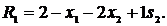
Підставимо ці вирази в цільову функцію :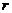

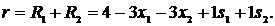
Перетворюємо її до наступного вигляду:

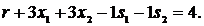
3. Будуємо початкову симплекс-таблицю двохетапного методу. Рядок 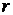заповнюємо відповідно до виразу, який було знайдено на попередньому кроці. ЦФ 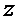(9) перетворюється до вигляду:

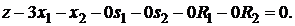
після чого заповнюємо 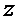–рядок таблиці.

Базисними змінними є змінні 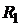та .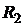

Базисні змінні					Розв’язок
(min)			–1	–1
	–3	–1
			–1			2/1=2
				–1		2/2=1 (min)

Тепер розв’яжемо задачу табличним симплекс–методом, приймаючи рядок 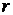– рядком цільової функції, а над рядком 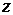будемо виконувати ті ж самі перетворення, що й над звичайними обмеженнями, що дозволить нам по закінченню етапу І отримати повну інформацію про початковий ДБР етапу ІІ. Згідно умови оптимальності для задачі на мінімум у базис вводиться змінна, котрій відповідає додатна відносна оцінка (додатний коефіцієнт 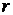–рядка). В нашому випадку в базис можна ввести як 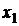так і 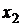. Зупинимось на змінній 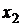. Згідно умови допустимості виводимо з базису змінну .

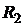Отримуємо таблицю:

Базисні змінні					Розв’язок
(min)	3/2	–1	1/2	–3/2
	–5/2		–1/2	½
	3/2	–1	1/2	–1/2		2/3 (min)
	1/2		–1/2	1/2

Оскільки не всі коефіцієнти цільової функції 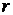не додатні, то продовжуємо ітерації симплекс–метода. Згідно умови оптимальності вводимо в базис змінну 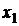та згідно умови допустимості виводимо з базису змінну 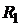. Отримуємо таблицю:

Базисні змінні					Розв’язок
(min)			–1	–1
	–5/3	1/3	5/3	–1/3	8/3
	–2/3	1/3	2/3	–1/3	2/3
	1/3	–2/3	–1/3	1/3	2/3

В останній таблиці виконується умова оптимальності для цільової функції 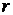, тобто ми отримали розв’язок, в якому ця функція досягає мінімуму. Оскільки оптимальне значення функції 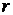дорівнює нулю, початкова задача має допустимий розв’язок – переходимо до етапу II.

12 Следующая ⇒