Действительные числа. Абсолютная величина действительного числа.

Все рациональные и иррациональные числа образуют множество действительных чисел.

Абсолютнойвеличиной (или модулем ) действительного числа х (обозначается |x|)называется неотрицательное действительное число, удовлетворяющее условиям: |x| = х, если x > 0 и |x| = - x, если х < 0.

Например: |2| = 2; |- 5| =5; |0| = 0. Из определения следует, что для любого х справедливо соотношение .

Рассмотрим некоторые свойства абсолютных величин.

1. Абсолютная величина алгебраической суммы нескольких действительных чисел не больше суммы абсолютных величин слагаемых: .

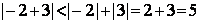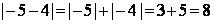Примеры: или ; или

2. Абсолютная величина разности не меньше разности абсолютных величин уменьшаемого и вычитаемого: .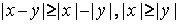

3. Абсолютная величина произведения равна произведению абсолютных величин сомножителей: .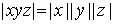

4. Абсолютная величина частного равна частному абсолютных величин делимого и делителя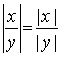

Последние два свойства непосредственно следуют из определения абсолютной величины.

Потребности практики, в частности необходимость использовать решения квадратного уравнения 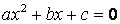с отрицательным дискриминантом (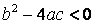), которое не имеет решений в области действительных чисел, привели к необходимости расширения понятия числа, отличного от действительного. Возникла необходимость в новых числах, отличных от действительных и включающих в себя множество действительных чисел.