
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема. Свойства добавление натуральных чисел
Цель: повторить и систематизировать знания учащихся о переставляющейся и соединительную свойства сложения; сформировать навыки применения свойств сложения при решении упражнений на добавление.
Тип урока: комбинированный.
Оборудование: схема «Свойства сложения».
Ход урока
I. Проверка домашнего задания
№ 197
| 1) | 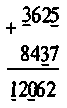
|
II. Актуализация опорных знаний
Устные упражнения
1. Найдите сумму слагаемых: 24 и 36; 18 и 22; 13 и 47; 51 и 49.
2. Плитка шоколада стоит 2 грн. 40 к., а пирожное - 70 к Сколько стоят: 1) плитка шоколада и пирожное; 2) плитка шоколада и два пирожных; 3) две плитки шоколада и пирожное?
3. Сумма двух чисел больше одного из них на 237. Чему равно второе число?
III. Повторение и систематизация знаний учащихся
Во время повторения материала удобно будет опираться на таблицу-схему (см. табл. ).
Свойства сложения
| 1. Переставная а + b = b+ a. | Пример: 64 + 23 = 23 + 64 |
| 2. Соединительная (a + b) + c = b + (a + c) = a + (b + c) | Пример: 1) (64 + 23) + 77 = 64 + (23 + 77) = 64 + 100 = 164. 2) 136 + (а + 214) =136 + (214 + а) = (136 + 214) + а = 350 + а. 3) 37 + 29 + 13 + 41 = (37 + 13) + (29 + 41) = -50 + 70 = 120 |
IV. Формирование навыков
Устные упражнения
1. Найти сумму наиболее удобным способом.
1) 26 + 19 + 34 + 51;
2) 32 + 29 + 28 + 41;
3) 630 + 40 + 160 + 70:
2. Увеличить сумму чисел 37 и 18 на 13.
Письменные упражнения
№183 (1, 3, 5, 7).
@ Следует еще раз обратить внимание на необходимость выбрать наиболее «удобный» порядок действий («удобство» обусловлена желанием получить «круглое» число).
№189 (1, 3, 5, 7).
@ Упростить выражение - то есть выполнить действия можно лишь добавив числовые слагаемые. Для этого и применяем переставной и соединительный законы сложения.
№ 193.
@ Решение примеров № 1, 2, 6, 7 можно сделать в виде упрощения выражений с применением переставного и связующего законов сложения.
[Пусть первый слагаемое а, а второй - b, их сумма а + b.
1) (а + 12) + b = (а + b) + 12 - сумма увеличится на 12;
2) (a + 23) + (b + 17) = (a + b) + 40 - сумма увеличится на 40 и др. ]
№ 199, 200.
@ Решение можно сопроводить рассказом про Карла Гаусса.
V. Домашнее задание
п. 7, №№ 18455 190; 191; 197 (2). Дополнительно № 201.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|