
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ПРАВОНАРУШЕНИЯ. (тысяч человек )
.
« Построение модели множественной линейной регрессии»
Исходные данные:
1. Сфера:
«Население» à «Правонарушения» (информация с сайта www. gks. ru)
2. Выбрано 3 показателя:
· Число лиц потерпевших от преступных посягательств,
· Зарегистрировано преступлений,
· Выявлено лиц, совершивших преступления;
3. Найдены данные по временным рядам выбранных показателей длиной 10 уровней: 2006, 2007, 2015 г.
|
ПРАВОНАРУШЕНИЯ (тысяч человек ) | |||||
| № показателя | Год | ||||
| Число лиц потерпевших от преступных посягательств (Y) | Зарегистрировано преступлений(X1) | Выявлено лиц, совершивших преступления (X2) | |||
| 3855, 4 | 1360, 9 | ||||
| 2675, 1 | 3582, 5 | 1317, 6 | |||
| 2303, 8 | 3209, 9 | 1256, 2 | |||
| 1953, 2 | 2994, 8 | 1219, 8 | |||
| 1785, 2 | 2628, 8 | 1111, 1 | |||
| 1656, 7 | 2404, 8 | 1041, 3 | |||
| 1639, 3 | 2302, 2 | 1010, 9 | |||
| 1566, 9 | 2206, 2 | 1012, 6 | |||
| 1595, 7 | 2190, 6 | ||||
| 1699, 1 | 2388, 5 | 1075, 3 | |||
Проведем обработку полученных данных.
Для этого выполним:
1. Вычислить элементы матрицы парных коэффициентов корреляции.
Рассчитаем сначала парные коэффициенты корреляции:
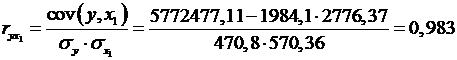
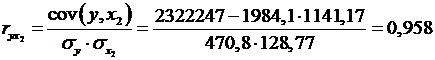
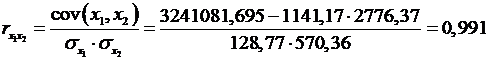
Анализ матрицы коэффициентов парной корреляции показывает, что зависимая переменная, т. е. число лиц потерпевших от преступных посягательств, имеет наиболее тесную связь с количеством зарегистрированных преступлений( 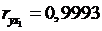 ) и с числом выявленных лиц, совершивших преступления (
) и с числом выявленных лиц, совершивших преступления ( 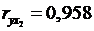 ). Зависимость числа лиц потерпевших от преступных посягательств со всеми включенными в модель факторами – прямая.
). Зависимость числа лиц потерпевших от преступных посягательств со всеми включенными в модель факторами – прямая.
2. Проверить факторы на наличие коллинеарности.
В случае построения многофакторной модели требуется проверить факторы на мультиколлинеарность. Коэффициент корреляции между факторами 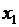 и
и 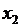 (равный 0, 991) больше 0, 7, т. е. мультиколлинеарность присутствует, и следовательно при построении многофакторной регрессии один из этих факторов следует удалить из рассмотрения.
(равный 0, 991) больше 0, 7, т. е. мультиколлинеарность присутствует, и следовательно при построении многофакторной регрессии один из этих факторов следует удалить из рассмотрения.
3. Составить уравнение регрессии в стандартизированном масштабе.
Коэффициенты 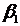 и
и 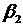 , стандартизованного уравнения регрессии
, стандартизованного уравнения регрессии
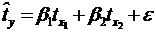 находятся по формуле:
находятся по формуле:

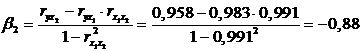
Т. е. уравнение будет выглядеть следующим образом:
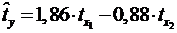 .
.
Так как стандартизованные коэффициенты регрессии можно сравнивать между собой, то можно сказать, что количество зарегистрированных преступленийоказывает большее влияние на число лиц потерпевших от преступных посягательств, чем число выявленных лиц, совершивших преступления.
4. Вычислить параметры уравнения чистой регрессии.
Находим по формулам коэффициенты чистой регрессии и
параметр 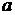 :
:
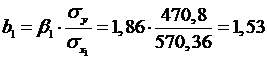
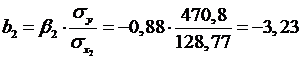
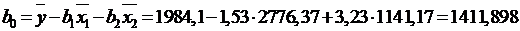
Таким образом, получили следующее уравнение множественной
регрессии:
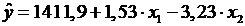
5. Вычислить индекс множественной линейной корреляции и проверить его значимость.
Коэффициент множественной корреляции определить через матрицы
парных коэффициентов корреляции:
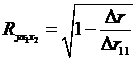 ,
,
где
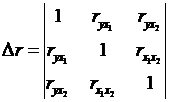
определитель матрицы парных коэффициентов корреляции;
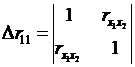
определитель матрицы межфакторной корреляции.
Находим:
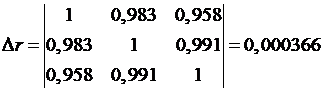
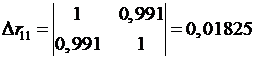
Коэффициент множественной корреляции:
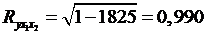
Аналогичный результат получим при использовании формул:
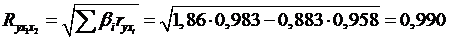
Коэффициент множественной корреляции указывает на весьма
сильную связь всего набора факторов с результатом.
Нескорректированный коэффициент множественной детерминации 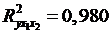 оценивает долю дисперсии результата за счет представленных в уравнении факторов в общей вариации результата. Здесь эта доля составляет 98% и указывает на весьма высокую степень обусловленности вариации результата вариацией факторов, иными словами - на весьма тесную связь факторов с результатом.
оценивает долю дисперсии результата за счет представленных в уравнении факторов в общей вариации результата. Здесь эта доля составляет 98% и указывает на весьма высокую степень обусловленности вариации результата вариацией факторов, иными словами - на весьма тесную связь факторов с результатом.
Скорректированный коэффициент множественной детерминации
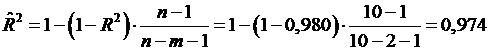
определяет тесноту связи с учетом степеней свободы общей и остаточной дисперсий. Он дает такую оценку тесноты связи, которая не зависит от числа факторов и поэтому может сравниваться по разным моделям с разным числом факторов. Оба коэффициента указывают на весьма высокую связь (более 97%) детерминированность результата  в модели факторами
в модели факторами  и
и 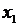 .
.
Оценку надежности уравнения регрессии в целом и показателя
тесноты связи 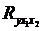 дает
дает 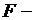 критерий Фишера:
критерий Фишера:
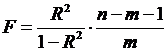
В нашем случае фактическое значение Т7-критерия Фишера:

Получили, что 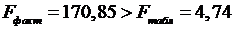 (при
(при 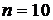 ), т. е. вероятность случайно получить такое значение
), т. е. вероятность случайно получить такое значение  критерия не превышает допустимый уровень значимости 5%. Следовательно, полученное значение не случайно, оно сформировалось под влиянием существенных факторов, т. е. подтверждается статистическая значимость всего уравнения и показателя тесноты связи
критерия не превышает допустимый уровень значимости 5%. Следовательно, полученное значение не случайно, оно сформировалось под влиянием существенных факторов, т. е. подтверждается статистическая значимость всего уравнения и показателя тесноты связи  .
.
6. Вычислить частные коэффициенты корреляции и проверить их значимость.
Частные коэффициенты корреляции характеризуют тесноту связи
между результатом и соответствующим фактором при элиминировании
(устранении влияния) других факторов, включенных в уравнение
регрессии.
При двух факторах частные коэффициенты корреляции
рассчитываются следующим образом:
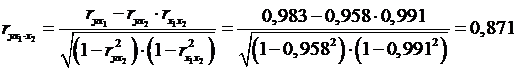
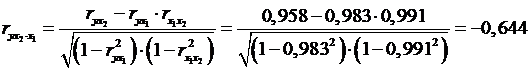
Если сравнить коэффициенты парной и частной корреляции, то
можно увидеть, что из-за высокой межфакторной зависимости
коэффициенты парной корреляции дают завышенные оценки тесноты
связи. Именно по этой причине рекомендуется при наличии сильной
коллинеарности (взаимосвязи) факторов исключать из исследования тот фактор, у которого теснота парной зависимости меньше, чем теснота
межфакторной связи.
| Парные коэффициенты корреляции | Частные коэффициенты корреляции |
| 0, 98 | > | 0, 871 | число лиц потерпевших от преступных посягательств и зарегистрировано преступлений |
| 0, 96 | > | – 0, 644 | число лиц потерпевших от преступных посягательств и выявлено лиц, совершивших преступления |
| 0, 99 | > | 0, 93 | зарегистрировано преступлений и выявлено лиц, совершивших преступления |
Таким образом,
4 между числом лиц потерпевших от преступных посягательств и зарегистрированными преступлениями связь 0, 98 и 0, 871 (прямая, положительная) – и по парному и по частному коэффициентам корреляции. Это говорит о том, что увеличение или уменьшение одного признака сопровождается аналогичным изменением другого признака;
- связь по парному коэффициенту 0, 98 – с учетом воздействия выявленных лиц, совершивших преступления
- связь по частному коэффициенту 0, 871 – без учета воздействия, но при фиксированном выявлено лиц, совершивших преступления
Значит, между данными показателями весьма высокая связь и по парному и по частному коэффициентам корреляции.
4между числом лиц потерпевших от преступных посягательств и выявленными лица, совершивших преступления связь 0, 96 (прямая, положительная) по парному и – 0, 644 (обратная, отрицательная) по частному коэффициентам корреляции. Это говорит о том, что увеличение или уменьшение одного признака сопровождается аналогичным изменением другого признака по парному коэффициенту корреляции и это означает, что увеличение или уменьшение одного показателя сопровождается противоположным по направлению изменением другого показателя –по частному коэффициентам корреляции;
- связь по парному коэффициенту 0, 96 – с учетом воздействия зарегистрированных преступлений
- связь по частному коэффициенту - 0, 644 – без учета воздействия, но при фиксированном значении зарегистрированных преступлений
Следовательно, между данными показателями прямая связь по парному коэффициентам корреляции и обратная связь по частному коэффициентам корреляции.
4 связь между зарегистрированными преступленийи выявленными лицами, совершившими преступления связь 0, 99 и 0, 93 (прямая, положительная) – и по парному и по частному коэффициентам корреляции. Это говорит о том, что увеличение или уменьшение одного признака сопровождается аналогичным изменением другого признака;
- связь по парному коэффициенту 0, 99 – с учетом воздействия числа лиц потерпевших от преступных посягательств
- связь по частному коэффициенту 0, 93 – без учета воздействия, но при фиксированном числе лиц потерпевших от преступных посягательств
Значит, между данными показателями весьма высокая связь и по парному и по частному коэффициентам корреляции.
4 в данной задаче парные коэффициенты корреляции незначительно отличны от частных коэффициентов, отсюда следует, что фиксированные величины ослабляют взаимосвязь между изучаемыми переменными. А так как частные коэффициенты меньше парных, то можно сделать вывод, что с учетом влияния других факторов связь больше, чем без учета взаимодействия их с другими показателями.
Значимость частных и парных коэффициентов корреляции, т. е. гипотеза H0: ρ = 0, проверяется по t-критерию Стьюдента. Наблюдаемое значение критерия находится по формуле:

где r – соответственно оценка частного или парного коэффициента корреляции; l – порядок частного коэффициента корреляции, т. е. число фиксируемых факторов.
α = 0. 05, ν = n − l − 2 = 10 – 1 – 2 = 7 tкр = 2, 365
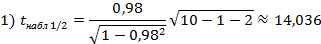
Т. к. |tнабл 1/2| > tкр (|14, 036| > 2, 365), то гипотеза Н0: ρ =0 отвергается, т. е. частный коэффициент корреляции не равен нулю (ρ 1 ≠ 0) – значимый частный коэффициент корреляции
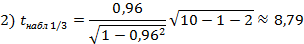
Т. к. |tнабл 1/3| > tкр (|8, 79| > 2, 365), то гипотеза Н0: ρ =0 отвергается, т. е. частный коэффициент корреляции не равен нулю (ρ 1 ≠ 0) – значимый частный коэффициент корреляции
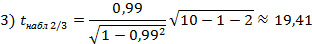
Т. к. |tнабл 2/3| > tкр (|19, 41| > 2, 365), значит, гипотеза H0: ρ =0 отвергается, т. е. частный коэффициент корреляции не равен нулю – значимый частный коэффициент корреляции.
7. Выполнить отсев факторов (если это необходимо).
(a) Если производится отсев факторов, то повторяются действия 1, 3-7
Для этого выполним:
Рассчитаем сначала парные коэффициенты корреляции:
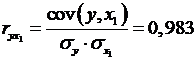
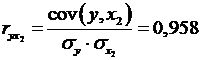
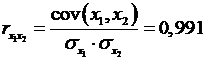
Анализ матрицы коэффициентов парной корреляции показывает, что зависимая переменная, т. е. число лиц потерпевших от преступных посягательств, имеет наиболее тесную связь с количеством зарегистрированных преступлений( 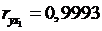 ) и с числом выявленных лиц, совершивших преступления (
) и с числом выявленных лиц, совершивших преступления ( 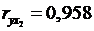 ). Зависимость числа лиц потерпевших от преступных посягательств со всеми включенными в модель факторами – прямая.
). Зависимость числа лиц потерпевших от преступных посягательств со всеми включенными в модель факторами – прямая.
В модели множественной регрессии с факторами 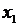 и
и 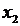 с
с 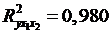 присутствует мультиколлинеарность и следовательно при построении регрессии один из этих факторов следует удалить из рассмотрения. Удаляем фактор
присутствует мультиколлинеарность и следовательно при построении регрессии один из этих факторов следует удалить из рассмотрения. Удаляем фактор 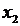 как менее информативный. Если исключить фактор
как менее информативный. Если исключить фактор 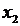 , то можно ограничиться уравнением парной регрессии:
, то можно ограничиться уравнением парной регрессии:
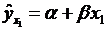 .
.
Найдем его параметры:
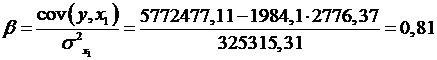

Таким образом:
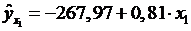 ,
, 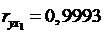
Коэффициент множественной детерминации 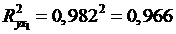 оценивает долю дисперсии результата за счет представленных в уравнении факторов в общей вариации результата. Здесь эта доля составляет 96, 6% и указывает на весьма высокую степень обусловленности вариации результата вариацией фактора, иными словами - на весьма тесную связь фактора с результатом.
оценивает долю дисперсии результата за счет представленных в уравнении факторов в общей вариации результата. Здесь эта доля составляет 96, 6% и указывает на весьма высокую степень обусловленности вариации результата вариацией фактора, иными словами - на весьма тесную связь фактора с результатом.
Оценку надежности уравнения регрессии в целом и показателя
тесноты связи 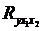 дает
дает 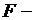 критерий Фишера:
критерий Фишера:
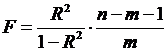
В нашем случае фактическое значение Т7-критерия Фишера:
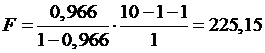
Получили, что 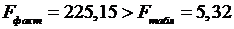 (при
(при 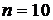 ), т. е. вероятность случайно получить такое значение
), т. е. вероятность случайно получить такое значение 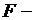 критерия не превышает допустимый уровень значимости 5%. Следовательно, полученное значение не случайно, оно сформировалось под влиянием существенных факторов, т. е. подтверждается статистическая значимость всего уравнения и показателя тесноты связи
критерия не превышает допустимый уровень значимости 5%. Следовательно, полученное значение не случайно, оно сформировалось под влиянием существенных факторов, т. е. подтверждается статистическая значимость всего уравнения и показателя тесноты связи 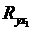 .
.
(b) Если отсев факторов не производится, переходим к пункту 8.
8. Проверить значимость окончательного уравнения регрессии.
Средняя ошибка аппроксимации по формуле:

Найдем величину средней ошибки аппроксимации 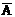 :
:
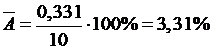 .
.
В среднем, расчетные значения отклоняются от фактических на 3, 31% поскольку ошибка меньше 10%, то данное уравнение можно использовать в качестве регрессии.
Работу нужно выполнить в двух вариантах.
Вариант 1: работа выполняется вручную, все необходимые расчеты проводятся с помощью калькулятора или ППП Excel (но в функции калькулятора).
Вариант 2: Решение задачи с помощью ППП Excel с использованием статистических функций. В заключении сравнение результатов, полученных в двух вариантах расчетов.
Вычислить элементы матрицы парных коэффициентов корреляции.
Для построения корреляционного анализа воспользуемся пакетом прикладных программ Microsoft Excel, функцией «Анализ данных».
Выполняем следующие действия:
1. Данные для корреляционного анализа должны располагаться в смежных диапазонах ячеек.
2. Выбрать команду «Сервис» → «Анализ данных».
3. В диалоговом окне «Анализ данных» выбрать инструмент «Корреляция», а затем щелкнуть кнопку «ОК».
4. В диалоговом окне «Корреляция» в поле «Входной интервал» необходимо ввести диапазон ячеек, содержащих исходные данные. Если введены и заголовки столбцов, то установить флажок «Метки в первой строке».
5. Выбрать параметры вывода. В данном случае «Новый рабочий лист».
6. «ОК»
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|