
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Замечание. Данноеутверждениеназывают пространственнойтеоремойПифагора.
ранеемы с вами уже познакомились с параллелепипедом. Напомню, что параллелепипед – эточетырехугольная призма, основаниямикоторойявляютсяпараллелограммы.
Выяснили, чтоесли все боковые ребра параллелепипедаперпендикулярны к плоскостям его оснований, т. е. боковые грани – прямоугольники, то такойпараллелепипедназывается прямым. Еслипараллелепипед не являетсяпрямым, т. е. если все его боковые ребра не перпендикулярны к плоскостям оснований, то он называется наклонным. Если же и основаниями прямого параллелепипедаслужатпрямоугольники, то такойпараллелепипедназывается прямоугольным.
А также узнали, что параллелепипедобладаетследующимисвойствами:
1) противолежащие грани параллелепипедаравны и лежат в параллельныхплоскостях.
2) диагоналипараллелепипедапересекаются в однойточке и делятсяэтойточкой пополам.
Сегоднямыподробнейрассмотримпрямоугольныйпараллелепипед и выясним, какимисвойствами он обладает.
Давайте представим себе комнату, имеющую форму прямоугольногопараллелепипеда. Если говорить о ееразмерах, то обычноупотребляют слова «длина», «ширина» и «высота». Имея в виду длинытрехребер с общейвершиной. В геометрииэти три величиныобъединяютсяобщимназванием: измеренияпрямоугольногопараллелепипеда.

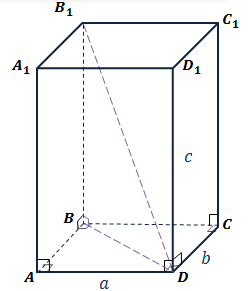
На рисункеизображенпрямоугольныйпараллелепипед ABCDA1B1C1D1.
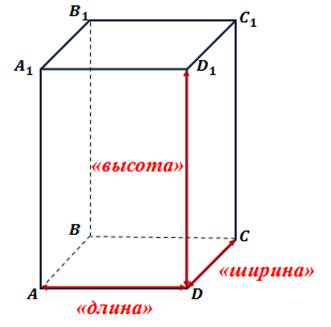
В качестве его измеренийможновзять, например, длиныребер DA, DC и DD1, все эти ребра имеютобщую вершину D.
Каквы уже знаете у прямоугольника два измерения – длина и ширина.
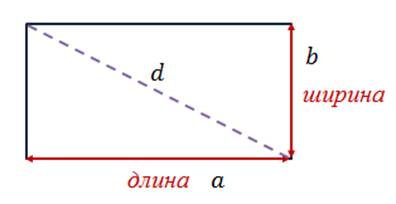
При этомнапомню, 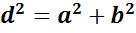 .
.
Оказывается, чтоаналогичнымсвойствомобладает и прямоугольныйпараллелепипед: квадрат диагоналипрямоугольногопараллелепипедаравенсуммеквадратовтрех его измерений.
Рассмотримпрямоугольныйпараллелепипед 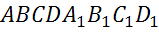 . И докажем, что
. И докажем, что 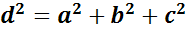 – диагональпараллелепипеда, а, b и c – ребра, имеющиеобщую вершину.
– диагональпараллелепипеда, а, b и c – ребра, имеющиеобщую вершину.
Пусть 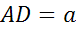 ,
, 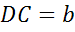 ,
, 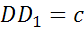 .
.
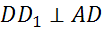 ,
, 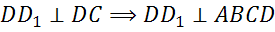
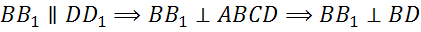
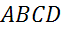 – прямоугольник.
– прямоугольник.
Из 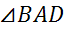 по теоремеПифагораимеем
по теоремеПифагораимеем 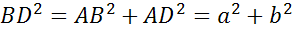 .
.
Из 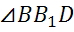 по теоремеПифагораимеем
по теоремеПифагораимеем 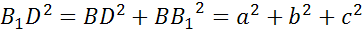 .
.
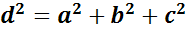
Замечание. Данноеутверждениеназывают пространственнойтеоремойПифагора.
Рассмотримеще одно свойство, иллюстрирующееаналогиюмеждупрямоугольником и прямоугольнымпараллелепипедом. Мызнаем, чтоплощадьпрямоугольникаравнапроизведению его измерений. 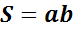
Оказывается, чтоаналогичноеутверждение справедливо и для прямоугольногопараллелепипеда: объемпрямоугольногопараллелепипедаравенпроизведениютрех его измерений.
Для доказательстваэтогоутверждениявоспользуемся принципом Кавальери.
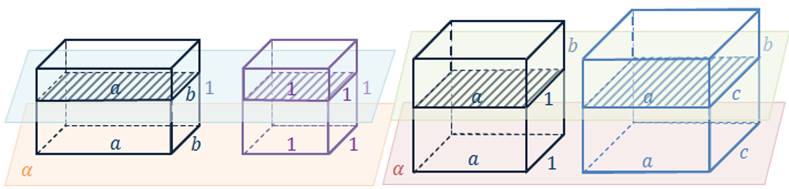
Рассмотримсначалапрямоугольныйпараллелепипед с измерениями а, b, 1 и куб с ребром 1, «стоящие» на плоскости α. Этот куб являетсяединицейизмеренияобъемов, т. е. его объемравен 1. Любаясекущаяплоскость, параллельнаяплоскости α, дает в качествесечения куба квадрат площадиравной 1, а в качествесечениярассматриваемогопараллелепипеда – прямоугольникплощадиравнойпроизведениюab. Следовательно, согласно принципу Кавальери, объемэтогопараллелепипеда в а на b раз большеобъема куба, т. е. равенab.
Рассмотримтеперь два прямоугольныхпараллелепипеда: один с измерениями а, b, 1, а другой – с измерениями а, b, c, «стоящие» на плоскости α так, как показано на рисунке. Объемпервогопараллелепипеда, какбыло доказано, равенab. Докажем, чтообъемвторогопараллелепипедаравенabc.
Любаясекущаяплоскость, параллельнаяплоскости α, дает в качествесеченияпервогопараллелепипедапрямоугольникплощадиравной 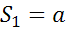 , а в качествесечениявторого – прямоугольникплощадиравнойпроизведению
, а в качествесечениявторого – прямоугольникплощадиравнойпроизведению 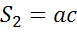 . Поэтомуобъемвторогопараллелепипеда в c раз большеобъемапервого и, следовательно, равен
. Поэтомуобъемвторогопараллелепипеда в c раз большеобъемапервого и, следовательно, равен 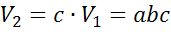 . Что и требовалосьдоказать.
. Что и требовалосьдоказать.
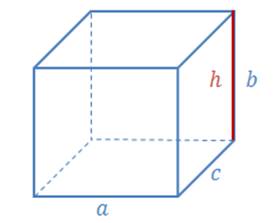
В прямоугольномпараллелепипеде с измерениями а, b, c, изображенном на рисунке, площадь 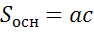 , а высота
, а высота 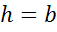 . Поэтому формулу
. Поэтому формулу 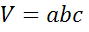 можнозаписать в виде
можнозаписать в виде 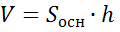 , т. е. объемпрямоугольногопараллелепипедаравенпроизведениюплощадиоснования на высоту.
, т. е. объемпрямоугольногопараллелепипедаравенпроизведениюплощадиоснования на высоту.
Оказывается, чтотакая же формула имеетместо для любойпризмы: объемпризмыравенпроизведениюплощадиоснования на высоту.
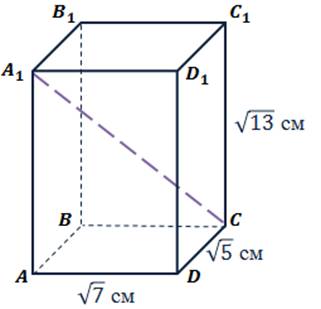
Задача. 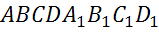 прямоугольныйпараллелепипед. Определитечемуравнадиагональ
прямоугольныйпараллелепипед. Определитечемуравнадиагональ 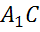 , еслипараллелепипедимеетизмерения
, еслипараллелепипедимеетизмерения 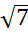 см,
см, 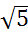 см и
см и 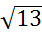 см.
см.
Решение.
Напомню, что квадрат диагоналипрямоугольногопараллелепипедаравенсуммеквадратовтрех его измерений.
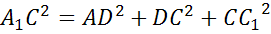
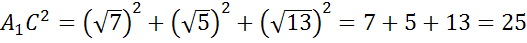
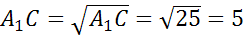 (см)
(см)
Ответ: 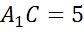 (см).
(см).
Задача. 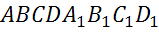 прямоугольныйпараллелепипед, основание
прямоугольныйпараллелепипед, основание 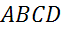 – квадрат. Объем
– квадрат. Объем 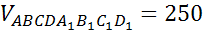 см3. Определитевысотупрямоугольногопараллелепипеда, если
см3. Определитевысотупрямоугольногопараллелепипеда, если 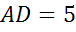 см.
см.
Решение.
На этомурокемы доказали, чтообъемпрямоугольногопараллелепипедаравенпроизведениюплощадиоснования на высоту. Выразимизформулывысоту.
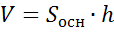
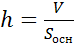
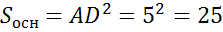 (см2)
(см2)
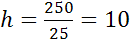 (см)
(см)
Ответ: 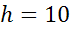 (см).
(см).
Подведемитогиурока. На этомурокемыподробнорассмотрелипрямоугольныйпараллелепипед. И выяснили, чтопрямоугольныйпараллелепипедобладаетсвойствами, иллюстрирующимианалогию с прямоугольником. А именно квадрат диагоналипрямоугольногопараллелепипедаравенсуммеквадратовтрех его измерений. И объемпрямоугольногопараллелепипедаравенпроизведениютрех его измерений. А такжеобъемпрямоугольногопараллелепипедаможновычислитькакпроизведениеплощадиоснования на высоту.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|