
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Собственные векторы и собственные значения
Собственные векторы и собственные значения
линейного оператора
(17марта, 4гр. и 5гр. 1-го курса)
Поставим перед собой задачу: Для данного оператораА: Е 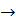 Е с матрицей
Е с матрицей
Ае= 
найтитакиечислаλ, чтобывыполнялосьравенствоАx =λ xдля некоторого ненулевого вектораx.
Координаты вектора x в базисе е обозначим x1, x2, x3. Тогда должно выполняться равенство
 ·
· 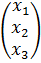 = λ ·
= λ · 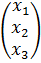
Это равносильно тому, что
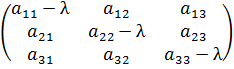 ·
· 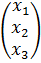 =
= 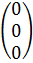 (1)
(1)
Если раскрыть это равенство, то получится система однородная система линейных уравнений с матрицей, равной Ае− λ Е.
Если определитель этой матрицы ≠ 0, то по правилу Крамера эта система имеет единственное нулевое решение, которое даст нулевой вектор с такими координатами. Это не будет решением задачи.
Если же определитель 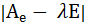 = 0, то ранг этой матрицы окажется меньше, чем 3, и система будет иметь ненулевые решения. Значит, в этом случае, решая систему (1), мы тем самым решим поставленную задачу.
= 0, то ранг этой матрицы окажется меньше, чем 3, и система будет иметь ненулевые решения. Значит, в этом случае, решая систему (1), мы тем самым решим поставленную задачу.
Итак, поставленная задача имеет решение тогда и только тогда, когда выполняется условие  = 0.
= 0.
Все такие значения  называются собственными значениями оператораА,
называются собственными значениями оператораА,
а ненулевые векторыx, для которых Аx =λ x, называются собственными векторами этого операторас собственным значением λ.
Пример. Ае = 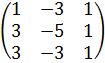 .
.
 =
= 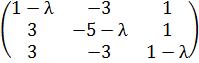 =
=
= (  )·(
)·( 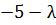 )·(
)·( 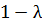 )
)  9
9 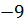 +3·(
+3·(  ) +3·(
) +3·( 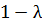 ) +9·(
) +9·( 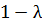 )=
)=
= (1 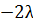 +λ 2)·(
+λ 2)·( 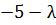 ) + 9 – 9λ =
) + 9 – 9λ =
= − λ 3 − 3λ 2 + 4= − (λ 3 +3λ 2 – 4).
| − 4 | ||||
| 0 |
Таким образом, 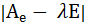 = 0 тогда и только тогда, когда λ 3 +3λ 2 – 4=0. Хорошо виден один корень этого уравнения:
= 0 тогда и только тогда, когда λ 3 +3λ 2 – 4=0. Хорошо виден один корень этого уравнения: 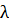 =1. Делим многочлен на (
=1. Делим многочлен на ( 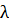 − 1) по схеме Горнера:
− 1) по схеме Горнера:
Поэтому λ 3 +3λ 2 – 4= ( 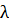 − 1)· (λ 2 +4λ + 4) = (
− 1)· (λ 2 +4λ + 4) = ( 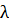 − 1)· (λ +2)2.
− 1)· (λ +2)2.
Все корни этого многочлена: 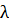 =1
=1 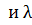 =− 2. Это все собственные значения данного оператора.
=− 2. Это все собственные значения данного оператора.
Решая систему (1) для собственного значения 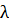 =1, а потом для собственного значения
=1, а потом для собственного значения 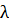 = − 2, найдём координаты всех собственных векторов данного оператора.
= − 2, найдём координаты всех собственных векторов данного оператора.
1) 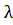 =1
=1  ·
· 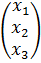 =
= 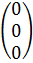
Так как определитель матрицы равен нулю, то её ранг равен 2. Поэтому одна строка линейно выражается через другие, например вторая. Вычеркнем её, последнюю разделим на 3, поменяем местами с первой и запишем соответствующую систему
 −
− 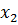 + 0·
+ 0· 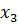 = 0
= 0
−  +
+ 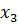 = 0
= 0
Положим 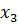 = С3, или, чтобы удобнее было вычислять,
= С3, или, чтобы удобнее было вычислять, 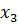 = 3С3.
= 3С3.
Тогда 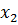 = С3,
= С3,  = С3.
= С3.
Общее решение системы имеет вид (x1, x2, x3) = (С3, С3, 3С3), где С3Î R.
По этим координатам записываем векторы и берём только ненулевые:
x= (С3, С3, 3С3)e, где С3Î R, С3≠ 0. Это все собственные векторы оператораА с собственным значением 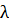 =1.
=1.
2) 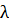 =− 2.
=− 2. 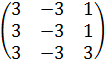 ·
· 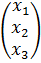 =
= 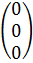
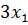 − 3
− 3 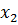 +
+ 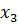 = 0
= 0  −
− 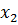 +
+ 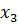 = 0
= 0
 −
− 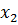 +
+ 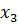 = 0 или − 2
= 0 или − 2 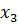 =0.
=0.
Запишем систему в ступенчатом виде
 +
+ 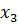 −
− 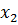 = 0
= 0
− 2 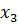 =0
=0
Получаем общее решение(x1, x2, x3) = (С2, С2, 0), где С2Î R.
По этим координатам записываем векторы и берём только ненулевые:
x= (С2, С2, 0)e, где С2Î R, С2≠ 0. Это все собственные векторы оператораА с собственным значением 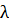 = − 2.
= − 2.
Всё рассмотренное перенесём на случай линейного оператораА: Е 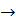 Е, действующего в пространстве произвольной размерности. Тогда
Е, действующего в пространстве произвольной размерности. Тогда
Ае=  Ае−
Ае− 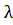 E=
E= 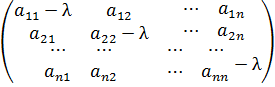
Определение. Собственным вектором линейного оператораА: Е  Е называется такой ненулевой вектор xÎ E, чтоАx = λ x. При этом число λ называется собственным значением этого вектора, а также собственным значением этого оператора.
Е называется такой ненулевой вектор xÎ E, чтоАx = λ x. При этом число λ называется собственным значением этого вектора, а также собственным значением этого оператора.
Теорема. Число λ является собственным значением оператораА: Е  Е тогда и только тогда, когда определитель
Е тогда и только тогда, когда определитель 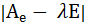 = 0.
= 0.
Определение. Многочлен от переменной λ, равный определителю
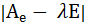 , называется характеристическим многочленом оператора А.
, называется характеристическим многочленом оператора А.
Таким образом,
1. Все собственные значения оператораА− это все вещественные корни его характеристического многочленаp(λ ) = 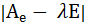 .
.
2. Если λ 0− собственное значение оператораА, то соответствующие ему собственные векторы строятся по всем ненулевым решениям однородной линейной системы, матрица которой совпадает с матрицей 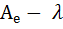 0Е. Эти решения – координаты собственных векторов в базисе е.
0Е. Эти решения – координаты собственных векторов в базисе е.
Замечания.
1) Характеристический многочлен p(λ ) = 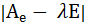 не зависит от выбора базиса. Действительно, при другом базисе fтого же пространства, будем иметь:
не зависит от выбора базиса. Действительно, при другом базисе fтого же пространства, будем иметь:
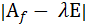 =
= 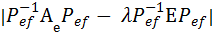 =
= 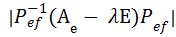 =
=
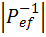 ·
· 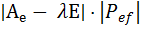 =
= 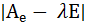 =p(λ ).
=p(λ ).
2) В случае n=3 характеристический многочлен может быть вычислен по матрице оператора
Ае= 
с помощью формулы
p(λ ) = − (λ 3 – (  )·λ 2 +(
)·λ 2 +( 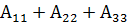 )·λ −
)·λ − 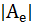 ).
).
Пример. Для рассмотренного выше оператора с матрицей
Ае = 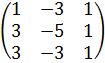
Сумма (  ) = 1− 5 + 1 = 3;
) = 1− 5 + 1 = 3;
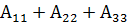 =
= 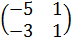 +
+ 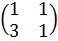 +
+ 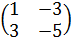 = − 2 − 2 + 4 = 0,
= − 2 − 2 + 4 = 0,
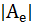 = − 5− 9− 9+ 15 + 3 + 9 = 4
= − 5− 9− 9+ 15 + 3 + 9 = 4
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|