- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
«ЭЛЕКТРИЧЕСКИЕ ЦЕПИ» 2 страница
При протекании переменного тока i(t) через катушку индуктивности, со- стоящей из w витков, возбуждается переменный магнитный поток Ф(t), который в соответствии с законом электромагнитной индукции наводит в ней же ЭДС само- индукции eL = – w dФ/dt = – Ldi/dt. Следовательно, индуктивность в цепи перемен- ного тока влияет на величину протекающего тока как сопротивление. Соответст- вующая расчетная величина называется индуктивным сопротивлением и обознача- ется ХL и измеряется так же, как и активное сопротивление – в Омах.
Чем выше частота переменного тока, тем больше ЭДС самоиндукции и тем больше индуктивное сопротивление ХL = wL =2pf L. Величина w =2pf называется угловой частотой переменного тока.
В цепи постоянного тока в установившемся режиме индуктивность не влия- ет на режим работы цепи, так как ЭДС самоиндукции равна нулю.
Поскольку ЭДС самоиндукции возникает только при изменении тока, то и максимальные значения ЭДС наступают при максимальной скорости изменения тока в катушке, то есть при прохождении тока через нуль. Поэтому на участке цепи с индуктивностью ЭДС самоиндукции по времени отстает от тока на четверть периода или на p/2 электрических радиана. Напряжение на индуктивности, будучи противоположным ЭДС, наоборот, опережает ток на четверть периода или на p/2 электрических радиана. Если по катушке проходит ток, мгновенное значение которого i(t)=IM sin 2pft, то мгновенное значение напряжения на индуктивности uL(t)=UM sin (2pft + p/2) = ХL. IM sin (2pft + p/2). Когда напряжение, изменяясь синусоидально, достигает максимума, ток в это мгновение равен нулю. Если напряжение на зажимах элемента цепи опережает ток на p/2 радиана, то говорят, что такой элемент представляет собой идеальную катушку индуктивности или чисто реактивное индуктивное сопротивление ХL. Это сопротивление учитывает реакцию электрической цепи на изменение магнитного поля в индуктивности и является линейной функцией частоты.
При включении в цепь переменного тока реальной катушки (рис. 1), обладающей кроме индуктивности L и некоторым значением активного сопротивления R, ток отстает по фазе от напряжения на некоторый угол j < p/2, который легко определяется из треугольника сопротивлений (рис. 3):
tgj = ХL / R.
Для такого участка электрической цепи уравнение на основании второго закона Кирхгофа имеет вид:
u = uR + uL= Ri + Ldi/dt.
В напряжении, подведенном к реальной катушке, условно можно выделить две составляющих: падение напряжения Ri на активном сопротивлении, обычно называемое активной составляющей приложенного напряжения, и напряжение на идеальной индуктивности uL= Ldi/dt, называемое реактивной составляющей приложенного напряжения. Фазовые соотношения между этими составляющими, приложенным напряжением и протекаемым током обычно иллюстрируются векторной диаграммой для их действующих значений (рис. 2). Из векторной диа-
|
|
|
|
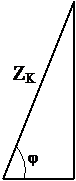
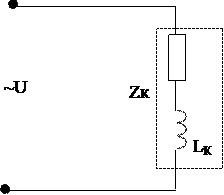
 R = Z cosj, ХL=Zsinj, j = arctg ХL / R.
R = Z cosj, ХL=Zsinj, j = arctg ХL / R.
ХL
UL
Рис. 1
UR
Рис. 2
RK
Рис. 3
Закон Ома для цепи, по которой протекает переменный ток, записывается в виде I = U / Z.
Из рассмотренного следует важный вывод: сопротивления в цепи пере- менного тока складываются в общем случае геометрически . Например, если у катушки R=3 Ома и ХL = 4 Ома, то Z = 5 Ом.
Емкость, измеряемая в фарадах (Ф), характеризует способность элемента электрической цепи или конденсатора накапливать энергию электрического поля. В реальной цепи емкость существует не только в конденсаторах, как элементах предназначенных специально для использования их емкости, ноли между провод- никами, между витками катушек (межвитковая емкость), между проводом и землей или каркасом электротехнического устройства. Однако в схемах замещения приня- то, что емкостью обладают только конденсаторы.
В конденсаторе, точнее в диэлектрике, разделяющем пластины или провод- ники конденсатора, может существовать ток электрического смещения, в точности равный току проводимости в проводниках, присоединенных к обкладкам конден- сатора: i = dq / dt, где q – заряд на обкладках конденсатора, измеряемый в кулонах и пропорциональный напряжению на конденсаторе UC:
q = C UC, и при С = сonst dq = С dUC.
Тогда ток, проходящий через конденсатор, i = C dUC / dt, а энергия элек- трического поля, запасаемая в конденсаторе при возрастании напряжения, W = C
U 2 / 2.
C
Очевидно, что при постоянном напряжении dUC / dt = 0 и постоянный ток
через конденсатор проходить не может.
При изменении напряжения на обкладках конденсатора через него протека- ет емкостной ток. Чем быстрее изменяется напряжение, тем больше емкостной ток. Если приложить к конденсатору переменное синусоидальное напряжение, то через конденсатор потечет переменный синусоидальный ток, сдвинутый по фазе на p/2 по отношению к напряжению. Это происходит потому, что емкостной ток достига- ет максимального значения при максимальном изменении напряжения, т. е. при прохождении напряжения через нуль. Ток при этом опережает напряжение по фазе на p/2. Если мгновенное значение тока, протекаемого через конденсатор i(t)=IM sin 2pft, то мгновенное значение напряжения на нем
uС(t)=UM sin(2pft - p/2)=XC IM sin (2pft - p/2),
где XC – реактивное емкостное сопротивление. Векторная диаграмма для участка электрической цепи, содержащей конденсатор, изображена на рис. 4.
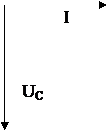 Величина XC = 1/2pfC = 1/wC = UCm / Im = UC / I называется реактивным емкостным сопротивлением. Это сопротивление учиты- вает реакцию электрической цепи на изменение электрического поля в конденсаторе и является обратно пропорциональной функцией час- тоты.
Величина XC = 1/2pfC = 1/wC = UCm / Im = UC / I называется реактивным емкостным сопротивлением. Это сопротивление учиты- вает реакцию электрической цепи на изменение электрического поля в конденсаторе и является обратно пропорциональной функцией час- тоты.
Закон Ома для участка электрической цепи с конденсатором I
= UC / XC, где I – действующее значение тока, протекаемого через конденсатор, UC – действующее значение напряжения на конденсато- ре.
Рис. 4
В электрических цепях переменного тока используют понятия активной, реактивной и полной мощности.
Активная мощность P, измеряемая в ваттах (Вт), равна произведению дей- ствующего значения напряжения U на действующее значение ток I и на сosj, на- зываемый коэффициентом мощности, или произведению квадрата действующего значения тока на активное сопротивление:
P = UI сosj = I2 R.
Реактивная мощность Q, измеряемая в вольт-амперах реактивных (Вар),
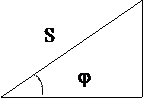 равна произведению действующего значения напряжения U
равна произведению действующего значения напряжения U
на действующее значение тока I и на sinj или произведению квадрата действующего значения тока на реактивное сопро- тивление:
Q = UI sinj = I2 Х.
Полная мощность S, измеряемая в вольт-амперах (ВА), равна произведению действующего значения тока I на дейст- вующее значение напряжения U:
S = U I =Ö P2 + Q2 .
Q
Рис. 5
Соотношения этих мощностей иллюстрируются треугольником мощностей
(рис. 5).
3. Порядок выполнения работы
Ознакомиться с лабораторной установкой (модуль питания, модуль ввода, модуль резисторов, модуль реактивных элементов и модуль мультиметров, компьютер).
Установить на мультиметре режим измерения сопротивления, подклю- чить его выводы параллельно резистору R1 модуля резисторов и включив электро- питание стенда (выключатель QF1 модуля питания) провести измерение значений сопротивления R1. Результаты измерений записать в табл. 1.
Таблица 1
| Установлено | 5 Ом | 10 Ом | 20 Ом | 30 Ом | 40 Ом | 50 Ом |
| Измерено |
Аналогично п. 3. 2 провести измерение активного сопротивления RК ре- альной катушки индуктивности ZК. Результат измерения записать в табл.. 2.
Таблица 2
| RК, Ом | U, B | I, A | φ, град. | Т, сек | f=1/Т, Гц | ZК = U/I, Ом | ХК, Ом | L= ХК /2π f, Гн |
Собрать электрическую цепь для исследования катушки индуктивности
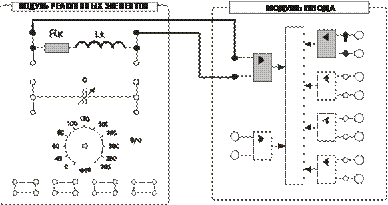
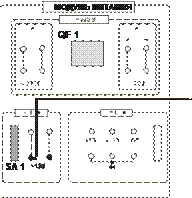

 (рис. 6). Предъявить схему для проверки преподавателю.
(рис. 6). Предъявить схему для проверки преподавателю.
| А3 | ДТ1 |
| ||
| А1 | ||||
| ДН1 | ||||
| А4 | ДТ2 | |||
| ПК | ||||
| А5 | ДТ3 | |||
| ДН2 | А2 | |||
| SA 2 | А6 | ДТ4 |
Рис. 6
Включить питание компьютера, открыть окно лабораторной работы №3
«Экспериментальное определение параметров цепей переменного тока». Запустить программу в работу, нажатием кнопки «Пуск»  или командой главного меню
или командой главного меню
«Управление – Пуск» или горячей клавишей F5.
Включить электропитание стенда (выключатель QF1, SA2 и SA1 модуля пи- тания) и записать табл. 2 результаты измерений действующих значений напряже- ния и тока. Снять осциллограммы напряжения и тока в цепи, нарисовав их на од- ной координатной плоскости, определить по ним амплитуды, период и частоту из- меряемого напряжения и тока, а также угол сдвига фаз φ между ними. Остановить программу, нажатием кнопки «Стоп»  или командой главного меню «Управление
или командой главного меню «Управление
– Стоп» или горячей клавишей F6.
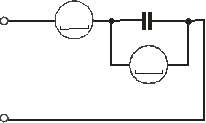 Собрать электрическую цепь для определения фактической величины емкости конденсатора модуля реактивных элементов (рис. 7). Для измерения тока и напряжения использовать цифровые приборы измерительного модуля в режиме измерения переменного тока.
Собрать электрическую цепь для определения фактической величины емкости конденсатора модуля реактивных элементов (рис. 7). Для измерения тока и напряжения использовать цифровые приборы измерительного модуля в режиме измерения переменного тока.
После проверки цепи преподавателем включить электропитание (выключатели QF, и SA1) и измерить напряжение и ток в цепи. Результаты занести в табл. 3. Выключить электропитание.
Рассчитать величину емкостного сопротивления XС и величину фактической емкости конденсатора Сфакт, учитывая, что частота напряжения 50 Гц.
~12 В
А
РА C
V
РV
Таблица 3 Рис. 7
| Cзад, мкФ | U, B | I, A | XС = U/I, Ом | Сфакт= 1/ 2π f XС, мкФ |
4. Содержание отчета
Отчет по работе должен содержать:
а) наименование работы и цель работы; б) электрические схемы опытов;
в) осциллограммы и таблицы с результатами опытов и вычислений; г) расчетные соотношения;
д) построенные в масштабе векторные диаграммы для резистора, реальной катушки и конденсатора;
е) выводы по работе.
5. Контрольные вопросы
1. В каких единицах измеряется ток, напряжение, сопротивление?
2. Что такое Ом, Ампер, Вольт?
3. Что такое «полное сопротивление»?
4. Что такое «активное сопротивление»?
5. Что такое «реактивное сопротивление» и как оно определяется?
6. Какая связь между полным, активным и реактивным сопротивлениями цепи переменного тока?
7. Как формулируется закон Ома для цепи переменного тока?
8. Может ли через конденсатор протекать постоянный ток?
9. Каковы углы сдвига фаз между напряжением и током на резисторе, ре- альной катушке и конденсаторе?
4. Работа № 4 ЭЛЕКТРИЧЕСКАЯ ЦЕПЬ ПЕРЕМЕННОГО ТОКА С ПОСЛЕДОВАТЕЛЬНЫМ СОЕДИНЕНИЕМ ЭЛЕМЕНТОВ
1. Цель работы
Приобретение навыков сборки простых электрических цепей, измерение напряжений на отдельных участках цепи, изучение свойств цепей при последова- тельном соединении активных и реактивных элементов, знакомство с явлением ре- зонанса напряжений, построение векторных диаграмм.
2. Пояснения к работе
Электрическая цепь синусоидального переменного тока с последовательным соединением резистора с активным сопротивлением R, реальной катушки индук- тивности с полным сопротивлением ZK (RK, XK) и конденсатора с емкостным сопро- тивлением XC (рис. 1) описывается уравнением, записанным по второму закону Кирхгофа для мгновенных значений напряжений на этих элементах:
uR + uK + uC = u(t)
или в геометрической форме для векторов действующих значений этих напряже- ний ⎯ UR + ⎯ UK + ⎯ UC = ⎯ U
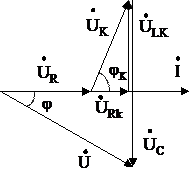
Последнее соотношение говорит о том, что вектор действующего значения напряжения, приложенного к такой цепи, равен геометрической сумме векторов напряжений на отдельных её участках (рис. 2).
R
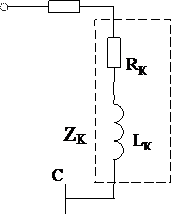
 XL
XL
Рис. 1
Рис.. 2
X
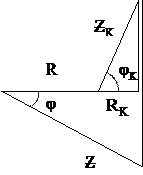
Рис. 3
Из анализа векторной диаграммы для такой цепи следует, что величина входного напряжения
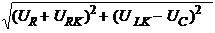
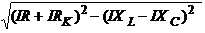
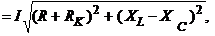 U = =
U = =
где URК, ULК – соответственно активная и реактивная составляющие напряжения на катушке, RK, XL – активное и реактивное индуктивное сопротивление катушки ин- дуктивности.
 Следовательно, действующее значение тока в этой цепи на основании зако-
Следовательно, действующее значение тока в этой цепи на основании зако-
на Ома можно определить как I= U / Z = U /
(R + RK )2 + ( X L - XC )2,
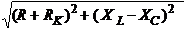
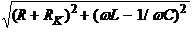 где Z = = – полное сопротивление
где Z = = – полное сопротивление
цепи с последовательным соединением резистора, реальной катушки индуктивно-
сти и конденсатора, которое легко определяется из многоугольника сопротивлений
(рис. 3).
Угол сдвига фаз между входным синусоидальным напряжением U и по- требляемым такой цепью током I определяется из треугольника сопротивлений
tgj = (wL – 1/wC) / (R + RK).
Если wL > 1/wC и угол j > 0, вся цепь ведет себя как цепь с активным со- противлением и идеальной индуктивностью. Говорят, что в этом случае цепь носит активно-индуктивный характер.
Если wL < 1/wC и угол j < 0, вся цепь ведет себя как цепь с активным со- противлением и емкостью. Говорят, что в этом случае цепь носит активно- емкостной характер.
Если в цепи реактивное сопротивления равны (wL = 1/wC), то угол j = 0. При этом реактивная составляющая напряжения на индуктивности и напряжение на конденсаторе полностью себя компенсируют. Цепь ведет себя, как будто реак- тивные сопротивления в ней отсутствуют и ток достигает наибольшего значения, поскольку ток ограничивается только эквивалентным активным сопротивлением цепи RЭ = R +RK.
Это означает, что в цепи имеет место резонанс, называемый в данном слу- чае резонансом напряжений. Резонанс напряжений можно получить либо измене- нием частоты источника питания, либо подбором значения величины С = 1/w0 2L, где w0 = Ö 1/LC – резонансная частота цепи.
3. Порядок выполнения работы
Ознакомиться с лабораторной установкой (компьютер, модуль ввода, модуль питания, модуль резисторов, модуль реактивных элементов).
В соответствии со схемой по рис. 4 нарисовать электрическую схему исследуемой цепи. Собрать электрическую цепь (рис. 4), установив заданные пре- подавателем значений сопротивления резистора R1 и емкости конденсатора C. Подключить собранную цепь к источнику питания ~12В (модуль питания). Под- соединить параллельно конденсатору дополнительный проводник (исключив этим конденсатор из цепи). Предъявить схему для проверки преподавателю.
Включить компьютер и открыть окно «Лабораторная работа № 4. Элек- трическая цепь переменного тока с последовательным соединением элементов». Запустить программу в работу, нажатием кнопки «Пуск»  или командой главно- го меню «Управление – Пуск» или горячей клавишей F5.
или командой главно- го меню «Управление – Пуск» или горячей клавишей F5.
Включить электропитание стенда (выключатель QF1, SA2 и SA1 модуля питания). Произвести измерения указанных в таблице 1 величин в цепи с последо- вательным соединением резистора R1 и индуктивной катушки ZK. По осцилло- граммам определить угол сдвига фаз φ между приложенным на входе цепи напря- жением и током и сделать вывод о характере цепи. Результаты измерений занести в табл. 1. Зарисовать осциллограммы. Остановить программу. Выключить источ- ник переменного напряжения (SA1).
Таблица 1
| Схема | U, B | I, A | ±φ, град | UR, B | UK, B | UC, B |
| ZK, R | ||||||
| R, XC | ||||||
| R, ZK, XC1 | ||||||
| R, ZK, XC2 | ||||||
| R, ZK, XC3 |
Удалить проводник, включенный параллельно конденсатору. Подсое- динить дополнительный проводник параллельно индуктивной катушке (исключив этим вместо конденсатора индуктивную катушку из цепи). Предъявить схему для проверки преподавателю.
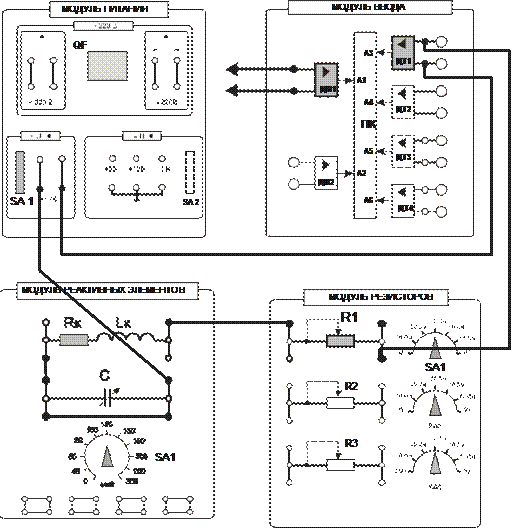 |
Рис. 4
Включить источник электропитания и произвести измерения указанных в таблице 1 величин для цепи с последовательным соединением резистора R и кон- денсатора С. По осциллограммам определить угол сдвига фаз между приложенным на входе цепи напряжением U и током I и сделать вывод о характере цепи. Резуль- таты измерений занести в табл. 1. Зарисовать осциллограммы. Выключить элек- тропитание, убрать дополнительный проводник.
В цепи с последовательным соединением резистора R1, индуктивной катушки ZK и конденсатора C изменяя величину емкости конденсатора с помощью переключателя SA1 модуля реактивных элементов, добиться наибольшего значе-
ния тока I, т. е. обеспечить состояние цепи близкое к резонансу напряжений. По ос- циллограммам определить угол сдвига фаз φ между приложенным на входе цепи напряжением U и током I и сделать вывод о характере цепи. Зарисовать осцилло- граммы. Результаты измерений занести в табл. 1.
Уменьшая и увеличивая величину емкости конденсатора C (от резонанс- ного значения) провести измерения указанных в таблице величин для двух состоя- ний цепи. По осциллограммам определить угол сдвига фаз φ между приложенным на входе цепи напряжением U и током I и сделать вывод о характере цепи. Резуль- таты измерений занести в табл. 1. Зарисовать осциллограммы. Выключить элек- тропитание стенда. Остановить программу, нажатием кнопки «Стоп»  или ко- мандой главного меню «Управление – Стоп» или горячей клавишей F6.
или ко- мандой главного меню «Управление – Стоп» или горячей клавишей F6.
Для цепи с последовательным соединением трех элементов (R, ZK, C) по результатам измерений определить величины, указанные в табл. 2.
Таблица 2
| S, ВА | SR, ВА | SK, ВА | SC, ВА | P, Вт | PR, Вт | PK, Вт | QK, ВАр | QC, ВАр | RЭ, Ом | XЭ, Ом | Z, Ом |
По результатам измерений построить для исследованных цепей в мас- штабе векторные диаграммы.
Сделать вывод о применении 2-го закона Кирхгофа в цепях перемен- ного тока.
4. Содержание отчета
Отчет по работе должен содержать:
а) наименование работы и цель работы; б) схему исследуемой цепи;
в) осциллограммы;
г) таблицы с результатами опытов и вычислений; в) расчетные соотношения;
е) векторные диаграммы; ж) выводы по работе.
5. Контрольные вопросы
1. Что такое активная, реактивная и полная мощности в цепи переменного
тока?
2. Какая взаимосвязь между полной, активной и реактивной мощностями?
3. Что такое «коэффициент мощности»?
4. Как вычислить полное сопротивление катушки, если известны её актив-
ное сопротивление, индуктивность и частота сети?
5. Как вычислить полное сопротивление цепи с последовательным соедине- нием резистора, реальной катушки и конденсатора?
6. От чего зависит угол сдвига фаз между напряжением и током на участке электрической цепи переменного тока?
7. Что такое «треугольник сопротивлений»?
8. Чему равны реактивное сопротивление цепи и реактивная мощность цепи при резонансе? Каков при этом характер цепи?
5. Работа № 5. ЭЛЕКТРИЧЕСКА ЦЕПЬ ПЕРЕМЕННОГО ТОКА С ПАРАЛЛЕЛЬНЫМ СОЕДИНЕНИЕМ ЭЛЕМЕНТОВ
1. Цель работы
Ознакомиться с особенностями электрической цепи с параллельным соеди- нением активных и реактивных элементов, явлением резонанса токов, способом повышением коэффициента мощности индуктивного потребителя, применением 1- го закона Кирхгофа в цепях переменного тока.
2. Пояснения к работе
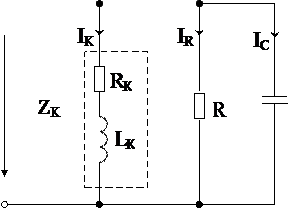
При параллельном соединении элементов получают разветвленную цепь (рис. 1). При параллельном соеди- нении элементов токи в отдельных вет- вях, зависят только от напряжения ис- точника питания и полного сопротив- ления каждой ветви. При этом ток в ветви с резистором IR совпадает по фазе с напряжением источника, ток в ветви с катушкой IK отстает по фазе от напря- жения источника питания на угол j, за- висящий от активного и реактивного сопротивления реальной катушки ин-

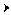 I
I
U C
Рис. 1
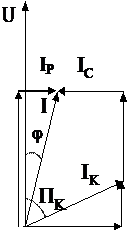 дуктивности. Ток в ветви с конденсатором IC опережает напряжение источника пи- тания на 90° (рис. 2). В соответствии с первым законом Кирхгофа общий ток I, по- требляемый такой цепью от источника питания, определя-
дуктивности. Ток в ветви с конденсатором IC опережает напряжение источника пи- тания на 90° (рис. 2). В соответствии с первым законом Кирхгофа общий ток I, по- требляемый такой цепью от источника питания, определя-
ется геометрической суммой токов отдельных ветвей:
⎯ I = ⎯ IR +⎯ IK +⎯ IC.
Геометрическое построение для определения вели-
чины и фазы общего тока представлено на рис. 2, где обо- значено
IКА, IА – активные составляющие тока в ветви с ка- тушкой и общего тока;
IКР, IР – реактивные составляющие тока в ветви с IA
катушкой и общего тока.
Под активной составляющей тока понимают ус- ловную составляющую этого тока, совпадающую по фазе с приложенным к этому участку напряжением. Под реак- тивной составляющей тока – составляющую, расположен- ную под 90° к приложенному напряжению. Следует пом-
IR
IKР
Рис. 2
нить, что активная и реактивная составляющие тока – это условные величины, не имеющие физического смысла в последовательной схеме замещения.
Из векторной диаграммы следует, что
IА = IR + IКА, IР = IКР – IC .
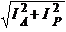 Следовательно, величина общего тока I = ,
Следовательно, величина общего тока I = ,
а угол сдвига фаз между общим током и приложенным напряжением
tgj = IР / IА= (IКР – IC) / (IR + IКА).
Данная векторная диаграмма построена в предположении, что емкостной ток IC оказался меньше реактивной индуктивной составляющей тока в катушке IКР. Поэтому общий ток отстает по фазе от напряжения. Такая цепь носит активно- индуктивный характер. Если бы емкостной ток IC был больше реактивной индук- тивной составляющей тока в катушке IКР, то ток, потребляемый цепью из сети опережал по фазе приложенное напряжение и цепь носила бы активно-емкостной характер.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|