Хелпикс

Главная

Контакты

Случайная статья



Планиметрия



 

1. а) Ре­ши­те урав­не­ние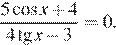

б) Най­ди­те все корни этого уравнения, при­над­ле­жа­щие от­рез­ку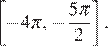

2. Ре­ши­те уравнение: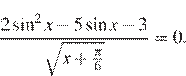

3. Решите урав­не­ние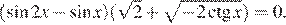

4. Решите урав­не­ние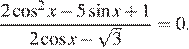

5. а) Ре­ши­те урав­не­ние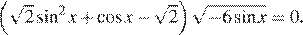

 

б) Най­ди­те все корни этого уравнения, при­над­ле­жа­щие от­рез­ку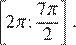

6. Решите уравнение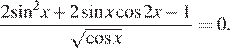

7. Ре­ши­те уравнение: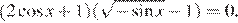

8. Решите уравнение

9. а) Ре­ши­те урав­не­ние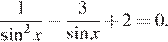

б) Ука­жи­те корни этого уравнения, при­над­ле­жа­щие от­рез­ку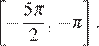

10. а) Ре­ши­те уравнение

 

б) Най­ди­те все корни этого уравнения, при­над­ле­жа­щие промежутку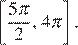

11. а) Ре­ши­те урав­не­ние .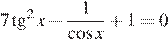

 

б) Най­ди­те все корни этого уравнения, при­над­ле­жа­щие про­ме­жут­ку .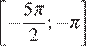

12. а) Ре­ши­те урав­не­ние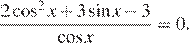

б) Най­ди­те все корни этого уравнения, при­над­ле­жа­щие от­рез­ку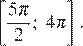

 

Планиметрия

1. Вершины ромба расположены на сторонах параллелограмма так, что сторороны ромба параллельны диагоналямпараллелограмма. Найдите отношение площади ромба к площади параллелограмма, если известно, что диагонали параллелограмматносятся как 2: 3

2.

 

В ос­но­ва­нии пра­виль­ной тре­уголь­ной приз­мы ABCA1B1C1 лежит тре­уголь­ник со сто­ро­ной 6. Вы­со­та приз­мы равна 4. Точка N — се­ре­ди­на ребра A1C1.

а) По­строй­те се­че­ние приз­мы плос­ко­стью BAN.

б) Най­ди­те пе­ри­метр этого сечения.

В ос­но­ва­нии пра­виль­ной тре­уголь­ной приз­мы ABCA1B1C1лежит тре­уголь­ник со сто­ро­ной 8. Вы­со­та приз­мы равна 3. Точка N — се­ре­ди­на ребра A1C1.

а) По­строй­те се­че­ние приз­мы плос­ко­стью BAN.

б) Най­ди­те пло­щадь этого сечения.

В пра­виль­ной че­ты­рех­уголь­ной пи­ра­ми­де PABCD, все ребра ко­то­рой равны 4, точка K ― се­ре­ди­на бо­ко­во­го ребра AP.

а) По­строй­те се­че­ние пи­ра­ми­ды плоскостью, про­хо­дя­щей через точку K и па­рал­лель­ной пря­мым PB и BC.

б) Най­ди­те пло­щадь сечения.

В пра­виль­ной че­ты­рех­уголь­ной пи­ра­ми­де PABCD, все ребра ко­то­рой равны 6, точка K ― се­ре­ди­на бо­ко­во­го ребра AP.

а) По­строй­те се­че­ние пи­ра­ми­ды плоскостью, про­хо­дя­щей через точку K и па­рал­лель­ной плос­ко­сти BCP.

б) Най­ди­те угол между плос­ко­стью се­че­ния и плос­ко­стью ос­но­ва­ния пирамиды.

На ребре пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да ABCDA1B1C1D1 взята точка E так, что A1E = 6EA. Точка T — се­ре­ди­на ребра B1C1. Известно, что AD = 12, AA1 = 14.

а) Докажите, что плос­кость ETD1 делит ребро BB1 в от­но­ше­нии 4: 3.

б) Най­ди­те пло­щадь се­че­ния па­рал­ле­ле­пи­пе­да плос­ко­стью ETD1.

В кубе ABCDA1B1C1D1 все рёбра равны 4. На его ребре BB1 от­ме­че­на точка K так, что KB = 3. Через точки K и C1 построена плос­кость α, па­рал­лель­ная пря­мой BD1.

а) Докажите, что A1P: PB1 = 2: 1, где P — точка пе­ре­се­че­ния плос­ко­сти α с реб­ром A1B1.

б) Най­ди­те угол на­кло­на плос­ко­сти α к плос­ко­сти грани BB1C1C.

На ребре AA1 пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да ABCDA1B1C1D1 взята точка E так, что A1E: EA = 5: 3, на ребре BB1 — точка F так, что B1F: FB = 5: 11, а точка T − се­ре­ди­на ребра B1C1. Известно, что AD = 10, AA1 = 16.

а) Докажите, что плос­кость EFT про­хо­дит через вер­ши­ну D1.

б) Най­ди­те пло­щадь се­че­ния па­рал­ле­ле­пи­пе­да плос­ко­стью EFT.

 

На ребре AA1 пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да ABCDA1B1C1D1 взята точка E так, что A1E: EA = 6: 1, на ребре BB1 — точка F так, что B1F: FB = 3: 4, а точка T — се­ре­ди­на ребра B1C1. Известно, что AD = 30, AA1 = 35.

а) Докажите, что плос­кость EFT про­хо­дит через вер­ши­ну D1.

б) Най­ди­те пло­щадь се­че­ния па­рал­ле­ле­пи­пе­да плос­ко­стью EFT.

.

Все рёбра пра­виль­ной тре­уголь­ной приз­мы ABCA1B1C1 имеют длину 6. Точки M и N— се­ре­ди­ны рёбер AA1 и A1C1 соответственно.

а) Докажите, что пря­мые BM и MN перпендикулярны.

б) Най­ди­те угол между плос­ко­стя­ми BMN и ABB1.



  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.