на тему: Генератор случайных величин

Министерство образования и науки Российской Федерации

Санкт-Петербургский государственный политехнический университет

Институт информационных технологий и управления

Кафедра систем и технологий управления

Реферат

на тему: Генератор случайных величин

Выполнил: студент гр. 33503/3 Попов С. С.

Преподаватель: Смирнов Ю. М.

Санкт-Петербург

Содержание

1. Способы получения случайных чисел. 3

2. Характеристики ГСЧ. 5

3. Применение ГСЧ. 6

4. Генерирование равномерно распределенных случайных чисел. 9

5. Генерирование чисел с произвольным распределением. 12

6. Тестирование ГСЧ. 17

Библиографический список. 19

1. Способы получения случайных чисел

В достаточно часто находят применение последовательности чисел, выбранных случайным образом из некоторого множества. В качестве примеров задач, в которых используются случайные числа, можно привести следующие:

- тестирование алгоритмов;

- имитационное моделирование;

- некоторые задачи численного анализа;

- имитация пользовательского ввода.

Для получения случайных чисел можно использовать различные способы. В общем случае все методы генерирования случайных чисел можно разделить на аппаратные и программные. Устройства или алгоритмы получения случайных чисел называют генераторами случайных чисел (ГСЧ) или датчиками случайных чисел.

Аппаратные ГСЧ представляют собой устройства, преобразующие в цифровую форму какой-либо параметр окружающей среды или физического процесса. Параметр и процесс выбираются таким образом, чтобы обеспечить хорошую «случайность» значений при считывании. Очень часто используются паразитные процессы в электронике (токи утечки, туннельный пробой диодов, цифровой шум видеокамеры, шумы на микрофонном входе звуковой карты и т. п. ). Формируемая таким образом последовательность чисел, как правило, носит абсолютно случайный характер и не может быть воспроизведена заново по желанию пользователя.

К программным ГСЧ относятся различные алгоритмы генерирования последовательности чисел, которая по своим характеристикам напоминает случайную. Для формирования очередного числа последовательности используются различные алгебраические преобразования. Одним из первых программных ГСЧ является метод средин квадратов, предложенный в 1946 г. Дж. фон Нейманом. Этот ГСЧ формирует следующий элемент последовательности на основе предыдущего путем возведения его в квадрат и выделения средних цифр полученного числа. Например, мы хотим получить 10-значное число и предыдущее число равнялось 5772156649. Возводим его в квадрат и получаем 33317792380594909201; значит, следующим числом будет 7923805949. Очевидным недостатком этого метода является зацикливание в случае, если очередное число будет равно нулю. Кроме того, существуют и другие сравнительно короткие циклы.

Любые программные ГСЧ, не использующие внешних «источников энтропии» и формирующие очередное число только алгебраическими преобразованиями, не дают чисто случайных чисел. Последовательность на выходе такого ГСЧ выглядит как случайная, но на самом деле подчиняется некоторому закону и, как правило, рано или поздно зацикливается. Такие числа называются псевдослучайными.

В дальнейшем мы будем рассматривать лишь программные генераторы псевдослучайных чисел.

2. Характеристики ГСЧ

Последовательности случайных чисел, формируемых тем или иным ГСЧ, должны удовлетворять ряду требований. Во-первых, числа должны выбираться из определенного множества (чаще всего это действительные числа в интервале от 0 до 1 либо целые от 0 до N). Во-вторых, последовательность должна подчиняться определенному распределению на заданном множестве (чаще всего распределение равномерное). Необязательным является требование воспроизводимости последовательности. Если ГСЧ позволяет воспроизвести заново однажды сформированную последовательность, отладка программ с использованием такого ГСЧ значительно упрощается. Кроме того, требование воспроизводимости часто выдвигается при использовании ГСЧ в криптографии.

Поскольку псевдослучайные числа не являются действительно случайными, качество ГСЧ очень часто оценивается по «случайности» получаемых чисел. В эту оценку могут входить различные показатели, например, длина цикла (количество итераций, после которого ГСЧ зацикливается), взаимозависимости между соседними числами (могут выявляться с помощью различных методов теории вероятностей и математической статистики) и т. п. Подробнее оценка качества ГСЧ рассмотрена ниже.

3. Применение ГСЧ

Одна из задач, в которых применяются ГСЧ, – это грубая оценка объемов сложных областей в евклидовом пространстве более чем четырех или пяти измерений. Разумеется, сюда входит и приближенное вычисление интегралов. Обозначим область через R; обычно она определяется рядом неравенств. Предположим, что R – подмножество n‑ мерного единичного куба K. Вычисление объема множества R методом Монте-Карло сводится к тому, чтобы случайным образом выбрать в K большое число N точек, которые с одинаковой вероятностью могут оказаться в любой части K. Затем подсчитывают число M точек, попавших в R, т. е. удовлетворяющих неравенствам, определяющим R. Тогда M/N есть оценка объема R. Можно показать, что точность такой оценки будет довольно низкой. Тем не менее, выборка из 10 000 точек обеспечит точность около 1%, если только объем не слишком близок к 0 или 1. Такой точности часто бывает достаточно, и добиться лучшего другими методами может оказаться очень трудно.

В качестве примера можно рассмотреть вычисление площади фигуры, заданной некоторой системой неравенств. Пусть фигура будет определена следующим образом:

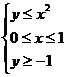Сначала необходимо определить прямоугольную область, из которой будут выбираться случайные точки. Это может быть любая область, полностью содержащая фигуру, площадь которой требуется найти. Возьмем в качестве исходной области прямоугольник с координатами углов (0; –1) – (1; 1). Будем последовательно генерировать точки, равномерно распределенные внутри этого прямоугольника, и для каждой точки проверять неравенства, описывающие фигуру. Если точка удовлетворяет всем неравенствам, значит, она принадлежит фигуре. При достаточно большом числе таких экспериментов отношение числа точек N_F, удовлетворяющих неравенствам, к общему числу сгенерированных точек N_R показывает долю площади прямоугольника, которую занимает фигура. Площадь прямоугольника S_R известна (в нашем случае она равна 2), площадь фигуры S_F вычисляется тривиально:

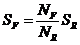Очевидно, что для такой простой области можно легко посчитать область через определенный интеграл. Тем не менее, описанный метод применим и в случае гораздо более сложных фигур, когда рассчитать площадь другим способом становится слишком сложно.

Другим примером приближенного взятия определенного интеграла с помощью ГСЧ является вычисление объема шара в n‑ мерном пространстве. Объем n‑ мерного шара выражается формулой:

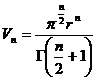где Γ (z) – некоторая гамма-функция, определяемая следующим соотношением:

Γ (z+1)=z·Γ (z),

Γ (1)=1.

Таким образом, для натуральных z гамма-функция равна факториалу z. Для вычисления знаменателя можно воспользоваться известным значением

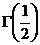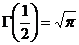Можно показать, что для шара единичного радиуса при увеличении размерности n объем стремится к нулю. Наиболее просто это можно объяснить тем, что числитель растет со скоростью степенной функции, а знаменатель – с факториальной. Таким образом, для больших n метод вычисления через случайные числа будет давать значительные погрешности.

4. Генерирование равномерно распределенных случайных чисел

Почти повсеместно используемый метод генерирования псевдослучайных целых чисел состоит в выборе некоторой функции f, отображающей множество целых чисел в себя. Выбирается какое-нибудь начальное число х₀, а каждое следующее число порождается с помощью рекуррентного соотношения:

x_k₊₁= f(x_k)

Число x_k часто называется зерном (англ. seed) ГСЧ и полностью определяет текущее состояние ГСЧ и следующее генерируемое значение.

Поначалу функции f выбирались как можно более сложные и трудно понимаемые. Например, f(x) определялась как целое число, двоичное представление которого составляет средний 31 разряд 62‑ разрядного квадрата числа x (модификация метода средин квадратов). Но отсутствие теории относительно f приводило к катастрофическим последствиям. Для метода средин квадратов это уже упоминавшееся зацикливание при обращении очередного числа в нуль. Поэтому уже довольно давно перешли к использованию функций, свойства которых вполне известны. Всякая последовательность целых чисел из интервала (0, 2³¹–1) должна содержать повторения самое большое после 2³¹≈ 10⁹ элементов. Используя теорию чисел, можно выбрать такую функцию f, для которой наперед будет известно, что ее период максимально возможный или близкий к максимальному. Этим избегается преждевременное окончание или зацикливание последовательности. Дальнейшее использование теории чисел может более или менее предсказать характер последовательности, давая пользователю некоторую степень уверенности в том, что она будет достаточно хорошо моделировать случайную последовательность чисел.

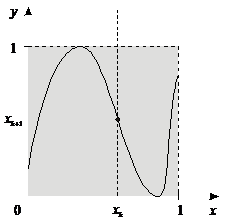
Представим генерирование чисел в диапазоне [0; 1] рекуррентым методом графически (см. рис. 1). Очевидно, функция f(x) должна быть определена на всем отрезке [0; 1] и иметь на этом отрезке непрерывную область значений [0; 1], в противном случае генерируемые числа будут составлять лишь несобственное подмножество указанного отрезка.

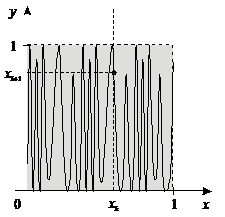
а) б)

Рис. 1. Графическое представление рекуррентного ГСЧ:

а) с «плохой» функцией f(x); б) с «хорошей» функцией f(x).

Считается, что функция f(x) тем лучше подходит для генерирования случайных чисел, чем более плотно и равномерно ее график заполняет область xÎ [0; 1], yÎ [0; 1]. Например, функция, приведенная на рис. 1, а, будет давать последовательность чисел с сильной корреляционной зависимостью соседних элементов. В случае функции, приведенная на рис. 1, б, эта зависимость будет значительно слабее.

В настоящее время широкое распространение получили линейные конгруэнтные ГСЧ. В таком ГСЧ каждое следующее число получается на основе единственного предыдущего, при этом используется функция f вида:

f(х) = (ах+с) mod m,

где для n‑ разрядных двоичных целых чисел m обычно равно 2ⁿ.

Конгруэнтный ГСЧ выдает псевдослучайные целые числа в интервале (0, m). Параметры x₀, a и c – целые числа из той же области, выбираемые исходя из следующих соображений:

1. x₀ может быть произвольно. Для проверки программы возможно x₀=1. В дальнейшем в качестве x₀ можно брать текущее время, преобразованное в число из интервала (0, m). Такой подход обеспечивает различные последовательности для различных запусков программы.

2. Выбор a должен удовлетворять трем требованиям (для двоичных машин):

a) a mod 8 = 5;

b) ;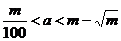

c) двоичные знаки а не должны иметь очевидного шаблона.

3. В качестве c следует выбирать нечетное число, такое, что

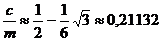Более подробные рекомендации по выбору параметров можно найти у Д. Кнута [5].

При использовании конгруэнтного ГСЧ следует помнить, что наименее значимые двоичные цифры x_k будут «не очень случайными». Поэтому, если, например, вы хотите использовать число x_k для случайного выбора одной из 16 возможных ветвей, берите наиболее значимые разряды x_k, а не наименее значимые. Наконец, для большей надежности полезно предварительно испытать случайные числа на какой-либо задаче с известным ответом, схожей с реальным приложением.

5. Генерирование чисел с произвольным распределением

Достаточно часто возникает необходимость сгенерировать последовательность случайных чисел y_i, равномерно распределенных на данном конечном интервале [a, b], с помощью ГСЧ, выдающего числа x_i на интервале [0, m]. Приведение диапазона ГСЧ к нужному интервалу в этом случае осуществляется простым линейным преобразованием:

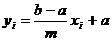Распределение чисел после такого преобразования остается равномерным.

Более сложным случаем является генерирование случайных точек из некоторого множества в n‑ мерном пространстве R ⁿ, например, точек из некоторой области на плоскости. Рассмотрим формирование случайных точек для нескольких простых областей: прямоугольника, окружности и круга.

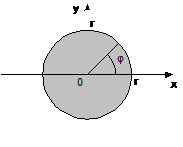
а) б) в)

Рис. 2. Области, из которых выбираются точки

Для получения равномерно распределенных случайных чисел из прямоугольника, стороны которого параллельны осям координат (см. рис. 2, а), достаточно извлекать из ГСЧ последовательно пары чисел, приводить их к нужным интервалам и использовать как координаты точки:

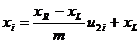
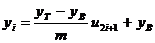где u_j – равномерно распределенное случайное число из отрезка [0, m].

Окружность можно представить одномерным множеством точек с угловой координатой φ , принимающей значения на интервале (0, 2π ). Таким образом, декартовы координаты очередной точки можно вычислить следующим образом:

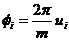
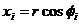
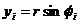где u_j – равномерно распределенное случайное число из интервала (0, m); r – радиус окружности.

В случае круга первое, что приходит в голову – воспользоваться полярной системой координат (ρ, φ ), в которой данное множество фактически представляет собой прямоугольник (а для него способ генерации чисел известен). Однако при переходе от полярных координат к декартовым нарушается распределение случайных чисел: оно становится неравномерным; плотность распределения в центре круга выше, чем по краям.

Существует несколько способов получения равномерного распределения по кругу. Рассмотрим один из них. Будем генерировать случайные пары (x, y) и для каждой из них ставить внутри круга соответствующую точку, заполняя таким образом эту область. Исходя из представлений о равномерном распределении можно предположить, что при достаточно большой длине сгенерированной последовательности на единицу площади круга будет приходиться примерно одно и то же количество точек вне зависимости от их расположения (другими словами, при равномерном распределении плотность точек по кругу будет одинакова).

Воспользуемся полярной системой координат для генерирования точек. При этом будем выбирать угол φ равномерно распределенным на интервале (0; 2π ), а распределение ρ построим следующим образом:

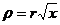где x – равномерно распределенная на отрезке [0; 1] случайная величина. Можно показать, что при таком способе формирования координат случайные точки будут равномерно распределены по всей площади круга.

Помимо выбора из произвольного множества, часто требуется формировать числа с распределением, отличным от равномерного. Распределение обычно задается функцией плотности распределения f(x) либо функцией распределения F(x). Функция распределения в произвольной точке x показывает вероятность того, что случайная величина X окажется меньше данного значения x:

F(x)=P (X< x).

Функция плотности распределения представляет собой производную F(x):

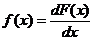Функция F(x) для любой случайной величины является неубывающей на всем интервале (–∞; +∞ ), стремится к 0 при x→ –∞ и к 1 при x→ +∞. Для получения случайных чисел с заданным распределением F(x) необходимо найти функцию, обратную к F(x), т. е. такую функцию G, что для всех y=F(x) выполняется G(y)=x. Это можно пояснить следующим образом. Предположим, что мы многократно выбираем число y, равномерно распределенное на интервале [0; 1]; каждому yмы ставим в соответствие некоторое x=G(y). Выбору 50000 игреков соответствует выбор 50000 иксов. Таким образом, доля выбранных y, лежащих между двумя фиксированными значениями, скажем y₁ и y₂, в точности равна доле x, лежащих в интервале [x₁; x₂]. Но вероятность первого из названных событий равна | y₂ – y₁ |, если y распределено равномерно; следовательно, верна цепочка равенств:

доля чисел в интервале [x₁; x₂] = доля чисел в интервале [y₁; y₂] = y₂ – y₁ = F(x₂) – F(x₁) = ,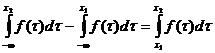

которая и показывает, что в случае равномерного распределения игреков x имеет распределение с плотностью f(τ ). Сложной проблемой в этом подходе является достаточно быстрое и точное формирование обратной функции распределения G(y).

Рассмотрим в качестве примера получение случайного числа с экспоненциальным распределением. Это распределение характеризуется одним параметром λ > 0 и имеет следующие функции распределения и плотности распределения:

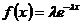, x≥ 0;

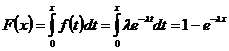Для этого распределения легко получить F^–1 (y), т. е. разрешить уравнение F(x)=y. Решение имеет вид

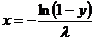Для получения x с искомым распределением нужно сгенерировать y, равномерно распределенное на (0, 1), и применить эту формулу. Если говорить о практической стороне дела, то существуют более эффективные способы, в которых не используется медленная операция вычисления логарифма для каждого случайного числа. Данный способ продемонстрирован лишь как пример более общего подхода с использованием обратной функции распределения.

6. Тестирование ГСЧ

Качество ГСЧ в значительной мере влияет на результаты работы программ, использующих случайные числа. Поэтому все применяемые генераторы случайных чисел должны пройти перед моделированием системы предварительное тестирование, которое представляет собой комплекс проверок по различным стохастическим критериям, включая в качестве основных тесты на равномерность, стохастичность и независимость (рассматриваются только ГСЧ с равномерным распределением).

Проверка равномерности последовательностей псевдослучайных равномерно распределенных чисел {x_i} может быть выполнена по гистограмме с присваиванием косвенных признаков. Суть проверки по гистограмме сводится к следующему. Выдвигается гипотеза о равномерности распределения чисел (0, 1). Затем интервал (0, 1) разбивается на m равных частей, тогда при генерации последовательности {x_i} каждое из чисел x_i c вероятностью 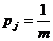, , 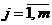попадет в один из подынтервалов. Всего в каждый j‑ й подынтервал попадает N_i чисел последовательности {x_i}, 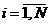, причём 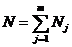. Относительная частота попадания случайных чисел из последовательности {x_i} в каждый из подынтервалов будет равна N_j/N. Очевидно, что если числа x_i принадлежат псевдослучайной квазиравномерно распределенной последовательности, то при достаточно больших N экспериментальная гистограмма (ломаная линия на рис. 3, а) приближается к теоретической прямой 1/m. Оценка степени приближения, т. е. равномерности последовательности {x_i}, может быть проведена с использованием критериев согласия.

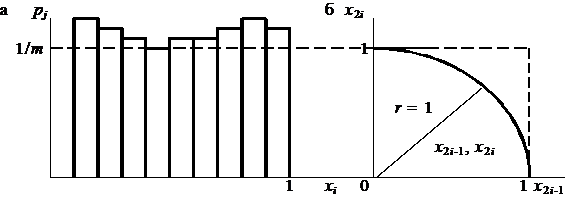
Рис. 3. Проверка равномерности последовательности

Существуют и другие способы проверки равномерности распределения.

Проверка стохастичности последовательности псевдослучайных чисел {x_i} наиболее часто проводится методами комбинаций и серий. Сущность метода сводится к определению закона распределения длин участков между единицами (нулями) или закона распределения (появления) числа единиц (нулей) в n-разрядном двоичном числе X_i.

Теоретически закон появления j единиц в l разрядах двоичного числа X_i описывается, исходя из независимости отдельных разрядов, биномиальным законом распределения:

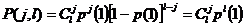где P (j, l) – вероятность появления j единиц в l разрядах числа X_i;

p(1) = p(0) = 0, 5 – вероятность появления единицы и нуля в любом разряде числа X_i;

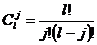Тогда при фиксированной точке выборки N теоретически ожидаемое число появления случайных чисел X_i с j единицами в проверяемых l разрядах будет равно .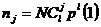

После нахождения теоретических и экспериментальных вероятностей P (j, l) или чисел n_j при различных значениях l £ n гипотеза о стохастичности проверяется с использованием критериев согласия, которые подробно рассматриваются в курсе математической статистики.

При анализе стохастичности последовательности чисел {x_i} методом серий последовательность разбивается на элементы первого и второго рода (a и b), т. е.

где 0 < p < 1.

Серией называется отрезок последовательности {x_i}, состоящий из идущих друг за другом элементов одного и того же рода. Число элементов в отрезке (a или b) называется длиной серии.

После разбиения последовательности {x_i} на серии первого и второго рода будем иметь, например, серию вида

….. aabbbbaaabbbaabbab….

Так как случайные числа a и b в данной последовательности независимы и принадлежат последовательности {x_i}, равномерно распределённой на интервале (0, 1), то теоретическая вероятность появления серии длиной j в N опытах (под опытом здесь понимается генерация числа x_i и проверка условия x_i < p) определится формулой Бернулли:

, , .

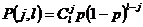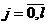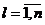В случае экспериментальной проверки оцениваются частоты появления серий длиной j. В результате получаются экспериментальная и теоретическая зависимости P (j, l), сходимость которых проверяется по известным критериям, причем проверку целесообразно проводить при разных значениях l и р, 0 < р < 1.

Библиографический список

1. Форсайт Дж. Машинные методы математических вычислений / Дж. Форсайт, М. Малькольм, К. Моулер. М.: Мир, 1980. – 279 с.

2. Кнут Д. Искусство программирования, том 2. Получисленные методы / Д. Кнут. М.: Изд. дом «Вильямс», 2007. 832 с.

3. Каханер Д. Численные методы и математическое обеспечение: Пер. с англ. / Д. Каханер, К. Моулер, С. Нэш. М.: Мир, 1998. – 575 с., ил.

4. Зубинский А. В поисках случайности // А. Зубинский. Компьютерное обозрение №29, 2003.