
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Коллоквиум сұрақтары 2 страница
44. 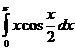 =
=
A) 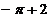 ; B)
; B) 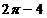 ; C)
; C) 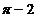 ; D)
; D) 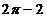 ; E)
; E) 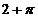 .
.
45. 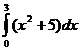 =
=
A) 15; B) 12; C) 8; D) 24; E) 56.
46. Егер 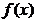 функциясы
функциясы 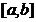 кесіндісінде ү зіліссіз болса, онда табылады
кесіндісінде ү зіліссіз болса, онда табылады 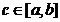 нү ктесі, келесі тең дік орындалатындай
нү ктесі, келесі тең дік орындалатындай
A) 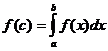 ; B)
; B) 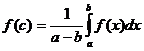 ; C)
; C) 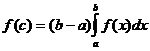 ;
;
D) 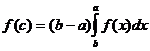 ; E)
; E) 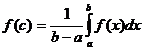 .
.
47. Анық талғ ан интегралдың бө ліктеп интегралдау формуласы?
A) 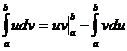 ; B)
; B) 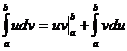 ; C)
; C) 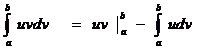 ;
;
D) 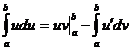 ; E)
; E) 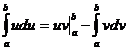 .
.
48. 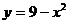 жә не
жә не  сызық тарымен шектелген фигураның ауданын табу?
сызық тарымен шектелген фигураның ауданын табу?
A)  ; B) 36; C) 5; D)
; B) 36; C) 5; D) 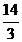 ; E) 2.
; E) 2.
49. 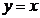 ,
, 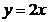 ,
, 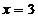 сызық тарымен шектелген фигураның ауданын табу?
сызық тарымен шектелген фигураның ауданын табу?
A) 7; B) 5; C) 1, 5; D) 4, 5; E) 6.
50. 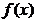 жә не
жә не 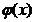 ү зіліссіз функциялар
ү зіліссіз функциялар 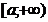 аралығ ында
аралығ ында 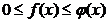 қ асиетіне ие болса, онда
қ асиетіне ие болса, онда
F) 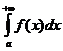 интегралының жинақ талуынан
интегралының жинақ талуынан 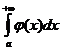 интегралы жинақ талады;
интегралы жинақ талады;
G) 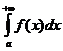 қ атарының жинақ талмауынан
қ атарының жинақ талмауынан 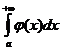 қ атарының жинақ талмайтыны шығ ады;
қ атарының жинақ талмайтыны шығ ады;
H) 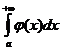 қ атарының жинақ талмауынан
қ атарының жинақ талмауынан 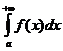 қ атарының жинақ талмайтыны шығ ады;
қ атарының жинақ талмайтыны шығ ады;
I) 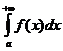 жә не
жә не 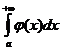 интегралдары біруақ ытта жинақ талады;
интегралдары біруақ ытта жинақ талады;
J) 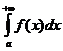 жә не
жә не 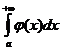 интегралдары біруақ ытта жинақ талмайды
интегралдары біруақ ытта жинақ талмайды
51. Жалпыланғ ан гармоникалық қ атар 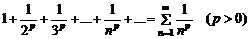 жинақ талады, егер
жинақ талады, егер
A) 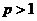 B)
B) 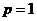 C)
C) 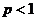 D)
D) 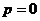 E)
E) 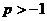
52. 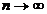 ұ мтылғ анда
ұ мтылғ анда 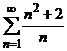 қ атарының жалпы мү шесінің шегі неге тең:
қ атарының жалпы мү шесінің шегі неге тең:
A) 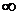 B) 1 C)
B) 1 C) 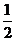 D) 2 E) 0
D) 2 E) 0
53. 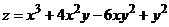 .
. 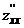 неге тең?
неге тең?
A)  B)
B)  C)
C) 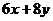 D)
D) 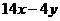 E)
E) 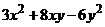
54. 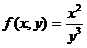 ,
, 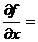
A) 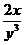 ; B)
; B) 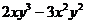 ; C)
; C) 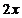 ; D)
; D) 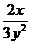 ; E)
; E) 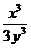 .
.
55. 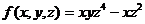 ,
, 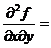
A) 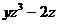 ; B)
; B) 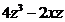 ; C)
; C) 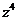 ; D)
; D)  ; E)
; E) 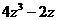 .
.
56. 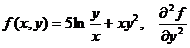 =
=
A) 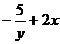 ; B)
; B) 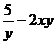 C)
C) 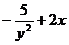 D)
D) 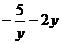 E)
E) 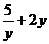
57. Коши есебінің шешімін табың дар 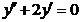 ,
, 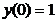 ,
, 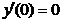
A) 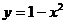 ; B)
; B) 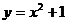 ; C)
; C) 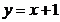 ; D)
; D) 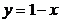 ; E)
; E) 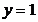 .
.
58. 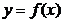 тең деуімен берілген AB қ исық доғ аның ұ зындығ ы қ андай формуламен есептелінеді l=?
тең деуімен берілген AB қ исық доғ аның ұ зындығ ы қ андай формуламен есептелінеді l=?
A)  , B)
, B) 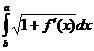 , C)
, C) 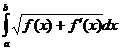 , D)
, D) 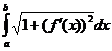 , E)
, E) 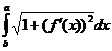 .
.
59. Егер 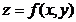 дифференциалданатын функцияның
дифференциалданатын функцияның 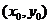 нү ктесінде экстремумы бар болса, онда
нү ктесінде экстремумы бар болса, онда
A) 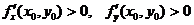 ; B)
; B) 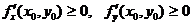 ; C)
; C) 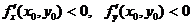 ;
;
D) 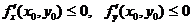 ; E)
; E) 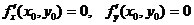 .
.
60. 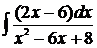 =
=
A) 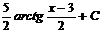 B)
B) 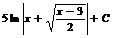 C)
C) 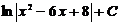
D) 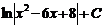 E)
E) 
61. (Қ атар жинақ талуының қ ажетті белгісі) Егер 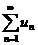 қ атары жинақ талса, онда
қ атары жинақ талса, онда
A) 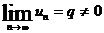 ; B)
; B) 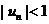 ; C)
; C)  ; D)
; D) 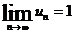 ; E)
; E) 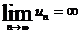 .
.
62. 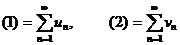 ─ ─ таң балары оң қ атарлар болсын. Сонымен
─ ─ таң балары оң қ атарлар болсын. Сонымен  . Онда
. Онда
A) (2) қ атардың жинақ талмауынан (1) қ атардың жинақ талмайтыны шығ ады;
B) (1) қ атардың жинақ талуынан (2) қ атардың жинақ талуы шығ ады;
C) (2) қ атардың жинақ талуынан (1) қ атардың жинақ талуы шығ ады;
D) екі қ атар бір уақ ытта жинақ талады;
E) екі қ атар бір уақ ытта жинақ талмайды.
63. Сандық қ атардың Даламбер белгісі:
A)  , егер q< 1 қ атар жинақ ты, егер q> 1 қ атар жинақ сыз;
, егер q< 1 қ атар жинақ ты, егер q> 1 қ атар жинақ сыз;
B) 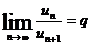 , егер q> 1 қ атар жинақ ты, егер q< 1 қ атар жинақ сыз;
, егер q> 1 қ атар жинақ ты, егер q< 1 қ атар жинақ сыз;
C) 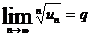 , егер q< 1 қ атар жинақ ты, егер q> 1 қ атар жинақ сыз;
, егер q< 1 қ атар жинақ ты, егер q> 1 қ атар жинақ сыз;
D) 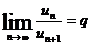 , егер q< 1 қ атар жинақ ты, егер q> 1 қ атар жинақ сыз;
, егер q< 1 қ атар жинақ ты, егер q> 1 қ атар жинақ сыз;
E) 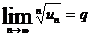 , егер q> 1 қ атар жинақ ты, егер q< 1 қ атар жинақ сыз.
, егер q> 1 қ атар жинақ ты, егер q< 1 қ атар жинақ сыз.
64. Жинақ талмайтын қ атарды кө рсет?
A) 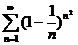 ; B)
; B) 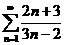 ; C)
; C) 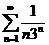 ; D)
; D) 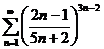 ; E)
; E) 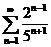 .
.
65. Дифференциалдық тең деудің жеке шешімін тап  ;
; 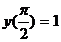 .
.
A) 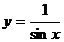 ; B)
; B) 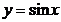 ; C)
; C) 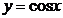 ; D)
; D) 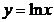 ; E)
; E) 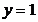 .
.
66. 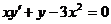 тең деудің жалпы шешімін тап?
тең деудің жалпы шешімін тап?
A) 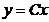 ; B)
; B) 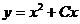 ; C)
; C) 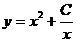 ; D)
; D) 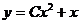 ; E)
; E) 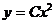 .
.
67. 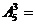
A) 10 B) 15 C) 30 D) 60 E) 45
68. 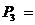
A) 3 B) 9 C) 6 D) 27 E) 12
69. 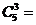
A) 15 B) 10 C) 60 D) 45 E) 30
70. Анық тама. 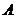 оқ иғ асына қ олайлы элементар оқ иғ алар санының сынаудың тең мү мкіндікті барлық элементар оқ иғ алар санына қ атынасын
оқ иғ асына қ олайлы элементар оқ иғ алар санының сынаудың тең мү мкіндікті барлық элементар оқ иғ алар санына қ атынасын 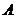 оқ иғ асының ық тималдығ ы деп атайды.
оқ иғ асының ық тималдығ ы деп атайды.
A) ық тималдық тың геометриялық анық тамасы
B) ық тималдық тың классикалық анық тамасы
C) ық тималдық тың аксиоматикалық анық тамасы
D) ық тималдық тың статистикалық анық тамасы
Е) оқ иғ аның анық тамасы.
{Дұ рыс жауабы} = В
71. Жә шікте 3 ақ, 2 қ ара жә не 5 қ ызыл шар бар. Жә шіктен кездейсоқ алынғ ан шардың қ ара емес болу ық тималдығ ы неге тең
A) 0, 3
B) 0, 8
C) 0, 2
D) 0, 6
Е) 0
72. А, В- ү йлесімсіз оқ иғ алары ү шін мына тең дік орындалады
A) P(A-B)=P(A)-P(B) B) P(A+B)=P(A)+P(B)- P(A·В)
C) P(A+B)=P(A)+P(B)+ P(A·В) D) P(A+B)=P(A)·P(B) Е) P(A+B)=P(A)+P(B)
73. 1-ден 30-ғ а дейінгі бү тін сандардан кездейсоқ бір сан алынғ ан. Сол алынғ ан санның 5-ке бө лінуінің ық тималдығ ы
A) 0, 3 B) 0, 4 C) 0 D) 0, 2 Е) 0
74. Берілген кездейсоқ шамалардың ү лестіру заң ына сә йкес қ алып кеткен мә нді тап?
| x | -1 | |||
| p | 0, 1 | 0, 3 | 0, 1 | ? |
A) 0, 5 B) 0, 2 C) 0, 1 D) 0, 3 E) 0, 4
75. Берілген кездейсоқ шамалардың ү лестіру заң ына сә йкес 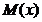 математикалық кү тімін тап?
математикалық кү тімін тап?
| x | -1 | ||
| p | 0, 3 | 0, 3 | 0, 4 |
A) 0 B) 1, 8 C) 1 D) 1, 2 E) 2, 8
76. X жә не Y кездейсоқ шамалары– тә уелсіз, сонымен 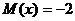 ,
, 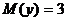 . Онда
. Онда 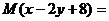
A) 8 B) -8 C) 0 D) 16 E) 14
77. X жә не Y кездейсоқ шамалары– тә уелсіз, сонымен 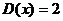 ,
, 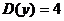 . Онда
. Онда 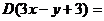
A) 5 B) 22 C) 123 D) 25 E) 17
78. Екінші ретті дифференциалдық тең деудің жалпы шешімін тап 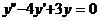
A) 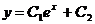 B)
B) 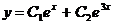 C)
C) 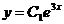
D) 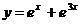 E) дұ рыс жауабы жоқ
E) дұ рыс жауабы жоқ
79. ОY осін айналатын қ исық сызық ты трапецияның айналу кө лемінің формуласы
A) 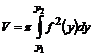 B)
B) 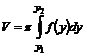 C)
C) 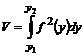
D) 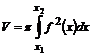 E)
E) 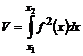
80. Дә режелік қ атар ү шін абсолютті жинақ талу радиусы қ ай формула бойынша есептелінеді?
A) 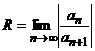 B)
B) 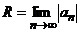 C)
C) 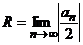
D) 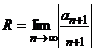 E)
E) 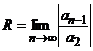
81. 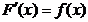 болсын. Онда
болсын. Онда 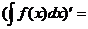
A) 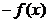 ; B)
; B) 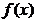 ; C)
; C) 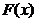 ; D) ─
; D) ─ 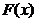 E) 0.
E) 0.
82. 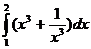 =
=
A) -1, 25; B) 3, 875; C) 2, 125; D) -2, 125; E) 4, 125.
83. 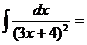
A) 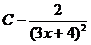 ; B)
; B)  ; C)
; C) 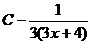 ; D)
; D) 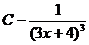 ; E)
; E) 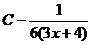 .
.
84. 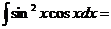
A)  ; B)
; B) 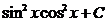 ; C)
; C) 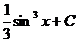 ; D)
; D) 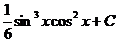 ; E)
; E) 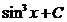 .
.
85. 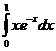 =
=
A) 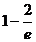 ; B)
; B) 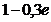 ; C)
; C) 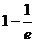 ; D)
; D) 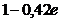 ; E)
; E)  .
.
86. Екінші ретті дифференциалдық тең деудің жалпы шешімін тап 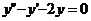
A) 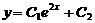 ; B)
; B) 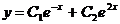 ; C)
; C) 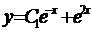 ;
;
D)  ; E) дұ рыс жауабы жоқ.
; E) дұ рыс жауабы жоқ.
87. Екінші ретті дифференциалдық тең деудің жалпы шешімін тап 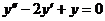
A) 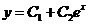 ; B)
; B)  ; C)
; C) 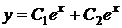 ;
;
D) 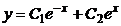 ; E)
; E) 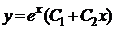 .
.
88. 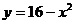 жә не
жә не  сызық тарымен шектелген фигураның ауданын есепте
сызық тарымен шектелген фигураның ауданын есепте
A) 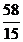 ; B)
; B) 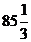 ; C)
; C) 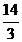 ; D) 5; E)
; D) 5; E) 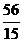 .
.
89. 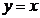 ,
, 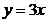 ,
, 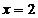 сызық тарымен шектелген фигураның ауданын есепте
сызық тарымен шектелген фигураның ауданын есепте
A) 2; B) 5; C) 1; D) 4; E) 6.
90. 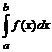 геометриялық мағ ынасы?
геометриялық мағ ынасы?
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|