| Анализ временных рядов
| Time Series Analysis
|
| • Общее введение
| |
| • Две основные цели
| |
| • Идентификация модели временных рядов
| - Identifying Patterns in Time Series Data
|
| o Систематическая составляющая и случайный шум
| - Systematic pattern and random noise
|
| o Два общих типа компонент временных рядов
| - Two general aspects of time series patterns
|
| o Анализ тренда
| |
| o Анализ сезонности
| |
| • АРПСС (Бокс и Дженкинс) и автокорреляции
| - ARIMA (Box & Jenkins) and Autocorrelations
|
| o Общее введение
| |
| o Два основных процесса
| |
| o Модель АРПСС
| o ARIMA Methodology
|
| o Идентификация
| |
| o Оценивание параметров
| |
| o Оценивание модели
| |
| • Прерванные временные ряды
| |
| • Экспоненциальное сглаживание
| |
| o Общее введение
| |
| o Простое экспоненциальное сглаживание
| - Simple Exponential Smoothing
|
| o Выбор лучшего значения параметра a (альфа)
| - Choosing the Best Value for Parameter a (alpha)
|
| o Индексы качества подгонки
| - Indices of Lack of Fit (Error)
|
| o Сезонная и несезонная модели с трендом или без тренда
| - Seasonal and Non-seasonal Models With or Without Trend
|
| • Сезонная декомпозиция (метод Census I)
| - Seasonal Decomposition (Census I)
|
| o Общее введение
| |
| o Вычисления
| |
| • Сезонная корректировка X-11 (метод Census II)
| - X-11 Census method II seasonal adjustment
|
| o Сезонная корректировка: основные идеи и термины
| - Seasonal Adjustment: Basic Ideas and Terms
|
| o Метод Census II
| |
| o Таблицы результатов корректировки X-11
| - Results Tables Computed by the X-11 Method
|
| o Подробное описание всех таблиц результатов, вычисляемых в методе X-11
| - Specific Description of all Results Tables Computed by the X-11 Method
|
| • Анализ распределенных лагов
| - Distributed Lags Analysis
|
| o Общая цель
| |
| o Общая модель
| |
| o Распределенный лаг Алмона
| |
| • Одномерный анализ Фурье
| - Single Spectrum (Fourier) Analysis
|
| • Кросс-спектральный анализ
| |
| o Общее введение
| |
| o Основные понятия и принципы
| - Basic Notation and Principles
|
| o Результаты для каждой переменной
| - Results for Each Variable
|
| o Кросс-периодограмма, кросс-плотность, квадратурная плотность и кросс-амплитуда
| - The Cross-periodogram, Cross-density, Quadrature-density, and Cross-amplitude
|
| o Квадрат когерентности, усиление и фазовый сдвиг
| - Squared Coherency, Gain, and Phase Shift
|
| o Как создавались данные для примера
| - How the Example Data were Created
|
| • Спектральный анализ - Основные понятия и принципы
| - Spectrum Analysis - Basic Notations and Principles
|
| o Частота и период
| |
| o Общая структура модели
| - The General Structural Model
|
| o Простой пример
| |
| o Периодограмма
| |
| o Проблема рассеяния
| |
| o Добавление констант во временной ряд (пэддинг)
| |
| o Косинус-сглаживание
| |
| o Окна данных и оценки спектральной плотности
| - Data Windows and Spectral Density Estimates
|
| o Подготовка данных к анализу
| - Preparing the Data for Analysis
|
| o Результаты для случая, когда в ряде отсутствует периодичность
| - Results when no Periodicity in the Series Exists
|
| • Быстрое преобразование Фурье
| - Fast Fourier Transformations
|
| o Общее введение
| |
| o Вычисление БПФ во временных рядах
| - Computation of FFT in Time Series
|
| В следующих разделах мы вначале представим обзор методов, используемых для идентификации моделей временных рядов (таких как сглаживание, подгонка и автокорреляции). Затем опишем общий класс моделей, которые могут быть использованы для описания рядов и построения прогнозов (модели авторегрессии и скользящего среднего). Наконец, расскажем о некоторых простых, но часто используемых методах, основанных на линейной регрессии. За дальнейшей информацией обратитесь к соответствующим разделам.
|
|
|
| In the following topics, we will first review techniques used to identify patterns in time series data (such as smoothing and curve fitting techniques and autocorrelations), then we will introduce a general class of models that can be used to represent time series data and generate predictions (autoregressive and moving average models). Finally, we will review some simple but commonly used modeling and forecasting techniques based on linear regression. For more information on these topics, see the topic name below.
|
| Общее введение
| General Introduction
|
| Вначале дадим краткий обзор методов анализа данных, представленных в виде временных рядов, т. е. в виде последовательностей измерений, упорядоченных в неслучайные моменты времени. В отличие от анализа случайных выборок, анализ временных рядов основывается на предположении, что последовательные значения в файле данных наблюдаются через равные промежутки времени (тогда как в других методах нам не важна и часто не интересна привязка наблюдений ко времени).
| In the following topics, we will review techniques that are useful for analyzing time series data, that is, sequences of measurements that follow non-random orders. Unlike the analyses of random samples of observations that are discussed in the context of most other statistics, the analysis of time series is based on the assumption that successive values in the data file represent consecutive measurements taken at equally spaced time intervals.
|
| Подробное обсуждение этих методов можно найти в следующих работах: Anderson (1976), Бокс и Дженкинс (1976), Kendall (1984), Kendall and Ord (1990), Montgomery, Johnson, and Gardiner (1990), Pankratz (1983), Shumway (1988), Vandaele (1983), Walker (1991), Wei (1989).
| Detailed discussions of the methods described in this section can be found in Anderson (1976), Box and Jenkins (1976), Kendall (1984), Kendall and Ord (1990), Montgomery, Johnson, and Gardiner (1990), Pankratz (1983), Shumway (1988), Vandaele (1983), Walker (1991), and Wei (1989).
|
|
|
|
| Две основные цели
| Two Main Goals
|
| Существуют две основные цели анализа временных рядов: (1) определение природы ряда и (2) прогнозирование (предсказание будущих значений временного ряда по настоящим и прошлым значениям). Обе эти цели требуют, чтобы модель ряда была идентифицирована и, более или менее, формально описана. Как только модель определена, вы можете с ее помощью интерпретировать рассматриваемые данные (например, использовать в вашей теории для понимания сезонного изменения цен на товары, если занимаетесь экономикой). Не обращая внимания на глубину понимания и справедливость теории, вы можете экстраполировать затем ряд на основе найденной модели, т. е. предсказать его будущие значения.
| There are two main goals of time series analysis: (a) identifying the nature of the phenomenon represented by the sequence of observations, and (b) forecasting (predicting future values of the time series variable). Both of these goals require that the pattern of observed time series data is identified and more or less formally described. Once the pattern is established, we can interpret and integrate it with other data (i. e., use it in our theory of the investigated phenomenon, e. g., sesonal commodity prices). Regardless of the depth of our understanding and the validity of our interpretation (theory) of the phenomenon, we can extrapolate the identified pattern to predict future events.
|
| Идентификация модели временных рядов
| Identifying Patterns in Time Series Data
|
| • Систематическая составляющая и случайный шум
| Systematic pattern and random noise
|
| • Два общих типа компонент временных рядов
| - Two general aspects of time series patterns
|
| • Анализ тренда
| |
| • Анализ сезонности
| |
| За более полной информацией о простых автокорреляциях (обсуждаемых в этом разделе) и других автокорреляциях, см. Anderson (1976), Box and Jenkins (1976), Kendall (1984), Pankratz (1983), and Vandaele (1983). См. также:
| - For more information on simple autocorrelations (introduced in this section) and other auto correlations, see Anderson (1976), Box and Jenkins (1976), Kendall (1984), Pankratz (1983), and Vandaele (1983). See also:
|
| • АРПСС (Бокс и Дженкинс) и автокорреляции
| ARIMA (Box & Jenkins) and Autocorrelations
|
| • Прерванные временные ряды
| |
| • Экспоненциальное сглаживание
| |
| • Сезонная декомпозиция (метод Census I)
| - Seasonal Decomposition (Census I)
|
| • Сезонная корректировка X-11 (метод Census II)
| - X-11 Census method II seasonal adjustment
|
| • Таблицы результатов корректировки X-11
| - X-11 Census method II result tables
|
| • Анализ распределенных лагов
| - Distributed Lags Analysis
|
| • Одномерный анализ Фурье
| - Single Spectrum (Fourier) Analysis
|
| • Кросс-спектральный анализ
| |
| • Основные понятия и принципы
| - Basic Notations and Principles
|
| • Быстрое преобразование Фурье
| - Fast Fourier Transformations
|
| Систематическая составляющая и случайный шум
| - Systematic Pattern and Random Noise
|
| Как и большинство других видов анализа, анализ временных рядов предполагает, что данные содержат систематическую составляющую (обычно включающую несколько компонент) и случайный шум (ошибку), который затрудняет обнаружение регулярных компонент. Большинство методов исследования временных рядов включает различные способы фильтрации шума, позволяющие увидеть регулярную составляющую более отчетливо.
| As in most other analyses, in time series analysis it is assumed that the data consist of a systematic pattern (usually a set of identifiable components) and random noise (error) which usually makes the pattern difficult to identify. Most time series analysis techniques involve some form of filtering out noise in order to make the pattern more salient.
|
| Два общих типа компонент временных рядов
| Two General Aspects of Time Series Patterns
|
| Большинство регулярных составляющих временных рядов принадлежит к двум классам: они являются либо трендом, либо сезонной составляющей. Тренд представляет собой общую систематическую линейную или нелинейную компоненту, которая может изменяться во времени. Сезонная составляющая - это периодически повторяющаяся компонента. Оба эти вида регулярных компонент часто присутствуют в ряде одновременно. Например, продажи компании могут возрастать из года в год, но они также содержат сезонную составляющую (как правило, 25% годовых продаж приходится на декабрь и только 4% на август).
| Most time series patterns can be described in terms of two basic classes of components: trend and seasonality. The former represents a general systematic linear or (most often) nonlinear component that changes over time and does not repeat or at least does not repeat within the time range captured by our data (e. g., a plateau followed by a period of exponential growth). The latter may have a formally similar nature (e. g., a plateau followed by a period of exponential growth), however, it repeats itself in systematic intervals over time. Those two general classes of time series components may coexist in real-life data. For example, sales of a company can rapidly grow over years but they still follow consistent seasonal patterns (e. g., as much as 25% of yearly sales each year are made in December, whereas only 4% in August).
|
| 
|
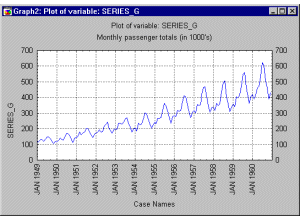
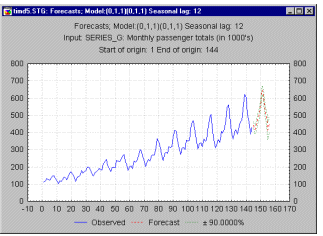
| Эту общую модель можно понять на " классическом" ряде - Ряд G (Бокс и Дженкинс, 1976, стр. 531), представляющем месячные международные авиаперевозки (в тысячах) в течение 12 лет с 1949 по 1960 (см. файл Series_g. sta). График месячных перевозок ясно показывает почти линейный тренд, т. е. имеется устойчивый рост перевозок из года в год (примерно в 4 раза больше пассажиров перевезено в 1960 году, чем в 1949). В то же время характер месячных перевозок повторяется, они имеют почти один и тот же характер в каждом годовом периоде (например, перевозок больше в отпускные периоды, чем в другие месяцы). Этот пример показывает довольно определенный тип модели временного ряда, в которой амплитуда сезонных изменений увеличивается вместе с трендом. Такого рода модели называются моделями с мультипликативной сезонностью.
| This general pattern is well illustrated in a " classic" Series G data set (Box and Jenkins, 1976, p. 531) representing monthly international airline passenger totals (measured in thousands) in twelve consecutive years from 1949 to 1960 (see example data file G. sta and graph above). If you plot the successive observations (months) of airline passenger totals, a clear, almost linear trend emerges, indicating that the airline industry enjoyed a steady growth over the years (approximately 4 times more passengers traveled in 1960 than in 1949). At the same time, the monthly figures will follow an almost identical pattern each year (e. g., more people travel during holidays then during any other time of the year). This example data file also illustrates a very common general type of pattern in time series data, where the amplitude of the seasonal changes increases with the overall trend (i. e., the variance is correlated with the mean over the segments of the series). This pattern which is called multiplicative seasonality indicates that the relative amplitude of seasonal changes is constant over time, thus it is related to the trend.
|
| Анализ тренда
| Trend Analysis
|
| Не существует " автоматического" способа обнаружения тренда в временном ряде. Однако если тренд является монотонным (устойчиво возрастает или устойчиво убывает), то анализировать такой ряд обычно нетрудно. Если временные ряды содержат значительную ошибку, то первым шагом выделения тренда является сглаживание.
| There are no proven " automatic" techniques to identify trend components in the time series data; however, as long as the trend is monotonous (consistently increasing or decreasing) that part of data analysis is typically not very difficult. If the time series data contain considerable error, then the first step in the process of trend identification is smoothing.
|
| Сглаживание. Сглаживание всегда включает некоторый способ локального усреднения данных, при котором несистематические компоненты взаимно погашают друг друга. Самый общий метод сглаживания - скользящее среднее, в котором каждый член ряда заменяется простым или взвешенным средним n соседних членов, где n - ширина " окна" (см. Бокс и Дженкинс, 1976; Velleman and Hoaglin, 1981). Вместо среднего можно использовать медиану значений, попавших в окно. Основное преимущество медианного сглаживания, в сравнении со сглаживанием скользящим средним, состоит в том, что результаты становятся более устойчивыми к выбросам (имеющимся внутри окна). Таким образом, если в данных имеются выбросы (связанные, например, с ошибками измерений), то сглаживание медианой обычно приводит к более гладким или, по крайней мере, более " надежным" кривым, по сравнению со скользящим средним с тем же самым окном. Основной недостаток медианного сглаживания в том, что при отсутствии явных выбросов, он приводит к более " зубчатым" кривым (чем сглаживание скользящим средним) и не позволяет использовать веса.
| Smoothing. Smoothing always involves some form of local averaging of data such that the nonsystematic components of individual observations cancel each other out. The most common technique is moving average smoothing which replaces each element of the series by either the simple or weighted average of n surrounding elements, where n is the width of the smoothing " window" (see Box & Jenkins, 1976; Velleman & Hoaglin, 1981). Medians can be used instead of means. The main advantage of median as compared to moving average smoothing is that its results are less biased by outliers (within the smoothing window). Thus, if there are outliers in the data (e. g., due to measurement errors), median smoothing typically produces smoother or at least more " reliable" curves than moving average based on the same window width. The main disadvantage of median smoothing is that in the absence of clear outliers it may produce more " jagged" curves than moving average and it does not allow for weighting.
|
| Относительно реже, когда ошибка измерения очень большая, используется метод сглаживания методом наименьших квадратов, взвешенных относительно расстояния или метод отрицательного экспоненциально взвешенного сглаживания. Все эти методы отфильтровывают шум и преобразуют данные в относительно гладкую кривую (см. соответствующие разделы, где каждый из этих методов описан более подробно). Ряды с относительно небольшим количеством наблюдений и систематическим расположением точек могут быть сглажены с помощью бикубических сплайнов.
| In the relatively less common cases (in time series data), when the measurement error is very large, the distance weighted least squares smoothing or negative exponentially weighted smoothing techniques can be used. All those methods will filter out the noise and convert the data into a smooth curve that is relatively unbiased by outliers (see the respective sections on each of those methods for more details). Series with relatively few and systematically distributed points can be smoothed with bicubic splines.
|
| Подгонка функции. Многие монотонные временные ряды можно хорошо приблизить линейной функцией. Если же имеется явная монотонная нелинейная компонента, то данные вначале следует преобразовать, чтобы устранить нелинейность. Обычно для этого используют логарифмическое, экспоненциальное или (менее часто) полиномиальное преобразование данных.
| Fitting a function. Many monotonous time series data can be adequately approximated by a linear function; if there is a clear monotonous nonlinear component, the data first need to be transformed to remove the nonlinearity. Usually a logarithmic, exponential, or (less often) polynomial function can be used.
|
| Анализ сезонности
| Analysis of Seasonality
|
| Периодическая и сезонная зависимость (сезонность) представляет собой другой общий тип компонент временного ряда. Это понятие было проиллюстрировано ранее на примере авиаперевозок пассажиров. Можно легко видеть, что каждое наблюдение очень похоже на соседнее; дополнительно, имеется повторяющаяся сезонная составляющая, это означает, что каждое наблюдение также похоже на наблюдение, имевшееся в том же самом месяце год назад. В общем, периодическая зависимость может быть формально определена как корреляционная зависимость порядка k между каждым i-м элементом ряда и (i-k)-м элементом (Kendall, 1976). Ее можно измерить с помощью автокорреляции (т. е. корреляции между самими членами ряда); k обычно называют лагом (иногда используют эквивалентные термины: сдвиг, запаздывание). Если ошибка измерения не слишком большая, то сезонность можно определить визуально, рассматривая поведение членов ряда через каждые k временных единиц.
| Seasonal dependency (seasonality) is another general component of the time series pattern. The concept was illustrated in the example of the airline passengers data above. It is formally defined as correlational dependency of order k between each i'th element of the series and the (i-k)'th element (Kendall, 1976) and measured by autocorrelation (i. e., a correlation between the two terms); k is usually called the lag. If the measurement error is not too large, seasonality can be visually identified in the series as a pattern that repeats every k elements.
|
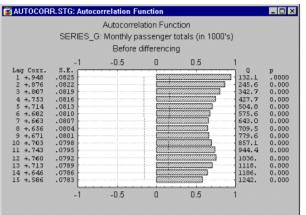
| Автокорреляционная коррелограмма. Сезонные составляющие временного ряда могут быть найдены с помощью коррелограммы. Коррелограмма (автокоррелограмма) показывает численно и графически автокорреляционную функцию (AКФ), иными словами коэффициенты автокорреляции (и их стандартные ошибки) для последовательности лагов из определенного диапазона (например, от 1 до 30). На коррелограмме обычно отмечается диапазон в размере двух стандартных ошибок на каждом лаге, однако обычно величина автокорреляции более интересна, чем ее надежность, потому что интерес в основном представляют очень сильные (а, следовательно, высоко значимые) автокорреляции (см. Элементарные понятия статистики).
| Autocorrelation correlogram. Seasonal patterns of time series can be examined via correlograms. The correlogram (autocorrelogram) displays graphically and numerically the autocorrelation function (ACF), that is, serial correlation coefficients (and their standard errors) for consecutive lags in a specified range of lags (e. g., 1 through 30). Ranges of two standard errors for each lag are usually marked in correlograms but typically the size of auto correlation is of more interest than its reliability (see Elementary Concepts) because we are usually interested only in very strong (and thus highly significant) autocorrelations.
|
| Исследование коррелограмм. При изучении коррелограмм следует помнить, что автокорреляции последовательных лагов формально зависимы между собой. Рассмотрим следующий пример. Если первый член ряда тесно связан со вторым, а второй с третьим, то первый элемент должен также каким-то образом зависеть от третьего и т. д. Это приводит к тому, что периодическая зависимость может существенно измениться после удаления автокорреляций первого порядка, т. е. после взятия разности с лагом 1).
| Examining correlograms. While examining correlograms one should keep in mind that autocorrelations for consecutive lags are formally dependent. Consider the following example. If the first element is closely related to the second, and the second to the third, then the first element must also be somewhat related to the third one, etc. This implies that the pattern of serial dependencies can change considerably after removing the first order auto correlation (i. e., after differencing the series with a lag of 1).
|
| 
|
| 
|
| Частные автокорреляции. Другой полезный метод исследования периодичности состоит в исследовании частной автокорреляционной функции (ЧАКФ), представляющей собой углубление понятия обычной автокорреляционной функции. В ЧАКФ устраняется зависимость между промежуточными наблюдениями (наблюдениями внутри лага). Другими словами, частная автокорреляция на данном лаге аналогична обычной автокорреляции, за исключением того, что при вычислении из нее удаляется влияние автокорреляций с меньшими лагами (см. Бокс и Дженкинс, 1976; см. также McDowall, McCleary, Meidinger, and Hay, 1980). На лаге 1 (когда нет промежуточных элементов внутри лага), частная автокорреляция равна, очевидно, обычной автокорреляции. На самом деле, частная автокорреляция дает более " чистую" картину периодических зависимостей.
| Partial autocorrelations. Another useful method to examine serial dependencies is to examine the partial autocorrelation function (PACF) - an extension of autocorrelation, where the dependence on the intermediate elements (those within the lag) is removed. In other words the partial autocorrelation is similar to autocorrelation, except that when calculating it, the (auto) correlations with all the elements within the lag are partialled out (Box & Jenkins, 1976; see also McDowall, McCleary, Meidinger, & Hay, 1980). If a lag of 1 is specified (i. e., there are no intermediate elements within the lag), then the partial autocorrelation is equivalent to auto correlation. In a sense, the partial autocorrelation provides a " cleaner" picture of serial dependencies for individual lags (not confounded by other serial dependencies).
|
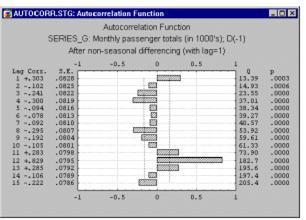
| Удаление периодической зависимости. Как отмечалось выше, периодическая составляющая для данного лага k может быть удалена взятием разности соответствующего порядка. Это означает, что из каждого i-го элемента ряда вычитается (i-k)-й элемент. Имеются два довода в пользу таких преобразований.
| Removing serial dependency. Serial dependency for a particular lag of k can be removed by differencing the series, that is converting each i'th element of the series into its difference from the (i-k)''th element. There are two major reasons for such transformations.
|
| Во-первых, таким образом можно определить скрытые периодические составляющие ряда. Напомним, что автокорреляции на последовательных лагах зависимы. Поэтому удаление некоторых автокорреляций изменит другие автокорреляции, которые, возможно, подавляли их, и сделает некоторые другие сезонные составляющие более заметными.
| First, one can identify the hidden nature of seasonal dependencies in the series. Remember that, as mentioned in the previous paragraph, autocorrelations for consecutive lags are interdependent. Therefore, removing some of the autocorrelations will change other auto correlations, that is, it may eliminate them or it may make some other seasonalities more apparent.
|
| Во-вторых, удаление сезонных составляющих делает ряд стационарным, что необходимо для применения АРПСС и других методов, например, спектрального анализа.
| The other reason for removing seasonal dependencies is to make the series stationary which is necessary for ARIMA and other techniques.
|
| АРПСС
| ARIMA
|
| • Общее введение
| |
| • Два основных процесса
| |
| • Модель АРПСС
| |
| • Идентификация
| |
| • Оценивание параметров
| |
| • Оценивание модели
| |
| Дополнительная информация о методах Анализа временных рядов дана также в следующих разделах:
| For more information on Time Series methods, see also:
|
| • Идентификация модели временных рядов
| · Identifying Patterns in Time Series Data
|
| • Прерванные временные ряды
| · Interrupted Time Series
|
| • Экспоненциальное сглаживание
| · Exponential Smoothing
|
| • Сезонная декомпозиция (метод Census I)
| · Seasonal Decomposition (Census I)
|
| • Сезонная корректировка X-11 (метод Census II)
| · X-11 Census method II seasonal adjustment
|
| • Таблицы результатов корректировки X-11
| · X-11 Census method II result tables
|
| • Анализ распределенных лагов
| · Distributed Lags Analysis
|
| • Одномерный анализ Фурье
| · Single Spectrum (Fourier) Analysis
|
| • Кросс-спектральный анализ
| · Cross-spectrum Analysis
|
| • Основные понятия и принципы
| · Basic Notations and Principles
|
| • Быстрое преобразование Фурье
| · Fast Fourier Transformations
|
| Общее введение
| General Introduction
|
| Процедуры оценки параметров и прогнозирования, описанные в разделе Идентификация модели временных рядов, предполагают, что математическая модель процесса известна. В реальных данных часто нет отчетливо выраженных регулярных составляющих. Отдельные наблюдения содержат значительную ошибку, тогда как вы хотите не только выделить регулярные компоненты, но также построить прогноз. Методология АРПСС, разработанная Боксом и Дженкинсом (1976), позволяет это сделать. Данный метод чрезвычайно популярен во многих приложениях, и практика подтвердила его мощность и гибкость (Hoff, 1983; Pankratz, 1983; Vandaele, 1983). Однако из-за мощности и гибкости, АРПСС - сложный метод. Его не так просто использовать, и требуется большая практика, чтобы овладеть им. Хотя часто он дает удовлетворительные результаты, они зависят от квалификации пользователя (Bails and Peppers, 1982). Следующие разделы познакомят вас с его основными идеями. Для интересующихся кратким, рассчитанным на применение, (нематематическим) введением в АРПСС, рекомендуем книгу McCleary, Meidinger, and Hay (1980).
| The modeling and forecasting procedures discussed in the Identifying Patterns in Time Series Data, involved knowledge about the mathematical model of the process. However, in real-life research and practice, patterns of the data are unclear, individual observations involve considerable error, and we still need not only to uncover the hidden patterns in the data but also generate forecasts. The ARIMA methodology developed by Box and Jenkins (1976) allows us to do just that; it has gained enormous popularity in many areas and research practice confirms its power and flexibility (Hoff, 1983; Pankratz, 1983; Vandaele, 1983). However, because of its power and flexibility, ARIMA is a complex technique; it is not easy to use, it requires a great deal of experience, and although it often produces satisfactory results, those results depend on the researcher's level of expertise (Bails & Peppers, 1982). The following sections will introduce the basic ideas of this methodology. For those interested in a brief, applications-oriented (non- mathematical), introduction to ARIMA methods, we recommend McDowall, McCleary, Meidinger, and Hay (1980).
|
| Два основных процесса
| Two Common Processes
|
| Процесс авторегрессии. Большинство временных рядов содержат элементы, которые последовательно зависят друг от друга. Такую зависимость можно выразить следующим уравнением:
| Autoregressive process. Most time series consist of elements that are serially dependent in the sense that one can estimate a coefficient or a set of coefficients that describe consecutive elements of the series from specific, time-lagged (previous) elements. This can be summarized in the equation:
|
| xt=ξ +Φ 1*x(t-1)+ Φ 2*x(t-2)+ Φ 3*x(t-3)+…+ε
| xt=ξ +Φ 1*x(t-1)+ Φ 2*x(t-2)+ Φ 3*x(t-3)+…+ε
|
| Здесь: ξ - константа (свободный член), Ф1, Ф2, Ф3 - параметры авторегрессии.
| Where: ξ is a constant (intercept), and Ф1, Ф2, Ф3 are the autoregressive model parameters.
|
| Вы видите, что каждое наблюдение есть сумма случайной компоненты (случайное воздействие, ε ) и линейной комбинации предыдущих наблюдений.
| Put in words, each observation is made up of a random error component (random shock, ε ) and a linear combination of prior observations.
|
| Требование стационарности. Заметим, что процесс авторегрессии будет стационарным только, если его параметры лежат в определенном диапазоне. Например, если имеется только один параметр, то он должен находиться в интервале -1< < +1. В противном случае, предыдущие значения будут накапливаться и значения последующих xt могут быть неограниченными, следовательно, ряд не будет стационарным. Если имеется несколько параметров авторегрессии, то можно определить аналогичные условия, обеспечивающие стационарность (см. например, Бокс и Дженкинс, 1976; Montgomery, 1990).
| Stationarity requirement. Note that an autoregressive process will only be stable if the parameters are within a certain range; for example, if there is only one autoregressive parameter then is must fall within the interval of -1 < φ < 1. Otherwise, past effects would accumulate and the values of successive xt' s would move towards infinity, that is, the series would not be stationary. If there is more than one autoregressive parameter, similar (general) restrictions on the parameter values can be defined (e. g., see Box & Jenkins, 1976; Montgomery, 1990).
|
| Процесс скользящего среднего. В отличие от процесса авторегрессии, в процессе скользящего среднего каждый элемент ряда подвержен суммарному воздействию предыдущих ошибок. В общем виде это можно записать следующим образом:
| Moving average process. Independent from the autoregressive process, each element in the series can also be affected by the past error (or random shock) that cannot be accounted for by the autoregressive component, that is:
|
| xt=μ +ε t-θ 1*ε (t-1)- θ 2*ε (t-2)- θ 3*ε (t-3)-…
| xt=μ +ε t-θ 1*ε (t-1)- θ 2*ε (t-2)- θ 3*ε (t-3)-…
|
| Здесь: µ - константа, θ 1, θ 2, θ 3 - параметры скользящего среднего.
| Where: µ is a constant, and θ 1, θ 2, θ 3 are the moving average model parameters.
|
| Другими словами, текущее наблюдение ряда представляет собой сумму случайной компоненты (случайное воздействие, ε ) в данный момент и линейной комбинации случайных воздействий в предыдущие моменты времени.
| Put in words, each observation is made up of a random error component (random shock, ε ) and a linear combination of prior random shocks.
|
| Обратимость. Не вдаваясь в детали, отметим, что существует " двойственность" между процессами скользящего среднего и авторегрессии (см. например, Бокс и Дженкинс, 1976; Montgomery, Johnson, and Gardiner, 1990). Это означает, что приведенное выше уравнение скользящего среднего можно переписать (обратить) в виде уравнения авторегрессии (неограниченного порядка), и наоборот. Это так называемое свойство обратимости. Имеются условия, аналогичные приведенным выше условиям стационарности, обеспечивающие обратимость модели.
| Invertibility requirement. Without going into too much detail, there is a " duality" between the moving average process and the autoregressive process (e. g., see Box & Jenkins, 1976; Montgomery, Johnson, & Gardiner, 1990), that is, the moving average equation above can be rewritten (inverted) into an autoregressive form (of infinite order). However, analogous to the stationarity condition described above, this can only be done if the moving average parameters follow certain conditions, that is, if the model is invertible. Otherwise, the series will not be stationary.
|
| Модель АРПСС
| ARIMA Methodology
|
| Модель авторегрессии и скользящего среднего. Общая модель, предложенная Боксом и Дженкинсом (1976) включает как параметры авторегрессии, так и параметры скользящего среднего. Именно, имеется три типа параметров модели: параметры авторегрессии (p), порядок разности (d), параметры скользящего среднего (q). В обозначениях Бокса и Дженкинса модель записывается как АРПСС (p, d, q). Например, модель (0, 1, 2) содержит 0 (нуль) параметров авторегрессии (p) и 2 параметра скользящего среднего (q), которые вычисляются для ряда после взятия разности с лагом 1.
| Autoregressive moving average model. The general model introduced by Box and Jenkins (1976) includes autoregressive as well as moving average parameters, and explicitly includes differencing in the formulation of the model. Specifically, the three types of parameters in the model are: the autoregressive parameters (p), the number of differencing passes (d), and moving average parameters (q). In the notation introduced by Box and Jenkins, models are summarized as ARIMA (p, d, q); so, for example, a model described as (0, 1, 2) means that it contains 0 (zero) autoregressive (p) parameters and 2 moving average (q) parameters which were computed for the series after it was differenced once.
|
| Идентификация. Как отмечено ранее, для модели АРПСС необходимо, чтобы ряд был стационарным, это означает, что его среднее постоянно, а выборочные дисперсия и автокорреляция не меняются во времени. Поэтому обычно необходимо брать разности ряда до тех пор, пока он не станет стационарным (часто также применяют логарифмическое преобразование для стабилизации дисперсии). Число разностей, которые были взяты, чтобы достичь стационарности, определяются параметром d (см. предыдущий раздел). Для того чтобы определить необходимый порядок разности, нужно исследовать график ряда и автокоррелограмму. Сильные изменения уровня (сильные скачки вверх или вниз) обычно требуют взятия несезонной разности первого порядка (лаг=1). Сильные изменения наклона требуют взятия разности второго порядка. Сезонная составляющая требует взятия соответствующей сезонной разности (см. ниже). Если имеется медленное убывание выборочных коэффициентов автокорреляции в зависимости от лага, обычно берут разность первого порядка. Однако следует помнить, что для некоторых временных рядов нужно брать разности небольшого порядка или вовсе не брать их. Заметим, что чрезмерное количество взятых разностей приводит к менее стабильным оценкам коэффициентов.
| Identification. As mentioned earlier, the input series for ARIMA needs to be stationary, that is, it should have a constant mean, variance, and autocorrelation through time. Therefore, usually the series first needs to be differenced until it is stationary (this also often requires log transforming the data to stabilize the variance). The number of times the series needs to be differenced to achieve stationarity is reflected in the d parameter (see the previous paragraph). In order to determine the necessary level of differencing, one should examine the plot of the data and autocorrelogram. Significant changes in level (strong upward or downward changes) usually require first order non seasonal (lag=1) differencing; strong changes of slope usually require second order non seasonal differencing. Seasonal patterns require respective seasonal differencing (see below). If the estimated autocorrelation coefficients decline slowly at longer lags, first order differencing is usually needed. However, one should keep in mind that some time series may require little or no differencing, and that over differenced series produce less stable coefficient estimates.
|
| На этом этапе (который обычно называют идентификацией порядка модели, см. ниже) вы также должны решить, как много параметров авторегрессии (p) и скользящего среднего (q) должно присутствовать в эффективной и экономной модели процесса. (Экономность модели означает, что в ней имеется наименьшее число параметров и наибольшее число степеней свободы среди всех моделей, которые подгоняются к данным). На практике очень редко бывает, что число параметров p или q больше 2 (см. ниже более полное обсуждение).
| At this stage (which is usually called Identification phase, see below) we also need to decide how many autoregressive (p) and moving average (q) parameters are necessary to yield an effective but still parsimonious model of the process (parsimonious means that it has the fewest parameters and greatest number of degrees of freedom among all models that fit the data). In practice, the numbers of the p or q parameters very rarely need to be greater than 2 (see below for more specific recommendations).
|
| Оценивание и прогноз. Следующий, после идентификации, шаг (Оценивание) состоит в оценивании параметров модели (для чего используются процедуры минимизации функции потерь, см. ниже; более подробная информация о процедурах минимизации дана в разделе Нелинейное оценивание). Полученные оценки параметров используются на последнем этапе (Прогноз) для того, чтобы вычислить новые значения ряда и построить доверительный интервал для прогноза. Процесс оценивания проводится по преобразованным данным (подвергнутым применению разностного оператора). До построения прогноза нужно выполнить обратную операцию (интегрировать данные). Таким образом, прогноз методологии будет сравниваться с соответствующими исходными данными. На интегрирование данных указывает буква П в общем названии модели (АРПСС = Авторегрессионное Проинтегрированное Скользящее Среднее).
| Estimation and Forecasting. At the next step (Estimation), the parameters are estimated (using function minimization procedures, see below; for more information on minimization procedures see also Nonlinear Estimation), so that the sum of squared residuals is minimized. The estimates of the parameters are used in the last stage (Forecasting) to calculate new values of the series (beyond those included in the input data set) and confidence intervals for those predicted values. The estimation process is performed on transformed (differenced) data; before the forecasts are generated, the series needs to be integrated (integration is the inverse of differencing) so that the forecasts are expressed in values compatible with the input data. This automatic integration feature is represented by the letter I in the name of the methodology (ARIMA = Auto-Regressive Integrated Moving Average).
|
| Константа в моделях АРПСС. Дополнительно модели АРПСС могут содержать константу, интерпретация которой зависит от подгоняемой модели. Именно, если (1) в модели нет параметров авторегрессии, то константа есть среднее значение ряда, если (2) параметры авторегрессии имеются, то константа представляет собой свободный член. Если бралась разность ряда, то константа представляет собой среднее или свободный член преобразованного ряда. Например, если бралась первая разность (разность первого порядка), а параметров авторегрессии в модели нет, то константа представляет собой среднее значение преобразованного ряда и, следовательно, коэффициент наклона линейного тренда исходного.
| The constant in ARIMA models. In addition to the standard autoregressive and moving average parameters, ARIMA models may also include a constant, as described above. The interpretation of a (statistically significant) constant depends on the model that is fit. Specifically, (1) if there are no autoregressive parameters in the model, then the expected value of the constant is  , the mean of the series; (2) if there are autoregressive parameters in the series, then the constant represents the intercept. If the series is differenced, then the constant represents the mean or intercept of the differenced series; For example, if the series is differenced once, and there are no autoregressive parameters in the model, then the constant represents the mean of the differenced series, and therefore the linear trend slope of the un-differenced series. , the mean of the series; (2) if there are autoregressive parameters in the series, then the constant represents the intercept. If the series is differenced, then the constant represents the mean or intercept of the differenced series; For example, if the series is differenced once, and there are no autoregressive parameters in the model, then the constant represents the mean of the differenced series, and therefore the linear trend slope of the un-differenced series.
|
| Идентификация
| Identification
|
| Число оцениваемых параметров. Конечно, до того, как начать оценивание, вам необходимо решить, какой тип модели будет подбираться к данным, и какое количество параметров присутствует в модели, иными словами, нужно идентифицировать модель АРПСС. Основными инструментами идентификации порядка модели являются графики, автокорреляционная функция (АКФ), частная автокорреляционная функция (ЧАКФ). Это решение не является простым и требуется основательно поэкспериментировать с альтернативными моделями. Тем не менее, большинство встречающихся на практике временных рядов можно с достаточной степенью точности аппроксимировать одной из 5 основных моделей (см. ниже), которые можно идентифицировать по виду автокорреляционной (АКФ) и частной автокорреляционной функции (ЧАКФ). Ниже дается список этих моделей, основанный на рекомендациях Pankratz (1983); дополнительные практические советы даны в Hoff (1983), McCleary and Hay (1980), McDowall, McCleary, Meidinger, and Hay (1980), and Vandaele (1983). Отметим, что число параметров каждого вида невелико (меньше 2), поэтому нетрудно проверить альтернативные модели.
| Number of parameters to be estimated. Before the estimation can begin, we need to decide on (identify) the specific number and type of ARIMA parameters to be estimated. The major tools used in the identification phase are plots of the series, correlograms of auto correlation (ACF), and partial autocorrelation (PACF). The decision is not straightforward and in less typical cases requires not only experience but also a good deal of experimentation with alternative models (as well as the technical parameters of ARIMA). However, a majority of empirical time series patterns can be sufficiently approximated using one of the 5 basic models that can be identified based on the shape of the autocorrelogram (ACF) and partial auto correlogram (PACF). The following brief summary is based on practical recommendations of Pankratz (1983); for additional practical advice, see also Hoff (1983), McCleary and Hay (1980), McDowall, McCleary, Meidinger, and Hay (1980), and Vandaele (1983). Also, note that since the number of parameters (to be estimated) of each kind is almost never greater than 2, it is often practical to try alternative models on the same data.
|
| 1. Один параметр (p): АКФ - экспоненциально убывает; ЧАКФ - имеет резко выделяющееся значение для лага 1, нет корреляций на других лагах.
| 1. One autoregressive (p) parameter: ACF - exponential decay; PACF - spike at lag 1, no correlation for other lags.
|
| 2. Два параметра авторегрессии (p): АКФ имеет форму синусоиды или экспоненциально убывает; ЧАКФ имеет резко выделяющиеся значения на лагах 1, 2, нет корреляций на других лагах.
| 2. Two autoregressive (p) parameters: ACF - a sine-wave shape pattern or a set of exponential decays; PACF - spikes at lags 1 and 2, no correlation for other lags.
|
| 3. Один параметр скользящего среднего (q): АКФ имеет резко выделяющееся значение на лаге 1, нет корреляций на других лагах. ЧАКФ экспоненциально убывает.
| 3. One moving average (q) parameter: ACF - spike at lag 1, no correlation for other lags; PACF - damps out exponentially.
|
| 4. Два параметра скользящего среднего (q): АКФ имеет резко выделяющиеся значения на лагах 1, 2, нет корреляций на других лагах. ЧАКФ имеет форму синусоиды или экспоненциально убывает.
| 4. Two moving average (q) parameters: ACF - spikes at lags 1 and 2, no correlation for other lags; PACF - a sine-wave shape pattern or a set of exponential decays.
|
| 5. Один параметр авторегрессии (p) и один параметр скользящего среднего (q): АКФ экспоненциально убывает с лага 1; ЧАКФ - экспоненциально убывает с лага 1.
| 5. One autoregressive (p) and one moving average (q) parameter: ACF - exponential decay starting at lag 1; PACF - exponential decay starting at lag 1.
|
| Сезонные модели. Мультипликативная сезонная АРПСС представляет естественное развитие и обобщение обычной модели АРПСС на ряды, в которых имеется периодическая сезонная компонента. В дополнении к несезонным параметрам, в модель вводятся сезонные параметры для определенного лага (устанавливаемого на этапе идентификации порядка модели). Аналогично параметрам простой модели АРПСС, эти параметры называются: сезонная авторегрессия (ps), сезонная разность (ds) и сезонное скользящее среднее (qs). Таким образом, полная сезонная АРПСС может быть записана как АРПСС (p, d, q)(ps, ds, qs). Например, модель (0, 1, 2)(0, 1, 1) включает 0 регулярных параметров авторегрессии, 2 регулярных параметра скользящего среднего и 1 параметр сезонного скользящего среднего. Эти параметры вычисляются для рядов, получаемых после взятия одной разности с лагом 1 и далее сезонной разности. Сезонный лаг, используемый для сезонных параметров, определяется на этапе идентификации порядка модели.
| Seasonal models. Multiplicative seasonal ARIMA is a generalization and extension of the method introduced in the previous paragraphs to series in which a pattern repeats seasonally over time. In addition to the non-seasonal parameters, seasonal parameters for a specified lag (established in the identification phase) need to be estimated. Analogous to the simple ARIMA parameters, these are: seasonal autoregressive (ps), seasonal differencing (ds), and seasonal moving average parameters (qs). For example, the model (0, 1, 2)(0, 1, 1) describes a model that includes no autoregressive parameters, 2 regular moving average parameters and 1 seasonal moving average parameter, and these parameters were computed for the series after it was differenced once with lag 1, and once seasonally differenced. The seasonal lag used for the seasonal parameters is usually determined during the identification phase and must be explicitly specified.
|
| Общие рекомендации относительно выбора обычных параметров (с помощью АКФ и ЧАКФ) полностью применимы к сезонным моделям. Основное отличие состоит в том, что в сезонных рядах АКФ и ЧАКФ имеют существенные значения на лагах, кратных сезонному лагу (в дополнении к характерному поведению этих функций, описывающих регулярную (несезонную) компоненту АРПСС).
| The general recommendations concerning the selection of parameters to be estimated (based on ACF and PACF) also apply to seasonal models. The main difference is that in seasonal series, ACF and PACF will show sizable coefficients at multiples of the seasonal lag (in addition to their overall patterns reflecting the non seasonal components of the series).
|
| Оценивание параметров
| Parameter Estimation
|
| Существуют различные методы оценивания параметров, которые дают очень похожие оценки, но для данной модели одни оценки могут быть более эффективны, а другие менее эффективны. В общем, во время оценивания порядка модели используется так называемый квазиньютоновский алгоритм максимизации правдоподобия (вероятности) наблюдения значений ряда по значениям параметров (см. Нелинейное оценивание). Практически это требует вычисления (условных) сумм квадратов (SS) остатков модели. Имеются различные способы вычисления суммы квадратов остатков SS; вы можете выбрать: (1) приближенный метод максимального правдоподобия МакЛеода и Сейлза (1983), (2) приближенный метод максимального правдоподобия с итерациями назад, (3)точный метод максимального правдоподобия по Meларду (1984).
| There are several different methods for estimating the parameters. All of them should produce very similar estimates, but may be more or less efficient for any given model. In general, during the parameter estimation phase a function minimization algorithm is used (the so-called quasi-Newton method; refer to the description of the Nonlinear Estimationmethod) to maximize the likelihood (probability) of the observed series, given the parameter values. In practice, this requires the calculation of the (conditional) sums of squares (SS) of the residuals, given the respective parameters. Different methods have been proposed to compute the SS for the residuals: (1) the approximate maximum likelihood method according to McLeod and Sales (1983), (2) the approximate maximum likelihood method with backcasting, and (3) the exact maximum likelihood method according to Melard (1984).
|
| Сравнение методов. В общем, все методы дают очень похожие результаты. Также все методы показали примерно одинаковую эффективность на реальных данных. Однако метод 1 (см. выше) - самый быстрый, и им можно пользоваться для исследования очень длинных рядов (например, содержащих более 30, 000 наблюдений). Метод Меларда (номер 3) может оказаться неэффективным, если оцениваются параметры сезонной модели с большим сезонным лагом (например, 365 дней). С другой стороны, вы можете использовать вначале приближенный метод максимального правдоподобия (для того, чтобы найти прикидочные оценки параметров), а затем точный метод; обычно требуется только несколько итераций точного метода (номер 3, выше), чтобы получить окончательные оценки.
| Comparison of methods. In general, all methods should yield very similar parameter estimates. Also, all methods are about equally efficient in most real-world time series applications. However, method 1 above, (approximate maximum likelihood, no backcasts) is the fastest, and should be used in particular for very long time series (e. g., with more than 30, 000 observations). Melard's exact maximum likelihood method (number 3 above) may also become inefficient when used to estimate parameters for seasonal models with long seasonal lags (e. g., with yearly lags of 365 days). On the other hand, you should always use the approximate maximum likelihood method first in order to establish initial parameter estimates that are very close to the actual final values; thus, usually only a few iterations with the exact maximum likelihood method (3, above) are necessary to finalize the parameter estimates.
|
| Стандартные ошибки оценок. Для всех оценок параметров вычисляются так называемые асимптотические стандартные ошибки, для вычисления которых используется матрица частных производных второго порядка, аппроксимируемая конечными разностями (см. также раздел Нелинейное оценивание).
| Parameter standard errors. For all parameter estimates, you will compute so-called asymptotic standard errors. These are computed from the matrix of second-order partial derivatives that is approximated via finite differencing (see also the respective discussion in Nonlinear Estimation).
|
| Штраф. Процедура оценивания минимизирует (условную) сумму квадратов остатков модели. Если модель не является адекватной, может случиться так, что оценки параметров на каком-то шаге станут неприемлемыми - очень большими (например, не удовлетворяют условию стационарности). В таком случае, SS будет приписано очень большое значение (штрафное значение). Обычно это " заставляет" итерационный процесс удалить параметры из недопустимой области. Однако в некоторых случаях и эта стратегия может оказаться неудачной, и вы все равно увидите на экране (во время процедуры оценивания) очень большие значения SS на серии итераций. В таких случаях следует с осторожностью оценивать пригодность модели. Если модель содержит много параметров и, возможно, имеется интервенция (см. ниже), то следует несколько раз испытать процесс оценивания с различными начальными. Если модель содержит много параметров и, возможно, интервенцию (см. ниже), вам следует повторить процедуру с различными начальными значениями параметров.
| Penalty value. As mentioned above, the estimation procedure requires that the (conditional) sums of squares of the ARIMA residuals be minimized. If the model is inappropriate, it may happen during the iterative estimation process that the parameter estimates become very large, and, in fact, invalid. In that case, the it will assign a very large value (a so-called penalty value) to the SS. This usually " entices" the iteration process to move the parameters away from invalid ranges. However, in some cases even this strategy fails, and you may see on the screen (during the Estimation procedure) very large values for the SS in consecutive iterations. In that case, carefully evaluate the appropriateness of your model. If your model contains many parameters, and perhaps an intervention component (see below), you may try again with different parameter start values.
|
| Оценивание модели
| Evaluation of the Model
|
| Оценки параметров. Если значения вычисляемой t статистики не значимы, соответствующие параметры в большинстве случаев удаляются из модели без ущерба подгонки.
| Parameter estimates. You will report approximate t values, computed from the parameter standard errors (see above). If not significant, the respective parameter can in most cases be dropped from the model without affecting substantially the overall fit of the model.
|
| Другой критерий качества. Другой обычной мерой надежности модели является сравнение прогноза, построенного по урезанному ряду с " известными (исходными) данными".
| Other quality criteria. Another straightforward and common measure of the reliability of the model is the accuracy of its forecasts generated based on partial data so that the forecasts can be compared with known (original) observations.
|
| 
|
| Однако качественная модель должна не только давать достаточно точный прогноз, но быть экономной и иметь независимые остатки, содержащие только шум без систематических компонент (в частности, АКФ остатков не должна иметь какой-либо периодичности). Поэтому необходим всесторонний анализ остатков. Хорошей проверкой модели являются: (a) график остатков и изучение их трендов, (b) проверка АКФ остатков (на графике АКФ обычно отчетливо видна периодичность).
| However, a good model should not only provide sufficiently accurate forecasts, it should also be parsimonious and produce statistically independent residuals that contain only noise and no systematic components (e. g., the correlogram of residuals should not reveal any serial dependencies). A good test of the model is (a) to plot the residuals and inspect them for any systematic trends, and (b) to examine the autocorrelogram of residuals (there should be no serial dependency between residuals).
|
| Анализ остатков. Если остатки систематически распределены (например, отрицательны в первой части ряда и примерно равны нуля во второй) или включают некоторую периодическую компоненту, то это свидетельствует о неадекватности модели. Анализ остатков чрезвычайно важен и необходим при анализе временных рядов. Процедура оценивания предполагает, что остатки не коррелированы и нормально распределены.
| Analysis of residuals. The major concern here is that the residuals are systematically distributed across the series (e. g., they could be negative in the first part of the series and approach zero in the second part) or that they contain some serial dependency which may suggest that the ARIMA model is inadequate. The analysis of ARIMA residuals constitutes an important test of the model. The estimation procedure assumes that the residual are not (auto-) correlated and that they are normally distributed.
|
| Ограничения. Следует напомнить, что модель АРПСС является подходящей только для рядов, которые являются стационарными (среднее, дисперсия и автокорреляция примерно постоянны во времени); для нестационарных рядов следует брать разности. Рекомендуется иметь, как минимум, 50 наблюдений в файле исходных данных. Также предполагается, что параметры модели постоянны, т. е. не меняются во времени.
| Limitations. The ARIMA method is appropriate only for a time series that is stationary (i. e., its mean, variance, and autocorrelation should be approximately constant through time) and it is recommended that there are at least 50 observations in the input data. It is also assumed that the values of the estimated parameters are constant throughout the series.
|
| Прерванные временные ряды
| Interrupted Time Series ARIMA
|
| Обычный вопрос, возникающий при анализе временных рядов, состоит в следующем, воздействует или нет внешнее событие на последовательность наблюдений. Например, привела ли новая экономическая политика к росту экономики, как обещалось; изменил ли новый закон интенсивность преступлений и т. д. В общем, нужно оценивать воздействия одного или нескольких дискретных событий на значения ряда. Этот вид анализа прерванных временных рядов подробно описан в книге McDowall, McCleary, Meidinger, and Hay (1980). Различают следующие три типа воздействий: (1) устойчивое скачкообразное, (2) устойчивое постепенное, (3) скачкообразное временное. См. также следующие разделы:
| A common research questions in time series analysis is whether an outside event affected subsequent observations. For example, did the implementation of a new economic policy improve economic performance; did the a new anti-crime law affect subsequent crime rates; and so on. In general, we would like to evaluate the impact of one or more discrete events on the values in the time series. This type of interrupted time series analysis is described in detail in McDowall, McCleary, Meidinger, & Hay (1980). McDowall, et. al., distinguish between three major types of impacts that are possible: (1) permanent abrupt, (2) permanent gradual, and (3) abrupt temporary. See also:
|
| • Идентификация модели временных рядов
| - Identifying Patterns in Time Series Data
|
| • АРПСС
| |
| • Экспоненциальное сглаживание
| |
| • Сезонная декомпозиция (метод Census I)
| - Seasonal Decomposition (Census I)
|
| • Сезонная корректировка X-11 (метод Census II)
| - X-11 Census method II seasonal adjustment
|
| • Таблицы результатов корректировки X-11
| - X-11 Census method II result tables
- Distributed Lags Analysis
|
| • Анализ распределенных лагов
| - Single Spectrum (Fourier) Analysis
|
| • Одномерный анализ Фурье
| |
| • Кросс-спектральный анализ
| - Basic Notations and Principles
|
| • Основные понятия и принципы
| - Fast Fourier Transformations
|
| • Быстрое преобразование Фурье
|
|
| Экспоненциальное сглаживание
| Exponential Smoothing
|
| • Общее введение
| · General Introduction
|
| • Простое экспоненциальное сглаживание
| · Simple Exponential Smoothing
|
| • Выбор лучшего значения параметра a (альфа)
| - Choosing the Best Value for Parameter a (alpha)
|
| • Индексы качества подгонки
| - Indices of Lack of Fit (Error)
|
| • Сезонная и несезонная модели с трендом или без тренда
| - Seasonal and Non-seasonal Models With or Without Trend
|
| См. также:
| See also:
|
| • Идентификация модели временных рядов
| Identifying Patterns in Time Series Data
|
| • АРПСС (Бокс и Дженкинс) и автокорреляции
| - ARIMA (Box & Jenkins) and Autocorrelations
|
| • Прерванные временные ряды
| |
| • Сезонная декомпозиция (метод Census I)
| - Seasonal Decomposition (Census I)
|
| • Сезонная корректировка X-11 (метод Census II)
| - X-11 Census method II seasonal adjustment
|
| • Таблицы результатов корректировки X-11
| - X-11 Census method II result tables
|
| • Анализ распределенных лагов
| - Distributed Lags Analysis
|
| • Одномерный анализ Фурье
| - Single Spectrum (Fourier) Analysis
|
| • Кросс-спектральный анализ
| |
| • Основные понятия и принципы
| - Basic Notations and Principles
|
| • Быстрое преобразование Фурье
| - Fast Fourier Transformations
|
| Общее введение
| General Introduction
|
| Экспоненциальное сглаживание - это очень популярный метод прогнозирования многих временных рядов. Исторически метод был независимо открыт Броуном и Холтом. Броун служил на флоте США во время второй мировой войны, где занимался обнаружением подводных лодок и системами наведения. Позже он применил открытый им метод для прогнозирования спроса на запасные части. Свои идеи он описал в книге, вышедшей в свет в 1959 году. Исследования Холта были поддержаны Департаментом военно-морского флота США. Независимо друг от друга, Броун и Холт открыли экспоненциальное сглаживание для процессов с постоянным трендом, с линейным трендом и для рядов с сезонной составляющей.
| Exponential smoothing has become very popular as a forecasting method for a wide variety of time series data. Historically, the method was independently developed by Brown and Holt. Brown worked for the US Navy during World War II, where his assignment was to design a tracking system for fire-control information to compute the location of submarines. Later, he applied this technique to the forecasting of demand for spare parts (an inventory control problem). He described those ideas in his 1959 book on inventory control. Holt's research was sponsored by the Office of Naval Research; independently, he developed exponential smoothing models for constant processes, processes with linear trends, and for seasonal data.
|
| Gardner (1985), предложил " единую" классификацию методов экспоненциального сглаживания. Превосходное введение в эти методы можно найти в книгах Makridakis, Wheelwright, and McGee (1983), Makridakis and Wheelwright (1989), Montgomery, Johnson, and Gardiner (1990).
| Gardner (1985) proposed a " unified" classification of exponential smoothing methods. Excellent introductions can also be found in Makridakis, Wheelwright, and McGee (1983), Makridakis and Wheelwright (1989), Montgomery, Johnson, & Gardiner (1990).
|
| Простое экспоненциальное сглаживание
| Simple Exponential Smoothing
|
| Простая и прагматически ясная модель временного ряда имеет следующий вид:
| Simple and clear pragmatic model of the time series is as follows:
|
| xt=b+ε t где b - константа и ε (эпсилон) - случайная ошибка. Константа b относительно стабильна на каждом временном интервале, но может также медленно изменяться со временем. Один из интуитивно ясных способов выделения b состоит в том, чтобы использовать сглаживание скользящим средним, в котором последним наблюдениям приписываются большие веса, чем предпоследним, предпоследним большие веса, чем пред-предпоследним и т. д. Простое экспоненциальное именно так и устроено. Здесь более старым наблюдениям приписываются экспоненциально убывающие веса, при этом, в отличие от скользящего среднего, учитываются все предшествующие наблюдения ряда, а не те, что попали в определенное окно. Точная формула простого экспоненциального сглаживания имеет следующий вид:
| Xt = b + 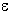 t. The constant b is relatively stable in each segment of the series, but may change slowly over time. If appropriate, then one way to isolate the true value of b, and thus the systematic or predictable part of the series, is to compute a kind of moving average, where the current and immediately preceding (" younger" ) observations are assigned greater weight than the respective older observations. Simple exponential smoothing accomplishes exactly such weighting, where exponentially smaller weights are assigned to older observations. The specific formula for simple exponential smoothing is: t. The constant b is relatively stable in each segment of the series, but may change slowly over time. If appropriate, then one way to isolate the true value of b, and thus the systematic or predictable part of the series, is to compute a kind of moving average, where the current and immediately preceding (" younger" ) observations are assigned greater weight than the respective older observations. Simple exponential smoothing accomplishes exactly such weighting, where exponentially smaller weights are assigned to older observations. The specific formula for simple exponential smoothing is:
|
| St=α *xt+(1-α )* St-1
| St=α *xt+(1-α )* St-1
|
| Когда эта формула применяется рекурсивно, то каждое новое сглаженное значение (которое является также прогнозом) вычисляется как взвешенное среднее текущего наблюдения и сглаженного ряда. Очевидно, результат сглаживания зависит от параметра α (альфа). Если α равно 1, то предыдущие наблюдения полностью игнорируются. Если α равно 0, то игнорируются текущие наблюдения. Значения α между 0, 1 дают промежуточные результаты.
| When applied recursively to each successive observation in the series, each new smoothed value (forecast) is computed as the weighted average of the current observation and the previous smoothed observation; the previous smoothed observation was computed in turn from the previous observed value and the smoothed value before the previous observation, and so on. Thus, in effect, each smoothed value is the weighted average of the previous observations, where the weights decrease exponentially depending on the value of parameter α (alpha). If α is equal to 1 (one) then the previous observations are ignored entirely; if α is equal to 0 (zero), then the current observation is ignored entirely, and the smoothed value consists entirely of the previous smoothed value (which in turn is computed from the smoothed observation before it, and so on; thus all smoothed values will be equal to the initial smoothed value S0). Values of α in-between will produce intermediate results.
|
| Эмпирические исследования Makridakis и др. (1982; Makridakis, 1983) показали, что весьма часто простое экспоненциальное сглаживание дает достаточно точный прогноз.
| empirical research by Makridakis et al. (1982, Makridakis, 1983), has shown simple exponential smoothing to be the best choice for one-period-ahead forecasting.
|
| Выбор лучшего значения параметра α (альфа)
| Choosing the Best Value for Parameter α (alpha)
|
| Gardner (1985) обсуждает различные теоретические и эмпирические аргументы в пользу выбора определенного параметра сглаживания. Очевидно, из формулы, приведенной выше, следует, что α должно попадать в интервал между 0 (нулем) и 1 (хотя Brenner et al., 1968, для дальнейшего применения анализа АРПСС считают, что 0< α < 2). Gardner (1985) сообщает, что на практике обычно рекомендуется брать α меньше . 30. Однако в исследовании Makridakis et al., (1982), α большее . 30, часто дает лучший прогноз. После обзора литературы, Gardner (1985) приходит к выводу, что лучше оценивать оптимально α по данным (см. ниже), чем просто " гадать" или использовать искусственные рекомендации.
| Gardner (1985) discusses various theoretical and empirical arguments for selecting an appropriate smoothing parameter. Obviously, looking at the formula presented above, α should fall into the interval between 0 (zero) and 1 (although, see Brenner et al. , 1968, for an ARIMA perspective, implying 0< α < 2). Gardner (1985) reports that among practitioners, an α smaller than. 30 is usually recommended. However, in the study by Makridakis et al. (1982), α values above. 30 frequently yielded the best forecasts. After reviewing the literature on this topic, Gardner (1985) concludes that it is best to estimate an optimum α from the data (see below), rather than to " guess" and set an artificially low value.
|
| Оценивание лучшего значенияα с помощью данных. На практике параметр сглаживания часто ищется с поиском на сетке. Возможные значения параметра разбиваются сеткой с определенным шагом. Например, рассматривается сетка значений от α = 0. 1 до α = 0. 9, с шагом 0. 1. Затем выбирается α, для которого сумма квадратов (или средних квадратов) остатков (наблюдаемые значения минус прогнозы на шаг вперед) является минимальной.
| Estimating the best α value from the data. In practice, the smoothing parameter is often chosen by a grid search of the parameter space; that is, different solutions for α are tried starting, for example, with α = 0. 1 to α = 0. 9, with increments of 0. 1. Then α is chosen so as to produce the smallest sums of squares (or mean squares) for the residuals (i. e., observed values minus one-step-ahead forecasts; this mean squared error is also referred to as ex post mean squared error, ex post MSE for short).
|
| Индексы качества подгонки
| Indices of Lack of Fit (Error)
|
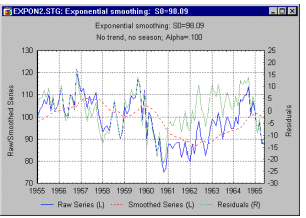
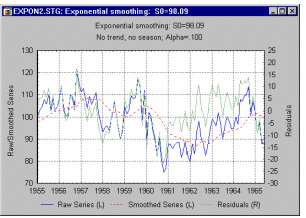
| Самый прямой способ оценки прогноза, полученного на основе определенного значения α - построить график наблюдаемых значений и прогнозов на один шаг вперед. Этот график включает в себя также остатки (отложенные на правой оси Y). Из графика ясно видно, на каких участках прогноз лучше или хуже.
| The most straightforward way of evaluating the accuracy of the forecasts based on a particular α value is to simply plot the observed values and the one-step-ahead forecasts. This plot can also include the residuals (scaled against the right Y-axis), so that regions of better or worst fit can also easily be identified.
|
| 
|
| Такая визуальная проверка точности прогноза часто дает наилучшие результаты. Имеются также другие меры ошибки, которые можно использовать для определения оптимального параметра α (см. Makridakis, Wheelwright, and McGee, 1983):
| This visual check of the accuracy of forecasts is often the most powerful method for determining whether or not the current exponential smoothing model fits the data. In addition, besides the ex post MSE criterion (see previous paragraph), there are other statistical measures of error that can be used to determine the optimum α parameter (see Makridakis, Wheelwright, and McGee, 1983):
|
| Средняя ошибка. Средняя ошибка (СО) вычисляется простым усреднением ошибок на каждом шаге. Очевидным недостатком этой меры является то, что положительные и отрицательные ошибки аннулируют друг друга, поэтому она не является хорошим индикатором качества прогноза.
| Mean error: The mean error (ME) value is simply computed as the average error value (average of observed minus one-step-ahead forecast). Obviously, a drawback of this measure is that positive and negative error values can cancel each other out, so this measure is not a very good indicator of overall fit.
|
| Средняя абсолютная ошибка. Средняя абсолютная ошибка (САО) вычисляется как среднее абсолютных ошибок. Если она равна 0 (нулю), то имеем совершенную подгонку (прогноз). В сравнении со средней квадратической ошибкой, эта мера " не придает слишком большого значения" выбросам.
| Mean absolute error: The mean absolute error (MAE) value is computed as the average absolute error value. If this value is 0 (zero), the fit (forecast) is perfect. As compared to the mean squared error value, this measure of fit will " de-emphasize" outliers, that is, unique or rare large error values will affect the MAE less than the MSE value.
|
| Сумма квадратов ошибок (SSE), среднеквадратическая ошибка. Эти величины вычисляются как сумма (или среднее) квадратов ошибок. Это наиболее часто используемые индексы качества подгонки.
| Sum of squared error (SSE), Mean squared error. These values are computed as the sum (or average) of the squared error values. This is the most commonly used lack-of-fit indicator in statistical fitting procedures.
|
| Относительная ошибка (ОО). Во всех предыдущих мерах использовались действительные значения ошибок. Представляется естественным выразить индексы качества подгонки в терминах относительных ошибок. Например, при прогнозе месячных продаж, которые могут сильно флуктуировать (например, по сезонам) из месяца в месяц, вы можете быть вполне удовлетворены прогнозом, если он имеет точность? 10%. Иными словами, при прогнозировании абсолютная ошибка может быть не так интересна как относительная. Чтобы учесть относительную ошибку, было предложено несколько различных индексов (см. Makridakis, Wheelwright, and McGee, 1983). В первом относительная ошибка вычисляется как:
| Percentage error (PE). All the above measures rely on the actual error value. It may seem reasonable to rather express the lack of fit in terms of the relative deviation of the one-step-ahead forecasts from the observed values, that is, relative to the magnitude of the observed values. For example, when trying to predict monthly sales that may fluctuate widely (e. g., seasonally) from month to month, we may be satisfied if our prediction " hits the target" with about ±10% accuracy. In other words, the absolute errors may be not so much of interest as are the relative errors in the forecasts. To assess the relative error, various indices have been proposed (see Makridakis, Wheelwright, and McGee, 1983). The first one, the percentage error value, is computed as:
|
| Ο Ο t=100*(Xt-Ft)/Xt
| PEt = 100*(Xt - Ft )/Xt
|
| где Xt - наблюдаемое значение в момент времени t, и Ft - прогноз (сглаженное значение).
| where Xt is the observed value at time t, and Ft is the forecasts (smoothed values).
|
| Средняя относительная ошибка (СОО). Это значение вычисляется как среднее относительных ошибок.
| Mean percentage error (MPE). This value is computed as the average of the PE values.
|
| Средняя абсолютная относительная ошибка (САОО). Как и в случае с обычной средней ошибкой отрицательные и положительные относительные ошибки будут подавлять друг друга. Поэтому для оценки качества подгонки в целом (для всего ряда) лучше использовать среднюю абсолютную относительную ошибку. Часто эта мера более выразительная, чем среднеквадратическая ошибка. Например, знание того, что точность прогноза ±5%, полезно само по себе, в то время как значение 30. 8 для средней квадратической ошибки не может быть так просто проинтерпретировано.
| Mean absolute percentage error (MAPE). As is the case with the mean error value (ME, see above), a mean percentage error near 0 (zero) can be produced by large positive and negative percentage errors that cancel each other out. Thus, a better measure of relative overall fit is the mean absolute percentage error. Also, this measure is usually more meaningful than the mean squared error. For example, knowing that the average forecast is " off" by ±5% is a useful result in and of itself, whereas a mean squared error of 30. 8 is not immediately interpretable.
|
| Автоматический поиск лучшего параметра. Для минимизации средней квадратической ошибки, средней абсолютной ошибки или средней абсолютной относительной ошибки используется квази-ньютоновская процедура (та же, что и в АРПСС). В большинстве случаев эта процедура более эффективна, чем обычный перебор на сетке (особенно, если параметров сглаживания несколько), и оптимальное значение α можно быстро найти.
| Automatic search for best parameter. A quasi-Newton function minimization procedure (the same as in ARIMA is used to minimize either the mean squared error, mean absolute error, or mean absolute percentage error. In most cases, this procedure is more efficient than the grid search (particularly when more than one parameter must be determined), and the optimum 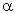 parameter can quickly be identified. parameter can quickly be identified.
|
| Первое сглаженное значениеS0. Если вы взгляните снова на формулу простого экспоненциального сглаживания, то увидите, что следует иметь значение S0 для вычисления первого сглаженного значения (прогноза). В зависимости от выбора параметра α (в частности, если α близко к 0), начальное значение сглаженного процесса может оказать существенное воздействие на прогноз для многих последующих наблюдений. Как и в других рекомендациях по применению экспоненциального сглаживания, рекомендуется брать начальное значение, дающее наилучший прогноз. С другой стороны, влияние выбора уменьшается с длиной ряда и становится некритичным при большом числе наблюдений.
| The first smoothed value S0. A final issue that we have neglected up to this point is the problem of the initial value, or how to start the smoothing process. If you look back at the formula above, it is evident that one needs an S0 value in order to compute the smoothed value (forecast) for the first observation in the series. Depending on the choice of the 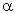 parameter (i. e., when α is close to zero), the initial value for the smoothing process can affect the quality of the forecasts for many observations. As with most other aspects of exponential smoothing it is recommended to choose the initial value that produces the best forecasts. On the other hand, in practice, when there are many leading observations prior to a crucial actual forecast, the initial value will not affect that forecast by much, since its effect will have long " faded" from the smoothed series (due to the exponentially decreasing weights, the older an observation the less it will influence the forecast). parameter (i. e., when α is close to zero), the initial value for the smoothing process can affect the quality of the forecasts for many observations. As with most other aspects of exponential smoothing it is recommended to choose the initial value that produces the best forecasts. On the other hand, in practice, when there are many leading observations prior to a crucial actual forecast, the initial value will not affect that forecast by much, since its effect will have long " faded" from the smoothed series (due to the exponentially decreasing weights, the older an observation the less it will influence the forecast).
|
| Сезонная и несезонная модели с трендом или без тренда
| Seasonal and Non-seasonal Models With or Without Trend
|
| В дополнение к простому экспоненциальному сглаживанию, были предложены более сложные модели, включающие сезонную компоненту и трендом. Общая идея таких моделей состоит в том, что прогнозы вычисляются не только по предыдущим наблюдениям (как в простом экспоненциальном сглаживании), но и с некоторыми задержками, что позволяет независимо оценить тренд и сезонную составляющую. Gardner (1985) обсудил различные модели в терминах сезонности (отсутствует, аддитивная сезонность, мультипликативная) и тренда (отсутствует, линейный тренд, экспоненциальный, демпфированный).
| The discussion above in the context of simple exponential smoothing introduced the basic procedure for identifying a smoothing parameter, and for evaluating the goodness-of-fit of a model. In addition to simple exponential smoothing, more complex models have been developed to accommodate time series with seasonal and trend components. The general idea here is that forecasts are not only computed from consecutive previous observations (as in simple exponential smoothing), but an independent (smoothed) trend and seasonal component can be added. Gardner (1985) discusses the different models in terms of seasonality (none, additive, or multiplicative) and trend (none, linear, exponential, or damped).
|
| Аддитивная и мультипликативная сезонность. Многие временные ряды имеют сезонные компоненты. Например, продажи игрушек имеют пики в ноябре, декабре и, возможно, летом, когда дети находятся на отдыхе. Эта периодичность имеет место каждый год. Однако относительный размер продаж может слегка изменяться из года в год. Таким образом, имеет смысл независимо экспоненциально сгладить сезонную компоненту с дополнительным параметром, обычно обозначаемым как δ (дельта). Сезонные компоненты, по природе своей, могут быть аддитивными или мультипликативными. Например, в течение декабря продажи определенного вида игрушек увеличиваются на 1 миллион долларов каждый год. Для того чтобы учесть сезонное колебание, вы можете добавить в прогноз на каждый декабрь 1 миллион долларов (сверх соответствующего годового среднего). В этом случае сезонность - аддитивная. Альтернативно, пусть в декабре продажи увеличились на 40%, т. е. в 1. 4 раза. Тогда, если общие продажи малы, то абсолютное (в долларах) увеличение продаж в декабре тоже относительно мало (процент роста константа). Если в целом продажи большие, то абсолютное (в долларах) увеличение продаж будет пропорционально больше. Снова, в этом случае продажи увеличатся в определенное число раз, и сезонность будет мультипликативной (в данном случае мультипликативная сезонная составляющая была бы равна 1. 4). На графике различие между двумя видами сезонности состоит в том, что в аддитивной модели сезонные флуктуации не зависят от значений ряда, тогда как в мультипликативной модели величина сезонных флуктуаций зависит от значений временного ряда.
| Additive and multiplicative seasonality. Many time series data follow recurring seasonal patterns. For example, annual sales of toys will probably peak in the months of November and December, and perhaps during the summer (with a much smaller peak) when children are on their summer break. This pattern will likely repeat every year, however, the relative amount of increase in sales during December may slowly change from year to year. Thus, it may be useful to smooth the seasonal component independently with an extra parameter, usually denoted as 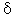 (delta). Seasonal components can be additive in nature or multiplicative. For example, during the month of December the sales for a particular toy may increase by 1 million dollars every year. Thus, we could add to our forecasts for every December the amount of 1 million dollars (over the respective annual average) to account for this seasonal fluctuation. In this case, the seasonality is additive. Alternatively, during the month of December the sales for a particular toy may increase by 40%, that is, increase by a factor of 1. 4. Thus, when the sales for the toy are generally weak, than the absolute (dollar) increase in sales during December will be relatively weak (but the percentage will be constant); if the sales of the toy are strong, than the absolute (dollar) increase in sales will be proportionately greater. Again, in this case the sales increase by a certain factor, and the seasonal component is thus multiplicative in nature (i. e., the multiplicative seasonal component in this case would be 1. 4). In plots of the series, the distinguishing characteristic between these two types of seasonal components is that in the additive case, the series shows steady seasonal fluctuations, regardless of the overall level of the series; in the multiplicative case, the size of the seasonal fluctuations vary, depending on the overall level of the series. (delta). Seasonal components can be additive in nature or multiplicative. For example, during the month of December the sales for a particular toy may increase by 1 million dollars every year. Thus, we could add to our forecasts for every December the amount of 1 million dollars (over the respective annual average) to account for this seasonal fluctuation. In this case, the seasonality is additive. Alternatively, during the month of December the sales for a particular toy may increase by 40%, that is, increase by a factor of 1. 4. Thus, when the sales for the toy are generally weak, than the absolute (dollar) increase in sales during December will be relatively weak (but the percentage will be constant); if the sales of the toy are strong, than the absolute (dollar) increase in sales will be proportionately greater. Again, in this case the sales increase by a certain factor, and the seasonal component is thus multiplicative in nature (i. e., the multiplicative seasonal component in this case would be 1. 4). In plots of the series, the distinguishing characteristic between these two types of seasonal components is that in the additive case, the series shows steady seasonal fluctuations, regardless of the overall level of the series; in the multiplicative case, the size of the seasonal fluctuations vary, depending on the overall level of the series.
|
| Параметр сезонного сглаживанияδ. В общем, прогноз на один шаг вперед вычисляется следующим образом (для моделей без тренда; для моделей с линейным и экспоненциальным трендом, тренд добавляется; см. ниже):
| The seasonal smoothing parameter δ. In general the one-step-ahead forecasts are computed as (for no trend models, for linear and exponential trend models a trend component is added to the model; see below):
|
| Аддитивная модель:
| Additive model:
|
| Прогнозt = St + It-p
| Forecastt = St + It-p
|
| Мультипликативная модель:
| Multiplicative model:
|
| Прогнозt = St*It-p
| Forecastt = St*It-p
|
| В этой формуле St обозначает (простое) экспоненциально сглаженное значение ряда в момент t, и It-p обозначает сглаженный сезонный фактор в момент t минус p (p - длина сезона). Таким образом, в сравнении с простым экспоненциальным сглаживанием, прогноз " улучшается" добавлением или умножением сезонной компоненты. Эта компонента оценивается независимо с помощью простого экспоненциального сглаживания следующим образом:
| In this formula, St stands for the (simple) exponentially smoothed value of the series at time t, and It-p stands for the smoothed seasonal factor at time t minus p (the length of the season). Thus, compared to simple exponential smoothing, the forecast is " enhanced" by adding or multiplying the simple smoothed value by the predicted seasonal component. This seasonal component is derived analogous to the St value from simple exponential smoothing as:
|
| Аддитивная модель:
| Additive model:
|
| It = It-p + δ *(1-α )*et
| It = It-p + δ *(1-α )*et
|
| Мультипликативная модель:
| Multiplicative model:
|
| It = It-p + δ *(1-α )*et/St
| It = It-p + δ *(1-α )*et/St
|
| Обратите внимание, что предсказанная сезонная компонента в момент t вычисляется, как соответствующая компонента на последнем сезонном цикле плюс ошибка (et, наблюдаемое минус прогнозируемое значение в момент t). Ясно, что параметр δ принимает значения между 0 и 1. Если он равен нулю, то сезонная составляющая на следующем цикле та же, что и на предыдущем. Если δ равен 1, то сезонная составляющая " максимально" меняется на каждом шаге из-за соответствующей ошибки (множитель (1-α ) не рассматривается из-за краткости введения). В большинстве случаев, когда сезонность присутствует, оптимальное значение δ лежит между 0 и 1.
| Put in words, the predicted seasonal component at time t is computed as the respective seasonal component in the last seasonal cycle plus a portion of the error (et; the observed minus the forecast value at time t). Considering the formulas above, it is clear that parameter δ can assume values between 0 and 1. If it is zero, then the seasonal component for a particular point in time is predicted to be identical to the predicted seasonal component for the respective time during the previous seasonal cycle, which in turn is predicted to be identical to that from the previous cycle, and so on. Thus, if δ is zero, a constant unchanging seasonal component is used to generate the one-step-ahead forecasts. If the δ parameter is equal to 1, then the seasonal component is modified " maximally" at every step by the respective forecast error (times (1-α ), which we will ignore for the purpose of this brief introduction). In most cases, when seasonality is present in the time series, the optimum δ parameter will fall somewhere between 0 (zero) and 1(one).
|
| Линейный, экспоненциальный, демпфированный тренд. Возвращаясь к примеру с игрушками, мы можем увидеть наличие линейного тренда (например, каждый год продажи увеличивались на 1 миллион), экспоненциального (например, каждый год продажи возрастают в 1. 3 раза) или демпфированного тренда (в первом году продажи возросли на 1 миллион долларов; во втором увеличение составило только 80% по сравнению с предыдущим, т. е. на $800, 000; в следующем году вновь увеличение было только на 80%, т. е. на $800, 000 *. 8 = $640, 000 и т. д. ). Каждый тип тренда по-своему проявляется в данных. В целом изменение тренда - медленное в течение времени, и опять (как и сезонную компоненту) имеет смысл экспоненциально сгладить его с отдельным параметром [обозначаемым γ (гамма) - для линейного и экспоненциального тренда, φ (фи) - для демпфированного тренда].
| Linear, exponential, and damped trend. To remain with the toy example above, the sales for a toy can show a linear upward trend (e. g., each year, sales increase by 1 million dollars), exponential growth (e. g., each year, sales increase by a factor of 1. 3), or a damped trend (during the first year sales increase by 1 million dollars; during the second year the increase is only 80% over the previous year, i. e., $800, 000; during the next year it is again 80% less than the previous year, i. e., $800, 000 *. 8 = $640, 000; etc. ). Each type of trend leaves a clear " signature" that can usually be identified in the series; shown below in the brief discussion of the different models are icons that illustrate the general patterns. In general, the trend factor may change slowly over time, and, again, it may make sense to smooth the trend component with a separate parameter (denoted γ [gamma] for linear and exponential trend models, and φ [phi] for damped trend models).
|
| Параметры сглаживания γ (линейный и экспоненциальный тренд) и φ (демпфированный тренд). Аналогично сезонной компоненте компонента тренда включается в процесс экспоненциального сглаживания. Сглаживание ее производится в каждый момент времени независимо от других компонент с соответствующими параметрами. Если γ равно 0, то тренд постоянен для всех значений временного ряда (и для всех прогнозов). Если γ равно 1, то тренд " максимально" определяется ошибками наблюдений. Параметр учитывает, как сильно изменяется тренд, т. е. как быстро он " демпфируется" или, наоборот, возрастает.
| The trend smoothing parameters γ (linear and exponential trend) and φ (damped trend). Analogous to the seasonal component, when a trend component is included in the exponential smoothing process, an independent trend component is computed for each time, and modified as a function of the forecast error and the respective parameter. If the γ parameter is 0 (zero), than the trend component is constant across all values of the time series (and for all forecasts). If the parameter is 1, then the trend component is modified " maximally" from observation to observation by the respective forecast error. Parameter values that fall in-between represent mixtures of those two extremes. Parameter φ is a trend modification parameter, and affects how strongly changes in the trend will affect estimates of the trend for subsequent forecasts, that is, how quickly the trend will be " damped" or increased.
|
| В начало
|
|
| Сезонная декомпозиция (метод Census I)
|
|
| • Общее введение
| Classical Seasonal Decomposition (Census Method 1)
|
| • Вычисления
| |
| См. также:
| |
| • Идентификация модели временных рядов
| See also:
|
| • АРПСС (Бокс и Дженкинс) и автокорреляции
| - Identifying Patterns in Time Series Data
|
| • Прерванные временные ряды
| - ARIMA (Box & Jenkins) and Autocorrelations
|
| • Экспоненциальное сглаживание
| |
| • Сезонная корректировка X-11 (метод Census II)
| |
| • Таблицы результатов корректировки X-11
| - X-11 Census method II seasonal adjustment
|
| • Анализ распределенных лагов
| - X-11 Census method II result tables
|
| • Одномерный анализ Фурье
| - Distributed Lags Analysis
|
| • Кросс-спектральный анализ
| - Single Spectrum (Fourier) Analysis
|
| • Основные понятия и принципы
| |
| • Быстрое преобразование Фурье
| - Basic Notations and Principles
|
|
| - Fast Fourier Transformations
|
| Общее введение
| General Introduction
|
| Предположим, что у вас имеются ежемесячные данные о пассажиропотоке на международных авиалиниях за 12 лет (см. Бокс и Дженкинс, 1976). Если изобразить эти данные на графике, то будет хорошо видно, что (1) объем пассажиропотока имеет во времени возрастающий линейный тренд, и (2) в ряде имеется ежегодно повторяющаяся закономерность - сезонность (большинство перевозок приходится на летние месяцы, кроме того, имеется пик меньшей высоты в районе декабрьских каникул). Цель сезонной декомпозиции и корректировки как раз и состоит в том, чтобы отделить эти компоненты, то есть разложить ряд на составляющую тренда, сезонную компоненту и оставшуюся нерегулярную составляющую. " Классический" прием, позволяющий выполнить такую декомпозицию, известен как метод Census I. Этот метод описывается и обсуждается в работах Makridakis, Wheelwright, and McGee (1983) и Makridakis and Wheelwright (1989).
| Suppose you recorded the monthly passenger load on international flights for a period of 12 years ( see Box & Jenkins, 1976). If you plot those data, it is apparent that (1) there appears to be a linear upwards trend in the passenger loads over the years, and (2) there is a recurring pattern or seasonality within each year (i. e., most travel occurs during the summer months, and a minor peak occurs during the December holidays). The purpose of the seasonal decomposition method is to isolate those components, that is, to de-compose the series into the trend effect, seasonal effects, and remaining variability. The " classic" technique designed to accomplish this decomposition is known as the Census I method. This technique is described and discussed in detail in Makridakis, Wheelwright, and McGee (1983), and Makridakis and Wheelwright (1989).
|
| Общая модель. Основная идея сезонной декомпозиции проста. В общем случае временной ряд типа того, который описан выше, можно представить себе состоящим из четырех различных компонент: (1) сезонной компоненты (обозначается St, где t обозначает момент времени), (2) тренда (Tt), (3) циклической компоненты (Ct) и (4) случайной, нерегулярной компоненты или флуктуации (It). Разница между циклической и сезонной компонентой состоит в том, что последняя имеет регулярную (сезонную) периодичность, тогда как циклические факторы обычно имеют более длительный эффект, который к тому же меняется от цикла к циклу. В методе Census I тренд и циклическую компоненту обычно объединяют в одну тренд-циклическую компоненту (TCt). Конкретные функциональные взаимосвязи между этими компонентами могут иметь самый разный вид. Однако, можно выделить два основных способа, с помощью которых они могут взаимодействовать: аддитивно и мультипликативно:
| General model. The general idea of seasonal decomposition is straightforward. In general, a time series like the one described above can be thought of as consisting of four different components: (1) A seasonal component (denoted as St, where t stands for the particular point in time) (2) a trend component (Tt), (3) a cyclical component (Ct), and (4) a random, error, or irregular component (It). The difference between a cyclical and a seasonal component is that the latter occurs at regular (seasonal) intervals, while cyclical factors have usually a longer duration that varies from cycle to cycle. In the Census I method, the trend and cyclical components are customarily combined into a trend-cycle component (TCt). The specific functional relationship between these components can assume different forms. However, two straightforward possibilities are that they combine in an additive or a multiplicative fashion:
|
| Аддитивная модель:
| Additive model:
|
| Xt = TCt + St + It
| Xt = TCt + St + It
|
| Мультипликативная модель:
| Multiplicative model:
|
| Xt = Tt*Ct*St*It
| Xt = Tt*Ct*St*It
|
| Здесь Xt обозначает значение временного ряда в момент времени t. Если имеются какие-то априорные сведения о циклических факторах, влияющих на ряд (например, циклы деловой конъюнктуры), то можно использовать оценки для различных компонент для составления прогноза будущих значений ряда. (Однако для прогнозирования предпочтительнее экспоненциальное сглаживание, позволяющее учитывать сезонную составляющую и тренд. )
| Here Xt stands for the observed value of the time series at time t. Given some a priori knowledge about the cyclical factors affecting the series (e. g., business cycles), the estimates for the different components can be used to compute forecasts for future observations. (However, the Exponential smoothing method, which can also incorporate seasonality and trend components, is the preferred technique for forecasting purposes. )
|
| Аддитивная и мультипликативная сезонность. Рассмотрим на примере различие между аддитивной и мультипликативной сезонными компонентами. График объема продаж детских игрушек, вероятно, будет иметь ежегодный пик в ноябре-декабре, и другой - существенно меньший по высоте - в летние месяцы, приходящийся на каникулы. Такая сезонная закономерность будет повторяться каждый год. По своей природе сезонная компонента может быть аддитивной или мультипликативной. Так, например, каждый год объем продаж некоторой конкретной игрушки может увеличиваться в декабре на 3 миллиона долларов. Поэтому вы можете учесть эти сезонные изменения, прибавляя к своему прогнозу на декабрь 3 миллиона. Здесь мы имеем аддитивную сезонность. Может получиться иначе. В декабре объем продаж некоторой игрушки может увеличиваться на 40%, то есть умножаться на множитель 1. 4. Это значит, например, что если средний объем продаж этой игрушки невелик, то абсолютное (в денежном выражении) увеличение этого объема в декабре также будет относительно небольшим (но в процентном исчислении оно будет постоянным); если же игрушка продается хорошо, то и абсолютный (в долларах) рост объема продаж будет значительным. Здесь опять, объем продаж возрастает в число раз, равное определенному множителю, а сезонная компонента, по своей природе, мультипликативная компонента (в данном случае равная 1. 4). Если перейти к графикам временных рядов, то различие между этими двумя видами сезонности будет проявляться так: в аддитивном случае ряд будет иметь постоянные сезонные колебания, величина которых не зависит от общего уровня значений ряда; в мультипликативном случае величина сезонных колебаний будет меняться в зависимости от общего уровня значений ряда.
| Additive and multiplicative seasonality. Let us consider the difference between an additive and multiplicative seasonal component in an example: The annual sales of toys will probably peak in the months of November and December, and perhaps during the summer (with a much smaller peak) when children are on their summer break. This seasonal pattern will likely repeat every year. Seasonal components can be additive or multiplicative in nature. For example, during the month of December the sales for a particular toy may increase by 3 million dollars every year. Thus, we could add to our forecasts for every December the amount of 3 million to account for this seasonal fluctuation. In this case, the seasonality is additive. Alternatively, during the month of December the sales for a particular toy may increase by 40%, that is, increase by a factor of 1. 4. Thus, when the sales for the toy are generally weak, then the absolute (dollar) increase in sales during December will be relatively weak (but the percentage will be constant); if the sales of the toy are strong, then the absolute (dollar) increase in sales will be proportionately greater. Again, in this case the sales increase by a certain factor, and the seasonal component is thus multiplicative in nature (i. e., the multiplicative seasonal component in this case would be 1. 4). In plots of series, the distinguishing characteristic between these two types of seasonal components is that in the additive case, the series shows steady seasonal fluctuations, regardless of the overall level of the series; in the multiplicative case, the size of the seasonal fluctuations vary, depending on the overall level of the series.
|
| Аддитивный и мультипликативный тренд-цикл. Рассмотренный пример можно расширить, чтобы проиллюстрировать понятия аддитивной и мультипликативной тренд-циклических компонент. В случае с игрушками, тренд " моды" может привести к устойчивому росту продаж (например, это может быть общий тренд в сторону игрушек образовательной направленности). Как и сезонная компонента, этот тренд может быть по своей природе аддитивным (продажи ежегодно увеличиваются на 3 миллиона долларов) или мультипликативным (продажи ежегодно увеличиваются на 30%, или возрастают в 1. 3 раза). Кроме того, объем продаж может содержать циклические компоненты. Повторим еще раз, что циклическая компонента отличается от сезонной тем, что она обычно имеет большую временную протяженность и проявляется через неравные промежутки времени. Так, например, некоторая игрушка может быть особенно " горячей" в течение летнего сезона (например, кукла, изображающая персонаж популярного мультфильма, которая к тому же агрессивно рекламируется). Как и в предыдущих случаях, такая циклическая компонента может изменять объем продаж аддитивно, либо мультипликативно.
| Additive and multiplicative trend-cycle. We can extend the previous example to illustrate the additive and multiplicative trend-cycle components. In terms of our toy example, a " fashion" trend may produce a steady increase in sales (e. g., a trend towards more educational toys in general); as with the seasonal component, this trend may be additive (sales increase by 3 million dollars per year) or multiplicative (sales increase by 30%, or by a factor of 1. 3, annually) in nature. In addition, cyclical components may impact sales; to reiterate, a cyclical component is different from a seasonal component in that it usually is of longer duration, and that it occurs at irregular intervals. For example, a particular toy may be particularly " hot" during a summer season (e. g., a particular doll which is tied to the release of a major children's movie, and is promoted with extensive advertising). Again such a cyclical component can effect sales in an additive manner or multiplicative manner.
|
| Вычисления
| Computations
|
| В вычислительном отношении процедура метода Сезонной декомпозиции (Census I) следует стандартным формулам, см. Makridakis, Wheelwright, and McGee (1983) или Makridakis and Wheelwright (1989).
| The Seasonal Decomposition (Census I) standard formulas are shown in Makridakis, Wheelwright, and McGee (1983), and Makridakis and Wheelwright (1989).
|
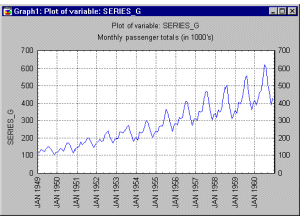
| 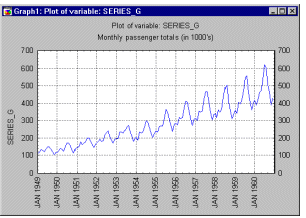
|
| Скользящее среднее. Сначала вычисляется скользящее среднее для временного ряда, при этом ширина окна берется равной периоду сезонности. Если период сезонности - четное число, пользователь может выбрать одну из двух возможностей: брать скользящее среднее с одинаковыми весами или же с неравными весами так, что первое и последнее наблюдения в окне имеют усредненные веса.
| Moving average. First a moving average is computed for the series, with the moving average window width equal to the length of one season. If the length of the season is even, then the user can choose to use either equal weights for the moving average or unequal weights can be used, where the first and last observation in the moving average window are averaged.
|
| Отношения или разности. После взятия скользящих средних вся сезонная (т. е. внутри сезона) изменчивость будет исключена, и поэтому разность (в случае аддитивной модели) или отношение (для мультипликативной модели) между наблюдаемым и сглаженным рядом будет выделять сезонную составляющую (плюс нерегулярную компоненту). Более точно, ряд скользящих средних вычитается из наблюдаемого ряда (в аддитивной модели) или же значения наблюдаемого ряда делятся на значения скользящих средних (в мультипликативной модели).
| Ratios or differences. In the moving average series, all seasonal (within-season) variability will be eliminated; thus, the differences (in additive models) or ratios (in multiplicative models) of the observed and smoothed series will isolate the seasonal component (plus irregular component). Specifically, the moving average is subtracted from the observed series (for additive models) or the observed series is divided by the moving average values (for multiplicative models).
|
| Сезонная составляющая. На следующем шаге вычисляется сезонная составляющая, как среднее (для аддитивных моделей) или урезанное среднее (для мультипликативных моделей) всех значений ряда, соответствующих данной точке сезонного интервала.
| Seasonal components. The seasonal component is then computed as the average (for additive models) or medial average (for multiplicative models) for each point in the season.
|

| 
|
| Сезонная корректировка ряда. Исходный ряд можно скорректировать, вычитая из него (аддитивная модель) или деля его значения на (мультипликативная модель) значения сезонной составляющей.
|
Seasonally adjusted series. The original series can be adjusted by subtracting from it (additive models) or dividing it by (multiplicative models) the seasonal component.
|
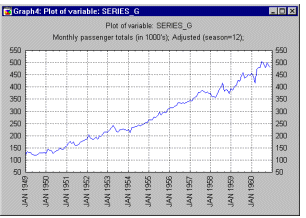
| 
|
| Получающийся в результате ряд называется сезонной корректировкой ряда (из ряда убрана сезонная составляющая)..
| The resulting series is the seasonally adjusted series (i. e., the seasonal component will be removed).
|
| Тренд-циклическая компонента. Напомним, что циклическая компонента отличается от сезонной компоненты тем, что продолжительность цикла, как правило, больше, чем один сезонный период, и разные циклы могут иметь разную продолжительность. Приближение для объединенной тренд-циклической компоненты можно получить, применяя к ряду с сезонной поправкой процедуру 5-точечного (центрированного) взвешенного скользящего среднего с весами 1, 2, 3, 2, 1.
| Trend-cycle component. Remember that the cyclical component is different from the seasonal component in that it is usually longer than one season, and different cycles can be of different lengths. The combined trend and cyclical component can be approximated by applying to the seasonally adjusted series a 5 point (centered) weighed moving average smoothing transformation with the weights of 1, 2, 3, 2, 1.
|
| Случайная или нерегулярная компонента. На последнем шаге выделяется случайная или нерегулярная компонента (погрешность) путем вычитания из ряда с сезонной поправкой (аддитивная модель) или делением этого ряда (мультипликативная модель) на тренд-циклическую компоненту.
| Random or irregular component. Finally, the random or irregular (error) component can be isolated by subtracting from the seasonally adjusted series (additive models) or dividing the adjusted series by (multiplicative models) the trend-cycle component.
|
| Сезонная корректировка X-11 (метод Census II)
| X-11 Census Method II Seasonal Adjustment
|
| Общие идеи, лежащие в основе сезонной декомпозиции и корректировки, изложены в разделе, посвященном методу сезонной корректировки Census I (см. Сезонная декомпозиция (метод Census I)). Метод Census II (2) является развитием и уточнением обычного метода корректировки. На протяжении многих лет различные варианты метода Census II развивались в Бюро Переписи США (US Census Bureau); один из вариантов этого метода, получивший широкую известность и наиболее часто применяемый в государственных органах и сфере бизнеса, называется " вариант X-11 метода Census II" (см. Shiskin, Young, and Musgrave, 1967). Впоследствии этот усовершенствованный вариант метода Census II стал называться просто X-11. Помимо документации, которую можно получить из Census Bureau, подробное описание метода дано в работах Makridakis, Wheelwright and McGee (1983), Makridakis and Wheelwright (1989).
| The general ideas of seasonal decomposition and adjustment are discussed in the context of the Census I seasonal adjustment method (Seasonal Decomposition (Census I)). The Census method II (2) is an extension and refinement of the simple adjustment method. Over the years, different versions of the Census method II evolved at the Census Bureau; the method that has become most popular and is used most widely in government and business is the so-called X-11 variant of the Census method II (see Hiskin, Young, & Musgrave, 1967). Subsequently, the term X-11 has become synonymous with this refined version of the Census method II. In addition to the documentation that can be obtained from the Census Bureau, a detailed summary of this method is also provided in Makridakis, Wheelwright, and McGee (1983) and Makridakis and Wheelwright (1989).
|
| За дополнительной информацией обратитесь к следующим разделам:
| For more information on this method, see the following topics:
|
| • Сезонная корректировка: основные идеи и термины
| Seasonal Adjustment: Basic Ideas and Terms
|
| • Метод Census II
| The Census II Method
|
| • Таблицы результатов корректировки X-11
| Results Tables Computed by the X-11 Method
|
| • Подробное описание всех таблиц результатов, вычисляемых в методе X-11
| - Specific Description of all Results Tables Computed by the X-11 Method
|
| За дальнейшей информацией обратитесь к Анализу временных рядов и следующим разделам:
| - For more information on other Time Series methods, see Time Series Analysis - Index and the following topics:
|
| • Идентификация модели временных рядов
| - Identifying Patterns in Time Series Data
|
| • АРПСС (Бокс и Дженкинс) и автокорреляции
| - ARIMA (Box & Jenkins) and Autocorrelations
|
| • Прерванные временные ряды
| Interrupted Time series
|
| • Экспоненциальное сглаживание
| |
| • Сезонная декомпозиция (метод Census I)
| - Seasonal Decomposition (Census I)
|
| • Анализ распределенных лагов
| - Distributed Lags Analysis
|
| • Одномерный анализ Фурье
| - Single Spectrum (Fourier) Analysis
|
| • Кросс-спектральный анализ
| |
| • Основные понятия и принципы
| - Basic Notations and Principles
|
| • Быстрое преобразование Фурье
| - Fast Fourier Transformations
|
| Сезонная корректировка: основные идеи и термины
| Seasonal Adjustment: Basic Ideas and Terms.
|
| Предположим, что у вас имеются ежемесячные данные о пассажиропотоке на международных авиалиниях за 12 лет (см. Бокс и Дженкинс, 1976). Если изобразить эти данные на графике, то будет хорошо видно, что (1) объем пассажиропотока имеет во времени возрастающий линейный тренд, и что (2) в ряде имеется ежегодно повторяющаяся закономерность - сезонность (большинство перевозок приходится на летние месяцы, кроме того, имеется пик меньшей высоты в районе декабрьских каникул). Цель сезонной декомпозиции и корректировки как раз и состоит в том, чтобы отделить эти компоненты, то есть разложить ряд на составляющую тренда, сезонную компоненту и оставшуюся нерегулярную составляющую. " Классический" прием, позволяющий выполнить такую декомпозицию, известен как метод Census I (см. раздел Census I). Этот метод описывается и обсуждается в работах Makridakis, Wheelwright, and McGee (1983) и Makridakis and Wheelwright (1989).
| Suppose you recorded the monthly passenger load on international flights for a period of 12 years ( see Box & Jenkins, 1976). If you plot those data, it is apparent that (1) there appears to be an upwards linear trend in the passenger loads over the years, and (2) there is a recurring pattern or seasonality within each year (i. e., most travel occurs during the summer months, and a minor peak occurs during the December holidays). The purpose of seasonal decomposition and adjustment is to isolate those components, that is, to de-compose the series into the trend effect, seasonal effects, and remaining variability. The " classic" technique designed to accomplish this decomposition was developed in the 1920's and is also known as the Census I method (see the Census I overview section). This technique is also described and discussed in detail in Makridakis, Wheelwright, and McGee (1983), and Makridakis and Wheelwright (1989).
|
| Общая модель. Основная идея сезонной декомпозиции проста. В общем случае временной ряд типа того, который описан выше, можно представить себе состоящим из четырех различных компонент: (1) сезонной компоненты (обозначается St, где t обозначает момент времени), (2) тренда (Tt), (3) циклической компоненты (Ct) и (4) случайной, нерегулярной компоненты или флуктуации (It). Разница между циклической и сезонной компонентой состоит в том, что последняя имеет регулярную (сезонную) периодичность, тогда как циклические факторы обычно имеют более длительный эффект, который к тому же меняется от цикла к циклу. В методе Census I тренд и циклическую компоненту обычно объединяют в одну тренд-циклическую компоненту (TCt). Конкретные функциональные взаимосвязи между этими компонентами могут иметь самый разный вид. Однако, можно выделить два основных способа, с помощью которых они могут взаимодействовать: аддитивно и мультипликативно:
| General model. The general idea of seasonal decomposition is straightforward. In general, a time series like the one described above can be thought of as consisting of four different components: (1) A seasonal component (denoted as St, where t stands for the particular point in time) (2) a trend component (Tt), (3) a cyclical component (Ct), and (4) a random, error, or irregular component (It). The difference between a cyclical and a seasonal component is that the latter occurs at regular (seasonal) intervals, while cyclical factors usually have a longer duration that varies from cycle to cycle. The trend and cyclical components are customarily combined into a trend-cycle component (TCt). The specific functional relationship between these components can assume different forms. However, two straightforward possibilities are that they combine in an additive or a multiplicative fashion:
|
| Аддитивная модель:
| Additive Model:
|
| Xt = TCt + St + It
| Xt = TCt + St + It
|
| Мультипликативная модель:
| Multiplicative Model:
|
| Xt = Tt*Ct*St*It
| Xt = Tt*Ct*St*It
|
| Здесь Xt обозначает значение временного ряда в момент времени t.
| Where Xt represents the observed value of the time series at time t.
|
| Если имеются какие-то априорные сведения о циклических факторах, влияющих на ряд (например, циклы деловой конъюнктуры), то можно использовать оценки для различных компонент для составления прогноза будущих значений ряда. (Однако для прогнозирования предпочтительнее экспоненциальное сглаживание, позволяющее учитывать сезонную составляющую и тренд. )
| Given some a priori knowledge about the cyclical factors affecting the series (e. g., business cycles), the estimates for the different components can be used to compute forecasts for future observations. (However, the Exponential smoothing method, which can also incorporate seasonality and trend components, is the preferred technique for forecasting purposes. )
|
| Аддитивная и мультипликативная сезонность. Рассмотрим на примере различие между аддитивной и мультипликативной сезонными компонентами. График объема продаж детских игрушек, вероятно, будет иметь ежегодный пик в ноябре-декабре, и другой - существенно меньший по высоте - в летние месяцы, приходящийся на каникулы. Такая сезонная закономерность будет повторяться каждый год. По своей природе сезонная компонента может быть аддитивной или мультипликативной. Так, например, каждый год объем продаж некоторой конкретной игрушки может увеличиваться в декабре на 3 миллиона долларов. Поэтому вы можете учесть эти сезонные изменения, прибавляя к своему прогнозу на декабрь 3 миллиона. Здесь мы имеем аддитивную сезонность. Может получиться иначе. В декабре объем продаж некоторой игрушки может увеличиваться на 40%, то есть умножаться на множитель 1. 4. Это значит, например, что если средний объем продаж этой игрушки невелик, то абсолютное (в денежном выражении) увеличение этого объема в декабре также будет относительно небольшим (но в процентном исчислении оно будет постоянным); если же игрушка продается хорошо, то и абсолютный (в долларах) рост объема продаж будет значительным. Здесь опять, объем продаж возрастает в число раз, равное определенному множителю, а сезонная компонента, по своей природе, мультипликативная компонента (в данном случае равная 1. 4). Если перейти к графикам временных рядов, то различие между этими двумя видами сезонности будет проявляться так: в аддитивном случае ряд будет иметь постоянные сезонные колебания, величина которых не зависит от общего уровня значений ряда; в мультипликативном случае величина сезонных колебаний будет меняться в зависимости от общего уровня значений ряда.
| Additive and multiplicative seasonality. Consider the difference between an additive and multiplicative seasonal component in an example: The annual sales of toys will probably peak in the months of November and December, and perhaps during the summer (with a much smaller peak) when children are on their summer break. This seasonal pattern will likely repeat every year. Seasonal components can be additive or multiplicative in nature. For example, during the month of December the sales for a particular toy may increase by 3 million dollars every year. Thus, you could add to your forecasts for every December the amount of 3 million to account for this seasonal fluctuation. In this case, the seasonality is additive. Alternatively, during the month of December the sales for a particular toy may increase by 40%, that is, increase by a factor of 1. 4. Thus, when the sales for the toy are generally weak, then the absolute (dollar) increase in sales during December will be relatively weak (but the percentage will be constant); if the sales of the toy are strong, then the absolute (dollar) increase in sales will be proportionately greater. Again, in this case the sales increase by a certain factor, and the seasonal component is thus multiplicative in nature (i. e., the multiplicative seasonal component in this case would be 1. 4). In plots of series, the distinguishing characteristic between these two types of seasonal components is that in the additive case, the series shows steady seasonal fluctuations, regardless of the overall level of the series; in the multiplicative case, the size of the seasonal fluctuations vary, depending on the overall level of the series.
|
| Аддитивный и мультипликативный тренд-цикл. Рассмотренный пример можно расширить, чтобы проиллюстрировать понятия аддитивной и мультипликативной тренд-циклических компонент. В случае с игрушками, тренд " моды" может привести к устойчивому росту продаж (например, это может быть общий тренд в сторону игрушек образовательной направленности). Как и сезонная компонента, этот тренд может быть по своей природе аддитивным (продажи ежегодно увеличиваются на 3 миллиона долларов) или мультипликативным (продажи ежегодно увеличиваются на 30%, или возрастают в 1. 3 раза). Кроме того, объем продаж может содержать циклические компоненты. Повторим еще раз, что циклическая компонента отличается от сезонной тем, что она обычно имеет большую временную протяженность и проявляется через неравные промежутки времени. Так, например, некоторая игрушка может быть особенно " горячей" в течение летнего сезона (например, кукла, изображающая персонаж популярного мультфильма, которая к тому же агрессивно рекламируется). Как и в предыдущих случаях, такая циклическая компонента может изменять объем продаж аддитивно, либо мультипликативно.
| Additive and multiplicative trend-cycle. The previous example can be extended to illustrate the additive and multiplicative trend-cycle components. In terms of the toy example, a " fashion" trend may produce a steady increase in sales (e. g., a trend towards more educational toys in general); as with the seasonal component, this trend may be additive (sales increase by 3 million dollars per year) or multiplicative (sales increase by 30%, or by a factor of 1. 3, annually) in nature. In addition, cyclical components may impact sales. To reiterate, a cyclical component is different from a seasonal component in that it usually is of longer duration, and that it occurs at irregular intervals. For example, a particular toy may be particularly " hot" during a summer season (e. g., a particular doll which is tied to the release of a major children's movie, and is promoted with extensive advertising). Again such a cyclical component can effect sales in an additive manner or multiplicative manner.
|
|
|
|
| Метод Census II
| The Census II Method
|
| Основной метод сезонной декомпозиции и корректировки, рассмотренный в разделе Сезонная корректировка: основные идеи и термины, может быть усовершенствован различными способами. На самом деле, в отличие от многих методов моделирования временных рядов (в частности, АРПСС), которые основаны на определенной теоретической модели, вариант X-11 метода Census II представляет собой просто результат многочисленных специально разработанных приемов и усовершенствований, которые доказали свою работоспособность в многолетней практике решения реальных задач (см. Burman, 1979, Kendall and Ord, 1990, Makridakis and Wheelwright, 1989; Wallis, 1974). Некоторые из наиболее важных усовершенствований перечислены ниже.
| The basic method for seasonal decomposition and adjustment outlined in the Basic Ideas and Terms topic can be refined in several ways. In fact, unlike many other time-series modeling techniques (e. g., ARIMA) which are grounded in some theoretical model of an underlying process, the X-11 variant of the Census II method simply contains many ad hoc features and refinements, that over the years have proven to provide excellent estimates for many real-world applications (see Burman, 1979, Kendal & Ord, 1990, Makridakis & Wheelwright, 1989; Wallis, 1974). Some of the major refinements are listed below.
|
| Поправка на число рабочих дней. В месяцах разное число дней и разное число рабочих дней. Если мы анализируем, например, цифры ежемесячной выручки парка аттракционов, то разница в числе суббот и воскресений (пиковые дни) в разных месяцах существенным образом скажется на различиях в ежемесячных показателях дохода. Вариант X-11 метода Census II дает пользователю возможность проверить, присутствует ли во временном ряду этот эффект числа рабочих дней, и если да, то внести соответствующие поправки.
| Trading-day adjustment. Different months have different numbers of days, and different numbers of trading-days (i. e., Mondays, Tuesdays, etc. ). When analyzing, for example, monthly revenue figures for an amusement park, the fluctuation in the different numbers of Saturdays and Sundays (peak days) in the different months will surely contribute significantly to the variability in monthly revenues. The X-11 variant of the Census II method allows the user to test whether such trading-day variability exists in the series, and, if so, to adjust the series accordingly.
|
| Выбросы. Большинство реальных временных рядов содержит выбросы, то есть резко выделяющиеся наблюдения, вызванные какими-то исключительными событиями. Например, забастовка персонала может сильно повлиять на месячные или годовые показатели выпуска продукции фирмы. Такие выбросы могут исказить оценки сезонной компоненты и тренда. В процедуре X-11 предусмотрены корректировки на случай появления выбросов, основанные на использовании " принципов статистического контроля": значения, выходящие за определенный диапазон (который определяется в терминах, кратных сигма, т. е. стандартных отклонений), могут быть преобразованы или вовсе пропущены, и только после этого будут вычисляться окончательные оценки параметров сезонности.
| Extreme values. Most real-world time series contain outliers, that is, extreme fluctuations due to rare events. For example, a strike may affect production in a particular month of one year. Such extreme outliers may bias the estimates of the seasonal and trend components. The X-11 procedure includes provisions to deal with extreme values through the use of " statistical control principles, " that is, values that are above or below a certain range (expressed in terms of multiples of sigma, the standard deviation) can be modified or dropped before final estimates for the seasonality are computed.
|
| Последовательные уточнения. Корректировки, связанные с наличием выбросов и различным числом рабочих дней можно производить многократно, чтобы последовательно получать для компонент оценки все лучшего качества. В методе X-11 делается несколько последовательных уточнений оценок для получения окончательных компонент тренд-цикличности и сезонности, нерегулярной составляющей, и самого временного ряда с сезонными поправками.
| Multiple refinements. The refinement for outliers, extreme values, and different numbers of trading-days can be applied more than once, in order to obtain successively improved estimates of the components. The X-11 method applies a series of successive refinements of the estimates to arrive at the final trend-cycle, seasonal, and irregular components, and the seasonally adjusted series.
|
| Критерии и итоговые статистики. Помимо оценки основных компонент ряда, можно вычислить различные сводные статистики. Например, можно сформировать таблицы дисперсионного анализа для проверки значимости фактора сезонной изменчивости и ряда и фактора рабочих дней (см. выше), процедура метода X-11 вычисляет также ежемесячные относительные изменения в случайной и тренд-циклической компонентах. С увеличением продолжительности временного промежутка, измеряемого в месяцах или, в случае квартального варианта метода X-11 - в кварталах года, изменения в тренд-циклической компоненте, вообще говоря, будут нарастать, в то время как изменения случайной составляющей должны оставаться примерно на одном уровне. Средняя длина временного интервала, на котором изменения тренд-циклической компоненты становятся примерно равными изменениям случайной компоненты, называется месяцем (кварталом) циклического доминирования, или сокращенно МЦД (соответственно КЦД). Например, если МЦД равно двум, то на сроках более двух месяцев тренд-циклическая компонента станет доминировать над флуктуациями нерегулярной (случайной) компоненты. Эти и другие результаты более подробно будут обсуждаться далее.
| Tests and summary statistics. In addition to estimating the major components of the series, various summary statistics can be computed. For example, analysis of variance tables can be prepared to test the significance of seasonal variability and trading-day variability (see above) in the series; the X-11 procedure will also compute the percentage change from month to month in the random and trend-cycle components. As the duration or span in terms of months (or quarters for quarterly X-11) increases, the change in the trend-cycle component will likely also increase, while the change in the random component should remain about the same. The width of the average span at which the changes in the random component are about equal to the changes in the trend-cycle component is called the month (quarter) for cyclical dominance, or MCD (QCD) for short. For example, if the MCD is equal to 2 then one can infer that over a 2 month span the trend-cycle will dominate the fluctuations of the irregular (random) component. These and various other results are discussed in greater detail below.
|
|
|
|
| Таблицы результатов корректировки X-11
| Result Tables Computed by the X-11 Method
|
| Вычисления, которые производятся в процедуре X-11, лучше всего обсуждать в контексте таблиц результатов, которые при этом выдаются. Процедура корректировки разбивается на семь этапов, которые обычно обозначаются буквами A - G.
| The computations performed by the X-11 procedure are best discussed in the context of the results tables that are reported. The adjustment process is divided into seven major steps, which are customarily labeled with consecutive letters A through G.
|
| Априорная корректировка (помесячная сезонная корректировка). Перед тем, как к временному ряду, содержащему ежемесячные значения, будет применяться какая-либо сезонная корректировка, могут быть произведены различные корректировки, заданные пользователем. Можно ввести еще один временной ряд, содержащий априорные корректирующие факторы; значения этого ряда будут вычитаться из исходного ряда (аддитивная модель), или же значения исходного ряда будут поделены на значения корректирующего ряда (мультипликативная модель). В случае мультипликативной модели пользователь может также определить свои собственные поправочные коэффициенты (веса) на число рабочих дней. Эти веса будут использоваться для корректировки ежемесячных наблюдений, так чтобы учитывалось число рабочих дней в этом месяце.
| Prior adjustment (monthly seasonal adjustment only). Before any seasonal adjustment is performed on the monthly time series, various prior user- defined adjustments can be incorporated. The user can specify a second series that contains prior adjustment factors; the values in that series will either be subtracted (additive model) from the original series, or the original series will be divided by these values (multiplicative model). For multiplicative models, user-specified trading-day adjustment weights can also be specified. These weights will be used to adjust the monthly observations depending on the number of respective trading-days represented by the observation.
|
| Предварительное оценивание вариации числа рабочих дней (месячный вариант X-11) и весов. На следующем шаге вычисляются предварительные поправочные коэффициенты на число рабочих дней (только в месячном варианте X-11) и веса, позволяющие уменьшить эффект выбросов.
| Preliminary estimation of trading-day variation (monthly X-11) and weights. Next, preliminary trading-day adjustment factors (monthly X-11 only) and weights for reducing the effect of extreme observations are computed.
|
| Окончательное оценивание вариации числа рабочих дней и нерегулярных весов (месячный вариант X-11). Поправки и веса, вычисленные в пункте B, используются для построения улучшенных оценок тренд-циклической и сезонной компонент. Эти улучшенные оценки используются для окончательного вычисления факторов числа рабочих дней (в месячном варианте X-11) и весов.
| Final estimation of trading-day variation and irregular weights (monthly X- 11). The adjustments and weights computed in B above are then used to derive improved trend-cycle and seasonal estimates. These improved estimates are used to compute the final trading-day factors (monthly X-11 only) and weights.
|
| Окончательное оценивание сезонных факторов, тренд-циклической, нерегулярной и сезонно скорректированной компонент ряда. Окончательные значения факторов рабочих дней и весов, вычисленные в пункте C, используются для вычисления окончательных оценок для компонент ряда.
| Final estimation of seasonal factors, trend-cycle, irregular, and seasonally adjusted series. The final trading-day factors and weights computed in C above are used to compute the final estimates of the components.
|
| Модифицированные ряды: исходный, сезонно скорректированный и нерегулярный. Исходный и окончательный сезонно скорректированный ряды, а также нерегулярная компонента модифицируются путем сглаживания выбросов. Полученные в результате этого, модифицированные ряды позволяют пользователю проверить устойчивость сезонной корректировки.
| Modified original, seasonally adjusted, and irregular series. The original and final seasonally adjusted series, and the irregular component are modified for extremes. The resulting modified series allow the user to examine the stability of the seasonal adjustment.
|
| Месяц (квартал) циклического доминирования (МЦД, КЦД), скользящее среднее и сводные показатели. IНа этом этапе вычислений рассчитываются различные сводные характеристики (см. далее), позволяющие пользователю исследовать относительную важность разных компонент, среднюю флуктуацию от месяца к месяцу (от квартала к кварталу), среднее число идущих подряд изменений в одну сторону и др.
| Month (quarter) for cyclical dominance (MCD, QCD), moving average, and summary measures. In this part of the computations, various summary measures (see below) are computed to allow the user to examine the relative importance of the different components, the average fluctuation from month-to-month (quarter-to-quarter), the average number of consecutive changes in the same direction (average number of runs), etc.
|
| Графики. Наконец, вы можете построить различные графики итоговых результатов. Например, можно построить окончательно скорректированный ряд в хронологическом порядке или по месяцам (см. ниже).
| Charts. Finally, you will compute various charts (graphs) to summarize the results. For example, the final seasonally adjusted series will be plotted, in chronological order, or by month (see below).
|
|
|
|
| Подробное описание всех таблиц результатов, вычисляемых в методе X-11
| Specific Description of all Result Tables Computed by the X-11 Method
|
| На каждом из этапов A - G (см. раздел Таблицы результатов корректировки X-11) вычислялись различные таблицы результатов. Обычно все они нумеруются, а также им приписывается буква, соответствующая этапу анализа. Например, таблица B 11 содержит предварительно сезонно скорректированный ряд; C 11 - это более точно сезонно скорректированный ряд, а D 11 - окончательный сезонно скорректированный ряд. Далее приводится перечень всех таблиц. Таблицы, помеченные звездочкой (*), недоступны (или неприменимы) при анализе квартальных показателей. Кроме того, в случае квартальной корректировки некоторые из описанных ниже вычислений несколько видоизменяются. Так, например, для вычисления сезонных факторов вместо 12-периодного (т. е. 12-месячного) скользящего среднего используется 4-периодное (4-квартальное) скользящее среднее; предварительная тренд-циклическая компонента вычисляется по центрированному 4-периодному скользящему среднему, а окончательная оценка тренд-циклической компоненты вычисляется по 5-точечному среднему Хендерсона.
| In each part A through G of the analysis (see Results Tables Computed by the X-11 Method), different result tables are computed. Customarily, these tables are numbered, and also identified by a letter to indicate the respective part of the analysis. For example, table B 11 shows the initial seasonally adjusted series; C 11 is the refined seasonally adjusted series, and D 11 is the final seasonally adjusted series. Shown below is a list of all available tables. Those tables identified by an asterisk (*) are not available (applicable) when analyzing quarterly series. (Also, for quarterly adjustment, some of the computations outlined below are slightly different; for example instead of a 12-term [monthly] moving average, a 4-term [quarterly] moving average is applied to compute the seasonal factors; the initial trend-cycle estimate is computed via a centered 4-term moving average, the final trend-cycle estimate in each part is computed by a 5-term Henderson average. )
|
| В соответствии со стандартом метода X-11, принятым Бюро переписи США, предусмотрены три степени подробности вывода: Стандартный (17 - 27 таблиц), Длинный (27 - 39 таблиц) и Полный (44 - 59 таблиц). Имеется также возможность выводить только таблицы результатов, выбранные пользователем. В следующих далее описаниях таблиц, буквы С, Д и П рядом с названием таблицы указывают, какие таблицы выводятся и/или распечатываются в соответствующем варианте вывода. (Для графиков предусмотрены два уровня подробности вывода: Стандартный и Все. )
| Following the convention of the Bureau of the Census version of the X-11 method, three levels of printout detail are offered: Standard (17 to 27 tables), Long (27 to 39 tables), and Full (44 to 59 tables). In the description of each table below, the letters S, L, and F are used next to each title to indicate, which tables will be displayed and/or printed at the respective setting of the output option. (For the charts, two levels of detail are available: Standard and All. )
|
| Щелкните на имени таблицы для получения информации о ней.
| See the table name below, to obtain more information about that table.
|
| * A 1. Исходный ряд (С)
| |
| | * A 2. Априорные месячные поправки (С)
| |
| | * A 3. Исходный ряд, скорректированный с помощью априорных месячных поправок (С)
| |
| | * A 4. Априорные поправки на рабочие дни (С)
| |
| | B 1. Ряд после априорной корректировки либо исходный ряд (С)
| |
| | B 2. Тренд-цикл (Д)
| |
| | B 3. Немодифицированные S-I разности или отношения (П)
| |
| | B 4. Значения для замены выбросов S-I разностей (отношений) (П)
| |
| | B 5. Сезонная составляющая (П)
| |
| | B 6. Сезонная корректировка ряда (П)
| |
| | B 7. Тренд-цикл (Д)
| |
| | B 8. Немодифицированные S-I разности (отношения) (П)
| |
| | B 9. Значения для замены выбросов S-I разностей (отношений) (П)
| |
| | B 10. Сезонная составляющая (Д)
| |
| | B 11. Сезонная корректировка ряда (П)
| |
| | B 12. (не используется)
| | B 13. Нерегулярная составляющая ряда (Д)
| |
| | Таблицы B 14 - B 16, B 18 и B 19: Поправка на число рабочих дней. Эти таблицы доступны только при анализе ежемесячных данных. Число разных дней недели (понедельников, вторников и т. д. ) колеблется от месяца к месяцу. Бывают ряды, в которых различия в числе рабочих дней в месяце могут давать заметный разброс ежемесячных показателей (например, месячный доход парка аттракционов сильно зависит от того, сколько в этом месяце было выходных дней). Пользователь имеет возможность определить начальные веса для каждого дня недели (см. A 4), и/или эти веса могут быть оценены по данным (пользователь также может сделать использование этих весов условным, т. е. только в тех случаях, когда они объясняют значительную часть дисперсии).
| | * B 14. Выбросы нерегулярной составляющей, исключенные из регрессии рабочих дней (Д)
| |
| | * B 15. Предварительная регрессия рабочих дней (Д)
| |
| | * B 16. Поправки на число рабочих дней, полученные из коэффициентов регрессии (П)
| |
| | B 17. Предварительные веса нерегулярной компоненты (Д)
| |
| | * B 18. Поправки на число рабочих дней, полученные из комбинированных весов дней недели (П)
| |
| | * B 19. Исходный ряд с поправками на рабочие дни и априорную вариацию (П)
| |
| | C 1. Исходный ряд, модифицированный с помощью предварительных весов, с поправкой на рабочие дни и априорную вариацию (Д)
| |
| | C 2. Тренд-цикл (П)
| |
| | C 3. (не используется)
| | C 4. Модифицированные S-I разности (отношения) (П)
| |
| | C 5. Сезонная составляющая (П)
| |
| | C 6. Сезонная корректировка ряда (П)
| |
| | C 7. Тренд-цикл (Д)
| |
| | C 8. (не используется)
| | C 9. Модифицированные S-I разности (отношения) (П)
| |
| | C 10. Сезонная составляющая (Д)
| |
| | C 11. Сезонная корректировка ряда (П)
| |
| | C 12. (не используется)
| | C 13. Нерегулярная составляющая (С)
| |
| | Таблицы C 14 - C 16, C 18 и C 19: Поправка на число рабочих дней. Эти таблицы доступны только при анализе ежемесячных данных и если при этом требуется поправка на различное число рабочих дней. В этом случае поправки на число рабочих дней вычисляются по уточненным значениям сезонно скорректированных рядов аналогично тому, как это делалось в пункте B (B 14 - B 16, B 18, B 19).
| | * C 14. Выбросы нерегулярной составляющей, исключенные из регрессии рабочих дней (С)
| |
| | * C 15. Регрессия рабочих дней - окончательный вариант (С)
| |
| | * C 16. Поправки на число рабочих дней, полученные из коэффициентов регрессии, - окончательный вариант (С)
| |
| | C 17. Окончательные веса нерегулярной компоненты (С)
| |
| | * C 18. Поправки на число рабочих дней, полученные из комбинированных весов дней недели - окончательный вариант (С)
| |
| | * C 19. Исходный ряд с поправками на рабочие дни и априорную вариацию (С)
| |
| | D 1. Исходный ряд, модифицированный с помощью окончательных весов, с поправкой на рабочие дни и априорную вариацию (Д)
| |
| | D 2. Тренд-цикл (П)
| |
| | D 3. (не используется)
| | D 4. Модифицированные S-I разности (отношения) (П)
| |
| | D 5. Сезонная составляющая (П)
| |
| | D 6. Сезонная корректировка ряда (П)
| |
| | D 7. Тренд-цикл (Д)
| |
| | D 8. Немодифицированные S-I разности (отношения) - окончательный вариант (С)
| |
| | D 9. Окончательные значения для замены выбросов S-I разностей (отношений) (С)
| |
| | D 10. Сезонная составляющая - окончательный вариант (С)
| |
| | D 11. Сезонная корректировка ряда - окончательный вариант (С)
| |
| | D 12. Тренд-циклическая компонента - окончательный вариант (С)
| |
| | D 13. Нерегулярная составляющая - окончательный вариант (С)
| |
| | E 1. Модифицированный исходный ряд (С)
| |
| | E 2. Модифицированный ряд с сезонной поправкой (С)
| |
| | E 3. Модифицированная нерегулярная составляющая (С)
| |
| | E 4. Разности (отношения) годовых сумм (С)
| |
| | E 5. Разности (относительные изменения) исходного ряда (С)
| |
| | E 6. Разности (относительные изменения) окончательного варианта ряда с сезонной поправкой (С)
| |
| | F 1. МЦД (КЦД) скользящее среднее (С)
| |
| | F 2. Сводные показатели (С)
| |
| | G 1. График (С)
| |
| | G 2. График (С)
| |
| | G 3. График (В)
| |
| | G 4. График (В)
| |
|
| | *A 1. Original Series(S)
| |
| | * A 2. Prior Monthly Adjustment (S)Factors
| |
| | * A 3. Original Series Adjusted by Prior Monthly Adjustment Factors(S)
| |
| | * A 4. Prior Trading Day Adjustment Factors(S)
| |
| | B 1. Prior Adjusted Series or Original Series(S)
| |
| | B 2. Trend-cycle (L )
| |
| | B 3. Unmodified S-I Differences or Ratios(F)
| |
| | B 4. Replacement Values for Extreme S-I Differences (Ratios)(F)
| |
| | B 5. Seasonal Factors(F)
| |
| | B 6. Seasonally Adjusted Series(F)
| |
| | B 7. Trend-cycle(L)
| |
| | B 8. Unmodified S-I Differences (Ratios)(F)
| |
| | B 9. Replacement Values for Extreme S-I Differences (Ratios)(F)
| |
| | B 10. Seasonal Factors(L)
| |
| | B 11. Seasonally Adjusted Series(F)
| |
| | B 12. (not used)
| | B 13. Irregular Series (L)
| |
| | Tables B 14 through B 16, B18, and B19: Adjustment for trading-day variation. These tables are only available when analyzing monthly series. Different months contain different numbers of days of the week (i. e., Mondays, Tuesdays, etc. ). In some series, the variation in the different numbers of trading-days may contribute significantly to monthly fluctuations (e. g., the monthly revenues of an amusement park will be greatly influenced by the number of Saturdays/Sundays in each month). The user can specify initial weights for each trading-day (see A 4), and/or these weights can be estimated from the data (the user can also choose to apply those weights conditionally, i. e., only if they explain a significant proportion of variance).
| | * B 14. Extreme Irregular Values Excluded from Trading-day Regression (L)
| |
| | * B 15. Preliminary Trading-day Regression (L)
| |
| | * B 16. Trading-day Adjustment Factors Derived from Regression Coefficients (F)
| |
| | B 17. Preliminary Weights for Irregular Component(L)
| |
| | * B 18. Trading-day Factors Derived from Combined Daily Weights (F)
| |
| | * B 19. Original Series Adjusted for Trading-day and Prior Variation(F)
| |
| | C 1. Original Series Modified by Preliminary Weights and Adjusted for Trading-day and Prior Variation (L)
| |
| | C 2. Trend-cycle (F)
| |
| | C 3. (not used)
| | C 4. Modified S-I Differences (Ratios) (F)
| |
| | C 5. Seasonal Factors(F)
| |
| | C 6. Seasonally Adjusted Series(F)
| |
| | C 7. Trend-cycle(L)
| |
| | C 8. (not used)
| | C 9. Modified S-I Differences (Ratios)(F
| |
| | C 10. Seasonal Factors (L)
| |
| | C 11. Seasonally Adjusted Series (F>
| |
| | C 12. (not used)
| | C 13. Irregular Series (S)
| |
| | Tables C 14 through C 16, C 18, and C 19: Adjustment for trading-day variation. These tables are only available when analyzing monthly series, and when adjustment for trading-day variation is requested. In that case, the trading-day adjustment factors are computed from the refined adjusted series, analogous to the adjustment performed in part B (B 14 through B 16, B 18 and B 19).
| | * C 14. Extreme Irregular Values Excluded from Trading-day Regression (S)
| |
| | * C 15. Final Trading-day Regression (S)
| |
| | * C 16. Final Trading-day Adjustment Factors Derived from Regression X11 output: Coefficients (S)
| |
| | C 17. Final Weights for Irregular Component (S)
| |
| | * C 18. Final Trading-day Factors Derived From Combined Daily Weights (S)
| |
| | * C 19. Original Series Adjusted for Trading-day and Prior Variation (S)
| |
| | D 1. Original Series Modified by Final Weights and Adjusted for Trading-day and Prior Variation (L)
| |
| | D 2. Trend-cycle
| |
| | D 3. (not used)
| | D 4. Modified S-I Differences (Ratios) (F)
| |
| | D 5. Seasonal Factors (F)
| |
| | D 6. Seasonally Adjusted Series (F)
| |
| | D 7. Trend-cycle (L)
| |
| | D 8. Final Unmodified S-I Differences (Ratios) (S)
| |
| | D 9. Final Replacement Values for Extreme S-I Differences (Ratios) (S)
| |
| | D 10. Final Seasonal Factors (S)
| |
| | D 11. Final Seasonally Adjusted Series (S)
| |
| | D 12. Final Trend-cycle (S)
| |
| | D 13. Final Irregular (S)
| |
| | E 1. Modified Original Series (S)
| |
| | E 2. Modified Seasonally Adjusted Series (S)
| |
| | E 3. Modified Irregular Series (S)
| |
| | E 4. Differences (Ratios) of Annual Totals (S)
| |
| | E 5. Differences (Percent Changes) in Original Series (S)
| |
| | E 6. Differences (Percent Changes) in Final Seasonally Adjusted Series (S)
| |
| | F 1. MCD (QCD) Moving Average (S)
| |
| | F 2. Summary Measures (S)
| |
| | G 1. Chart (S)
| |
| | G 2. Chart (S)
| |
| | G 3. Chart (A)
| |
| | G 4. Chart (A)
| |
|
|
| Анализ распределенных лагов
| Distributed Lags Analysis Introductory Overview
|
| • Общая цель
| General Purpose
|
| A. • Общая модель
| A. General Model
|
| B. • Распределенный лаг Алмона
| B. Almon Distributed Lag
|
| C. За дальнейшей информацией обратитесь к Анализу временных рядов и следующим разделам:
| C. For more information on other Time Series methods, see Time Series Analysis - Index and the following topics:
|
| D. • Идентификация модели временных рядов
| D. Identifying Patterns in Time Series Data
|
| E. • АРПСС (Бокс и Дженкинс) и автокорреляции Вводный обзор АРПСС
| E. ARIMA (Box & Jenkins) and Autocorrelations ARIMA Introductory Overview
|
| F. • Прерванные временные ряды
| F. Interrupted Time Series
|
| G. • Экспоненциальное сглаживание
| G. Exponential Smoothing
|
| • Сезонная декомпозиция (метод Census I)
| - Seasonal Decomposition (Census I)
|
| • Сезонная корректировка X-11 (метод Census II)
| - X-11 Census method II seasonal adjustment
|
| • Таблицы результатов корректировки X-11
| - X-11 Census method II result tables
|
| • Одномерный анализ Фурье
| - Single Spectrum (Fourier) Analysis
|
| • Кросс-спектральный анализ
| |
| • Основные понятия и принципы
| - Basic Notations and Principles
|
| • Быстрое преобразование Фурье
| - Fast Fourier Transformations
|
| Общая цель
| General Purpose
|
| Анализ распределенных лагов - это специальный метод оценки запаздывающей зависимости между рядами. Например, предположим, вы производите компьютерные программы и хотите установить зависимость между числом запросов, поступивших от покупателей, и числом реальных заказов. Вы могли бы записывать эти данные ежемесячно в течение года и затем рассмотреть зависимость между двумя переменными: число запросов и число заказов зависит от запросов, но зависит с запаздыванием. Однако очевидно, что запросы предшествуют заказам, поэтому можно ожидать, что число заказов. Иными словами, в зависимости между числом запросов и числом продаж имеется временной сдвиг (лаг) (см. также автокорреляции и кросскорреляции).
| Distributed lags analysis is a specialized technique for examining the relationships between variables that involve some delay. For example, suppose that you are a manufacturer of computer software, and you want to determine the relationship between the number of inquiries that are received, and the number of orders that are placed by your customers. You could record those numbers monthly for a one year period, and then correlate the two variables. However, obviously inquiries will precede actual orders, and one can expect that the number of orders will follow the number of inquiries with some delay. Put another way, there will be a (time) lagged correlation between the number of inquiries and the number of orders that are received.
|
| Такого рода зависимости с запаздыванием особенно часто возникают в эконометрике. Например, доход от инвестиций в новое оборудование отчетливо проявится не сразу, а только через определенное время. Более высокий доход изменяет выбор жилья людьми; однако эта зависимость, очевидно, тоже проявляется с запаздыванием. [Подобные задачи возникают в страховании, где временной ряд клиентов и ряд денежных поступлений сдвинуты друг относительно друга].
| Time-lagged correlations are particularly common in econometrics. For example, the benefits of investments in new machinery usually only become evident after some time. Higher income will change people's choice of rental apartments, however, this relationship will be lagged because it will take some time for people to terminate their current leases, find new apartments, and move. In general, the relationship between capital appropriations and capital expenditures will be lagged, because it will require some time before investment decisions are actually acted upon.
|
| Во всех этих случаях, имеется независимая или объясняющая переменная, которая воздействует на зависимые переменные с некоторым запаздыванием (лагом). Метод распределенных лагов позволяет исследовать такого рода зависимость.
| In all of these cases, we have an independent or explanatory variable that affects the dependent variables with some lag. The distributed lags method allows you to investigate those lags.
|
| Подробные обсуждения зависимостей с распределенными лагами имеются в эконометрических учебниках, например, в Judge, Griffith, Hill, Luetkepohl, and Lee (1985), Maddala (1977), and Fomby, Hill, and Johnson (1984). Ниже дается краткое описание этих методов. Предполагается, что вы знакомы с понятием корреляции (см. Основные статистики и таблицы), кросскорреляции и основными идеями множественной регрессии (см. Множественная регрессия).
| Detailed discussions of distributed lags correlation can be found in most econometrics textbooks, for example, in Judge, Griffith, Hill, Luetkepohl, and Lee (1985), Maddala (1977), and Fomby, Hill, and Johnson (1984). In the following paragraphs we will present a brief description of these methods. We will assume that you are familiar with the concept of correlation (see Basic Statistics), and the basic ideas of multiple regression (see Multiple Regression).
|
| Общая модель
| General Model
|
| Пусть y - зависимая переменная, a независимая или объясняющая x. Эти переменные измеряются несколько раз в течение определенного отрезка времени. В некоторых учебниках по эконометрике зависимая переменная называется также эндогенной переменной, a зависимая или объясняемая переменная экзогенной переменной. Простейший способ описать зависимость между этими двумя переменными дает следующее линейное уравнение:
| Suppose we have a dependent variable y and an independent or explanatory variable x which are both measured repeatedly over time. In some textbooks, the dependent variable is also referred to as the endogenous variable, and the independent or explanatory variable the exogenous variable. The simplest way to describe the relationship between the two would be in a simple linear relationship:
|
| Yt=Σ β i*xt-1
| Yt=Σ β i*xt-1
|
| В этом уравнении значение зависимой переменной в момент времени t является линейной функцией переменной x, измеренной в моменты t, t-1, t-2 и т. д. Таким образом, зависимая переменная представляет собой линейные функции x и x, сдвинутых на 1, 2, и т. д. временные периоды. Бета коэффициенты (β i) могут рассматриваться как параметры наклона в этом уравнении. Будем рассматривать это уравнение как специальный случай уравнения линейной регрессии (см. раздел Множественная регрессия). Если коэффициент переменной с определенным запаздыванием (лагом) значим, то можно заключить, что переменная y предсказывается (или объясняется) с запаздыванием.
| In this equation, the value of the dependent variable at time t is expressed as a linear function of x measured at times t, t-1, t-2, etc. Thus, the dependent variable is a linear function of x, and x is lagged by 1, 2, etc. time periods. The beta weights (bi) can be considered slope parameters in this equation. You may recognize this equation as a special case of the general linear regression equation (see the Multiple Regressionoverview). If the weights for the lagged time periods are statistically significant, we can conclude that the y variable is predicted (or explained) with the respective lag.
|
| Распределенный лаг Алмона
| Almon Distributed Lag
|
| Обычная проблема, возникающая в множественной регрессии, состоит в том, что соседние значения x сильно коррелируют. В самом крайнем случае, это приводит к тому, что корреляционная матрица не будет обратимой и коэффициенты бета не могут быть вычислены. В менее экстремальных ситуациях вычисления этих коэффициентов и их стандартные ошибки становятся ненадежными из-за вычислительных ошибок (ошибок округления). В контексте множественной регрессии эта проблема хорошо известна как проблема мультиколлинеарности (см. раздел Множественная регрессия). Алмон (1965) предложил специальную процедуру, которая в данном случае уменьшает мультиколлинеарность. Именно, пусть каждый неизвестный коэффициент записан в виде:
| A common problem that often arises when computing the weights for the multiple linear regression model shown above is that the values of adjacent (in time) values in the x variable are highly correlated. In extreme cases, their independent contributions to the prediction of y may become so redundant that the correlation matrix of measures can no longer be inverted, and thus, the beta weights cannot be computed. In less extreme cases, the computation of the beta weights and their standard errors can become very imprecise, due to round-off error. In the context of Multiple Regression this general computational problem is discussed as the multicollinearity or matrix ill-conditioning issue.
|
| β i=α 0+α 1*i+…+α q*iq
| β i=α 0+α 1*i+…+α q*iq
|
| Алмон показал, что во многих случаях (в частности, чтобы избежать мультиколлинеарности) легче оценить коэффициенты альфа, чем непосредственно коэффициенты бета. Такой метод оценивания коэффициентов бета называется полиномиальной аппроксимацией.
| Almon could show that in many cases it is easier (i. e., it avoids the multicollinearity problem) to estimate the alpha values than the beta weights directly. Note that with this method, the precision of the beta weight estimates is dependent on the degree or order of the polynomial approximation.
|
| Неправильная спецификация. Общая проблема полиномиальной аппроксимации, состоит в том, что длина лага и степень полинома неизвестны заранее. Последствия неправильного определения (спецификации) этих параметров потенциально серьезны (в силу смещения, возникающего в оценках при неправильном задании параметров). Этот вопрос подробно обсуждается в книгах Frost (1975), Schmidt and Waud (1973), Schmidt and Sickles (1975) и Trivedi and Pagan (1979).
| Misspecifications. A general problem with this technique is that, of course, the lag length and correct polynomial degree are not known a priori. The effects of misspecifications of these parameters are potentially serious (in terms of biased estimation). This issue is discussed in greater detail in Frost (1975), Schmidt and Waud (1973), Schmidt and Sickles (1975), and Trivedi and Pagan (1979).
|
|
|
|
| Одномерный анализ Фурье
| Single Spectrum (Fourier) Analysis
|
| В спектральном анализе исследуются периодические модели данных. Цель анализа - разложить комплексные временные ряды с циклическими компонентами на несколько основных синусоидальных функций с определенной длиной волн. Термин " спектральный" - своеобразная метафора для описания природы этого анализа. Предположим, вы изучаете луч белого солнечного света, который, на первый взгляд, кажется хаотически составленным из света с различными длинами волн. Однако, пропуская его через призму, вы можете отделить волны разной длины или периодов, которые составляют белый свет. Фактически, применяя этот метод, вы можете теперь распознавать и различать разные источники света. Таким образом, распознавая существенные основные периодические компоненты, вы узнали что-то об интересующем вас явлении. В сущности, применение спектрального анализа к временным рядам подобно пропусканию света через призму. В результате успешного анализа можно обнаружить всего несколько повторяющихся циклов различной длины в интересующих вас временных рядах, которые, на первый взгляд, выглядят как случайный шум.
| Spectrum analysis is concerned with the exploration of cyclical patterns of data. The purpose of the analysis is to decompose a complex time series with cyclical components into a few underlying sinusoidal (sine and cosine) functions of particular wavelengths. The term " spectrum" provides an appropriate metaphor for the nature of this analysis: Suppose you study a beam of white sun light, which at first looks like a random (white noise) accumulation of light of different wavelengths. However, when put through a prism, we can separate the different wave lengths or cyclical components that make up white sun light. In fact, via this technique we can now identify and distinguish between different sources of light. Thus, by identifying the important underlying cyclical components, we have learned something about the phenomenon of interest. In essence, performing spectrum analysis on a time series is like putting the series through a prism in order to identify the wave lengths and importance of underlying cyclical components. As a result of a successful analysis one might uncover just a few recurring cycles of different lengths in the time series of interest, which at first looked more or less like random noise.
|
| Наиболее известный пример применения спектрального анализа - циклическая природа солнечных пятен (например, см. Блумфилд, 1976 или Шамвэй, 1988). Оказывается, что активность солнечных пятен имеет 11-ти летний цикл. Другие примеры небесных явлений, изменения погоды, колебания в товарных ценах, экономическая активность и т. д. также часто используются в литературе для демонстрации этого метода. В отличие от АРПСС или метода экспоненциального сглаживания (см. разделы АРПСС и Экспоненциальное сглаживание), цель спектрального анализа - распознать сезонные колебания различной длины, в то время как в предшествующих типах анализа, длина сезонных компонент обычно известна (или предполагается) заранее и затем включается в некоторые теоретические модели скользящего среднего или автокорреляции.
| A much cited example for spectrum analysis is the cyclical nature of sun spot activity (e. g., see Bloomfield, 1976, or Shumway, 1988). It turns out that sun spot activity varies over 11 year cycles. Other examples of celestial phenomena, weather patterns, fluctuations in commodity prices, economic activity, etc. are also often used in the literature to demonstrate this technique. To contrast this technique with ARIMA or Exponential Smoothing, the purpose of spectrum analysis is to identify the seasonal fluctuations of different lengths, while in the former types of analysis, the length of the seasonal component is usually known (or guessed) a priori and then included in some theoretical model of moving averages or autocorrelations.
|
| Классический текст по спектральному анализу - Bloomfield (1976); однако другие подробные обсуждения могут быть найдены в Jenkins and Watts (1968), Brillinger (1975), Brigham (1974), Elliott and Rao (1982), Priestley (1981), Shumway (1988) или Wei (1989).
| The classic text on spectrum analysis is Bloomfield (1976); however, other detailed discussions can be found in Jenkins and Watts (1968), Brillinger (1975), Brigham (1974), Elliott and Rao (1982), Priestley (1981), Shumway (1988), or Wei (1989).
|
| За дальнейшей информацией обратитесь к Анализу временных рядов и следующим разделам:
| For more information, see Time Series Analysis - Index and the following topics:
|
| • Основные понятия и принципы
| Basic Notations and Principles
|
| • Быстрое преобразование Фурье
| Fast Fourier Transformations
|
| • Идентификация модели временных рядов
| Identifying Patterns in Time Series Data
|
| • АРПСС (Бокс и Дженкинс) и автокорреляции Вводный обзор АРПСС
| - ARIMA (Box & Jenkins) and Autocorrelations ARIMA Introductory Overview
|
| • Прерванные временные ряды
| |
| • Анализ распределенных лагов
| - Distributed Lags Analysis
|
| • Сезонная декомпозиция (метод Census I)
| - Seasonal Decomposition (Census I)
|
| • Экспоненциальное сглаживание
| |
| • Кросс-спектральный анализ
| |
| Кросс-спектральный анализ
| |
| • Общее введение
| |
| • Основные понятия и принципы
| |
| • Результаты для каждой переменной
| Basic Notation and Principles
|
| • Кросс-периодограмма, кросс-плотность, квадратурная плотность и кросс-амплитуда
| Results for Each Variable
|
| • Квадрат когерентности, усиление и фазовый сдвиг
| - The Cross-periodogram, Cross-density, Quadrature-density, and Cross-amplitude
|
| • Как создавались данные для примера
| - Squared Coherency, Gain, and Phase Shift
|
| За дальнейшей информацией обратитесь к Анализу временных рядов и следующим разделам:
| - How the Example Data were Created
|
| • Идентификация модели временных рядов
| - For more information, see Time Series Analysis - Index and the following topics:
|
| • АРПСС (Бокс и Дженкинс) и автокорреляции Вводный обзор АРПСС
| - Identifying Patterns in Time Series Data
|
| • Прерванные временные ряды
| - ARIMA (Box & Jenkins) and Autocorrelations ARIMA Introductory Overview
|
| • Экспоненциальное сглаживание
| Interrupted Time Series
|
| • Сезонная декомпозиция (метод Census I)
| - Exponential Smoothing Seasonal Decomposition (Census I)
|
| • Сезонная корректировка X-11 (метод Census II)
| - X-11 Census method II seasonal adjustment
|
| • Таблицы результатов корректировки X-11
| - X-11 Census method II result tables
|
| • Анализ распределенных лагов
| - Distributed Lags analysis
|
| • Одномерный анализ Фурье
| - Single Spectrum (Fourier) Analysis
|
| • Основные понятия и принципы
| - Basic Notations and Principles
|
| • Быстрое преобразование Фурье
| - Fast Fourier Transformations
|
|
|
|
| Общее введение
| General Introduction
|
| Кросс-спектральный анализ развивает Одномерный анализ Фурье и позволяет анализировать одновременно два ряда. Мы предполагаем, что вы уже прочитали введение к разделу одномерного спектрального анализа. Подробное обсуждение кросс-спектрального анализа можно найти в книгах Bloomfield (1976), Jenkins and Watts (1968), Brillinger (1975), Brigham (1974), Elliott and Rao (1982), Priestley (1981), Shumway (1988), or Wei (1989).
| Cross-spectrum analysis is an extension of Single Spectrum (Fourier) Analysis to the simultaneous analysis of two series. In the following paragraphs, we will assume that you have already read the introduction to single spectrum analysis. Detailed discussions of this technique can be found in Bloomfield (1976), Jenkins and Watts (1968), Brillinger (1975), Brigham (1974), Elliott and Rao (1982), Priestley (1981), Shumway (1988), or Wei (1989).
|
| Периодичность ряда на определенных частотах. Наиболее известный пример применения спектрального анализа - циклическая природа солнечных пятен (например, см. Блумфилд, 1976 или Шамвэй, 1988). Оказывается, что активность солнечных пятен имеет 11-ти летний цикл. Другие примеры небесных явлений, изменения погоды, колебания в товарных ценах, экономическая активность и т. д. также часто используются в литературе для демонстрации этого метода.
| Strong periodicity in the series at the respective frequency. A much cited example for spectrum analysis is the cyclical nature of sun spot activity (e. g., see Bloomfield, 1976, or Shumway, 1988). It turns out that sun spot activity varies over 11 year cycles. Other examples of celestial phenomena, weather patterns, fluctuations in commodity prices, economic activity, etc. are also often used in the literature to demonstrate this technique.
|
|
|
|
| Основные понятия и принципы
| Basic Notation and Principles
|
| Простой пример. Рассмотрим следующие два ряда с 16 наблюдениями:
| A simple example Consider the following two series with 16 cases:
|
| | ПЕРЕМ1
| ПЕРЕМ2
| | 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
| 1. 000 1. 637 1. 148 -. 058 -. 713 -. 383. 006 -. 483 -1. 441 -1. 637 -. 707. 331. 441 -. 058 -. 006. 924
| -. 058 -. 713 -. 383. 006 -. 483 -1. 441 -1. 637 -. 707. 331. 441 -. 058 -. 006. 924 1. 713 1. 365. 266
|
| | | VAR1
| VAR2
| | 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
| 1. 000 1. 637 1. 148 -. 058 -. 713 -. 383. 006 -. 483 -1. 441 -1. 637 -. 707. 331. 441 -. 058 -. 006. 924
| -. 058 -. 713 -. 383. 006 -. 483 -1. 441 -1. 637 -. 707. 331. 441 -. 058 -. 006. 924 1. 713 1. 365. 266
|
|
| С первого взгляда нелегко рассмотреть взаимосвязь между двумя рядами. Тем не менее, как показано ниже, ряды создавались так, что содержат две сильно коррелируемые периодичности. Далее показаны части таблицы результатов из кросс-спектрального анализа (спектральные оценки были сглажены окном Парзена ширины 3).
| At first sight it is not easy to see the relationship between the two series. However, as shown below the series were created so that they would contain two strong correlated periodicities. Shown below are parts of the summary from the cross-spectrum analysis (the spectral estimates were smoothed with a Parzen window of width 3).
|
| Незавмсимая (X): ПЕРЕМ1 Зависимая (Y): ПЕРЕМ2
| | Частота
| Период
| X плотность
| Y плотность
| Кросс плотность
| Кросс квадр.
| Кросс амплит.
| | 0. 000000. 062500. 125000. 187500. 250000. 312500. 375000. 437500. 500000
| 16. 00000 8. 00000 5. 33333 4. 00000 3. 20000 2. 66667 2. 28571 2. 00000
| . 000000 8. 094709. 058771 3. 617294. 333005. 091897. 052575. 040248. 037115
| . 024292 7. 798284. 100936 3. 845154. 278685. 067630. 036056. 026633 0. 000000
| -. 00000 2. 35583 -. 04755 -2. 92645 -. 26941 -. 07435 -. 04253 -. 03256 0. 00000
| 0. 00000 -7. 58781. 06059 2. 31191. 14221. 02622. 00930. 00342 0. 00000
| . 000000 7. 945114. 077020 3. 729484. 304637. 078835. 043539. 032740 0. 000000
|
| | Indep. (X): VAR1 Dep. (Y): VAR2
| | Frequncy
| Period
| X Density
| Y Density
| Cross Density
| Cross Quad
| Cross Amplit.
| | 0. 00000. 062500. 125000. 187500. 250000. 312500. 375000. 437500. 500000
| 16. 0000 8. 00000 5. 33333 4. 00000 3. 20000 2. 66667 2. 28571 2. 00000
| . 000000 8. 094709. 058771 3. 617294. 333005. 091897. 052575. 040248. 037115
| . 024292 7. 798284. 100936 3. 845154. 278685. 067630. 036056. 026633 0. 000000
| -. 00000 2. 35583 -. 04755 -2. 92645 -. 26941 -. 07435 -. 04253 -. 03256 0. 00000
| 0. 00000 -7. 58781. 06059 2. 31191. 14221. 02622. 00930. 00342 0. 00000
| . 000000 7. 945114. 077020 3. 729484. 304637. 078835. 043539. 032740 0. 000000
|
|
| Результаты для каждой переменной
| Results for Each Variable
|
| Полная таблица результатов содержит все спектральные статистики, вычисленные для каждого ряда, как описано в разделе Одномерный анализ Фурье. Взглянув на приведенные выше результаты, очевидно, что оба ряда имеют основные периодичности на частотах. 0625 и. 1875.
| The complete summary contains all spectrum statistics computed for each variable, as described in the Single Spectrum (Fourier) Analysis overview section. Looking at the results shown above, it is clear that both variables show strong periodicities at the frequencies. 0625 and. 1875.
|
|
|
|
| Кросс-периодограмма, кросс-плотность, квадратурная плотность и кросс-амплитуда
| Cross-periodogram, Cross-Density, Quadrature-density, Cross-amplitude
|
| Аналогично результатам для одной переменной, полная итоговая таблица результатов также покажет значения периодограммы для кросс-периодограммы. Однако кросс-спектр состоит из комплексных чисел, которые могут быть разделены на действительную и мнимую части. Они могут быть сглажены для вычисления оценок кросс-плотности и квадратурной плотности (квадр-плотность для краткости), соответственно. (Причины сглаживания и различные функции весов для сглаживания обсуждаются в разделе Одномерный анализ Фурье. ) Квадратный корень из суммы квадратов значений кросс-плотности и квадр-плотности называется кросс-амплитудой. Кросс-амплитуда может интерпретироваться как мера ковариации между соответствующими частотными компонентами двух рядов. Таким образом из результатов, показанных в таблице результатов выше, можно заключить, что частотные компоненты. 0625 и. 1875 двух рядов взаимосвязаны.
| Analogous to the results for the single variables, the complete summary will also display periodogram values for the cross periodogram. However, the cross-spectrum consists of complex numbers that can be divided into a real and an imaginary part. These can be smoothed to obtain the cross-density and quadrature density (quad density for short) estimates, respectively. (The reasons for smoothing, and the different common weight functions for smoothing are discussed in the Single Spectrum (Fourier) Analysis. ) The square root of the sum of the squared cross-density and quad-density values is called the cross- amplitude. The cross-amplitude can be interpreted as a measure of covariance between the respective frequency components in the two series. Thus we can conclude from the results shown in the table above that the. 0625 and. 1875 frequency components in the two series covary.
|
|
|
|
| Квадрат когерентности, усиление и фазовый сдвиг
| Squared Coherency, Gain, and Phase Shift
|
| Существуют дополнительные статистики, которые будут показаны в полной итоговой таблице результатов.
| There are additional statistics that can be displayed in the complete summary.
|
| Квадрат когерентности. Можно нормировать значения кросс-амплитуды, возведя их в квадрат и разделив на произведение оценок спектральной плотности каждого ряда. Результат называется квадратом когерентности, который может быть проинтерпретирован как квадрат коэффициента корреляции (см. раздел Корреляции); т. е. значение когерентности - это квадрат корреляции между циклическими компонентами двух рядов соответствующей частоты. Однако значения когерентности не следует объяснять таким образом; например, когда оценки спектральной плотности обоих рядов очень малы, могут получиться большие значения когерентности (делитель в выражении когерентности может быть очень маленьким), даже если нет существенных циклических компонент в каждом ряду соответствующей частоты.
| Squared coherency. One can standardize the cross-amplitude values by squaring them and dividing by the product of the spectrum density estimates for each series. The result is called the squared coherency, which can be interpreted similar to the squared correlation coefficient (see Correlations - Overview), that is, the coherency value is the squared correlation between the cyclical components in the two series at the respective frequency. However, the coherency values should not be interpreted by themselves; for example, when the spectral density estimates in both series are very small, large coherency values may result (the divisor in the computation of the coherency values will be very small), even though there are no strong cyclical components in either series at the respective frequencies.
|
| Усиление. Значение усиления в анализе вычисляется делением значения кросс-амплитуды на оценки спектральной плотности одного или двух рядов. Следовательно, может быть вычислено два значения усиления, которые могут интерпретироваться как стандартные коэффициенты регрессии, соответствующей частоты, полученные методом наименьших квадратов.
| Gain. The gain value is computed by dividing the cross-amplitude value by the spectrum density estimates for one of the two series in the analysis. Consequently, two gain values are computed, which can be interpreted as the standard least squares regression coefficients for the respective frequencies.
|
| Фазовый сдвиг. В заключение, оценки фазового сдвига вычисляются как арктангенс (tan**-1) коэффициента пропорциональности оценки квадр-плотности и оценки кросс-плотности. Оценки фазового сдвига (обычно обозначаемые греческой буквой y) измеряют, насколько каждая частотная компонента одного ряда опережает частотные компоненты другого.
| Phase shift. Finally, the phase shift estimates are computed as tan**-1 of the ratio of the quad density estimates over the cross-density estimate. The phase shift estimates (usually denoted by the Greek letter ) are measures of the extent to which each frequency component of one series leads the other.
|
|
|
|
| Как создавались данные для примера
| How the Example Data were Created
|
| Теперь вернемся к примеру данных, приведенному выше. Большие оценки спектральной плотности для обоих рядов и значения кросс-амплитуды для частот = 0. 0625 и =. 1875 предполагают две существенных синхронных периодичности с этими частотами в обоих рядах. Фактически, два ряда создавались как:
| Now, let us return to the example data set presented above. The large spectral density estimates for both series, and the cross-amplitude values at frequencies  = 0. 0625 and = 0. 0625 and  =. 1875 suggest two strong synchronized periodicities in both series at those frequencies. In fact, the two series were created as: =. 1875 suggest two strong synchronized periodicities in both series at those frequencies. In fact, the two series were created as:
|
| v1 = cos(2*π *. 0625*(v0-1)) +. 75*sin(2*π *. 2*(v0-1))
| v1 = cos(2*π *. 0625*(v0-1)) +. 75*sin(2*π *. 2*(v0-1))
|
| v2 = cos(2*π *. 0625*(v0+2)) +. 75*sin(2*π *. 2*(v0+2))
| v2 = cos(2*π *. 0625*(v0+2)) +. 75*sin(2*π *. 2*(v0+2))
|
| (где v0 - номер наблюдения). Действительно, анализ, представленный в этом обзоре, очень хорошо воспроизводит периодичность, заложенную в данные.
| (where v0 is the case number). Indeed, the analysis presented in this overview reproduced the periodicity " inserted" into the data very well.
|
| Спектральный анализ - Основные понятия и принципы
| Spectrum Analysis - Basic Notation and Principles
|
| • Частота и период
| Frequency and Period
|
| • Общая структура модели
| - The General Structural Model
|
| • Простой пример
| |
| • Периодограмма
| |
| • Проблема рассеяния
| |
| • Добавление констант во временной ряд (пэддинг)
| |
| • Косинус-сглаживание
| |
| • Окна данных и оценки спектральной плотности
| - Data Windows and Spectral Density Estimates
|
| • Подготовка данных к анализу
| - Preparing the Data for Analysis
|
| • Результаты для случая, когда в ряде отсутствует периодичность
| - Results when no Periodicity in the Series Exists
|
| За дальнейшей информацией обратитесь к Анализу временных рядов и следующим разделам:
| - For more information, see Time Series Analysis - Index and the following topics:
|
| • Идентификация модели временных рядов
| Identifying Patterns in Time Series Data
|
| • АРПСС (Бокс и Дженкинс) и автокорреляции Вводный обзор АРПСС
| - ARIMA (Box & Jenkins) and Autocorrelations ARIMA Introductory Overview
|
| • Прерванные временные ряды
| |
| • Экспоненциальное сглаживание
| |
| • Сезонная декомпозиция (метод Census I)
| - Seasonal Decomposition (Census I)
|
| • Сезонная корректировка X-11 (метод Census II)
| - X-11 Census method II seasonal adjustment
|
| • Таблицы результатов корректировки X-11
| - X-11 Census method II result tables
|
| • Анализ распределенных лагов
| - Distributed Lags Analysis
|
| • Одномерный анализ Фурье
| - Single Spectrum (Fourier) Analysis
|
| • Кросс-спектральный анализ
| |
| • Быстрое преобразование Фурье
| - Fast Fourier Transformations
|
| Частота и период
| |
| Длина волны функций синуса или косинуса, как правило, выражается числом циклов (периодов) в единицу времени (Частота), часто обозначается греческой буквой ню (ν; в некоторых учебниках также используют f). Например, временной ряд, состоящий из количества писем, обрабатываемых почтой, может иметь 12 циклов в году. Первого числа каждого месяца отправляется большое количество корреспонденции (много счетов приходит именно первого числа каждого месяца); затем, к середине месяца, количество корреспонденции уменьшается; и затем вновь возрастает к концу месяца. Поэтому каждый месяц колебания в количестве корреспонденции, обрабатываемой почтовым отделением, будут проходить полный цикл. Таким образом, если единица анализа - один год, то ν будет равно 12 (поскольку имеется 12 циклов в году). Конечно, могут быть и другие циклы с различными частотами. Например, годичные циклы (ν =1) и, возможно, недельные циклы (ν =52 недели в год).
| The " wave length" of a sine or cosine function is typically expressed in terms of the number of cycles per unit time (Frequency), often denoted by the Greek letter nu (ν; some text books also use f). For example, the number of letters handled in a post office may show 12 cycles per year: On the first of every month a large amount of mail is sent (many bills come due on the first of the month), then the amount of mail decreases in the middle of the month, then it increases again towards the end of the month. Therefore, every month the fluctuation in the amount of mail handled by the post office will go through a full cycle. Thus, if the unit of analysis is one year, then n would be equal to 12, as there would be 12 cycles per year. Of course, there will likely be other cycles with different frequencies. For example, there might be annual cycles (ν =1), and perhaps weekly cycles < (ν =52 weeks per year).
|
| Период Т функций синуса или косинуса определяется как продолжительность по времени полного цикла. Таким образом, это обратная величина к частоте: T = 1/ν. Возвратимся к примеру с почтой из предыдущего абзаца, здесь месячный цикл будет равен 1/12 = 0. 0833 года. Другими словами, это период составляет 0. 0833 года.
| The period T of a sine or cosine function is defined as the length of time required for one full cycle. Thus, it is the reciprocal of the frequency, or: T = 1/ν. To return to the mail example in the previous paragraph, the monthly cycle, expressed in yearly terms, would be equal to 1/12 = 0. 0833. Put into words, there is a period in the series of length 0. 0833 years.
|
|
|
|
| Общая структура модели
| The General Structural Model
|
| Как было отмечено ранее, цель спектрального анализа - разложить ряд на функции синусов и косинусов различных частот, для определения тех, появление которых особенно существенно и значимо. Один из возможных способов сделать это - решить задачу линейной множественной регрессии (см. раздел Множественная регрессия), где зависимая переменная -наблюдаемый временной ряд, а независимые переменные или регрессоры: функции синусов всех возможных (дискретных) частот. Такая модель линейной множественной регрессии может быть записана как:
| As mentioned before, the purpose of spectrum analysis is to decompose the original series into underlying sine and cosine functions of different frequencies, in order to determine those that appear particularly strong or important. One way to do so would be to cast the issue as a linear Multiple Regression problem, where the dependent variable is the observed time series, and the independent variables are the sine functions of all possible (discrete) frequencies. Such a linear multiple regression model may be written as:
|
| xt = a0 + Σ [ak*cos(λ k*t) + bk*sin(λ k*t)] (для k = 1 до q)
| xt = a0 + Σ [ak*cos(λ k*t) + bk*sin(λ k*t)] (для k = 1 до q)
|
| Следующее общее понятие классического гармонического анализа в этом уравнении - λ (лямбда) -это круговая частота, выраженная в радианах в единицу времени, т. е. λ = 2*π *ν k, где π - константа пи = 3. 1416 и ν k = k/q. Здесь важно осознать, что вычислительная задача подгонки функций синусов и косинусов разных длин к данным может быть решена с помощью множественной линейной регрессии. Заметим, что коэффициенты ak при косинусах и коэффициенты bk при синусах - это коэффициенты регрессии, показывающие степень, с которой соответствующие функции коррелируют с данными [заметим, что сами синусы и косинусы на различных частотах не коррелированы или, другим языком, ортогональны. Таким образом, мы имеем дело с частным случаем разложения по ортогональным полиномам. ] Всего существует q различных синусов и косинусов (см. также Множественная регрессия); интуитивно ясно, что число функций синусов и косинусов не может быть больше числа данных в ряде. Не вдаваясь в подробности, отметим, если n - количество данных, то будет n/2+1 функций косинусов и n/2-1 функций синусов. Другими словами, различных синусоидальных волн будет столько же, сколько данных, и вы сможете полностью воспроизвести ряд по основным функциям. (Заметим, если количество данных в ряде нечетно, то последнее наблюдение обычно опускается. Для определения синусоидальной функции нужно иметь, по крайней мере, две точки: высокого и низкого пика. )
| Following the common notation from classical harmonic analysis, in this equation λ (lambda) is the frequency expressed in terms of radians per unit time, that is: λ = 2*π *ν k, where π is the constant pi=3. 14... and ν k = k/q. What is important here is to recognize that the computational problem of fitting sine and cosine functions of different lengths to the data can be considered in terms of multiple linear regression. Note that the cosine parameters ak and sine parameters bk are regression coefficients that tell us the degree to which the respective functions are correlated with the data. Overall there are q different sine and cosine functions; intuitively (as also discussed in Multiple Regression), it should be clear that we cannot have more sine and cosine functions than there are data points in the series. Without going into detail, if there are N data points in the series, then there will be N/2+1 cosine functions and N/2-1 sine functions. In other words, there will be as many different sinusoidal waves as there are data points, and we will be able to completely reproduce the series from the underlying functions. (Note that if the number of cases in the series is odd, then the last data point will usually be ignored; in order for a sinusoidal function to be identified, you need at least two points: the high peak and the low peak. )
|
| В итоге, спектральный анализ определяет корреляцию функций синусов и косинусов различной частоты с наблюдаемыми данными. Если найденная корреляция (коэффициент при определенном синусе или косинусе) велика, то можно заключить, что существует строгая периодичность на соответствующей частоте в данных.
| To summarize, spectrum analysis will identify the correlation of sine and cosine functions of different frequency with the observed data. If a large correlation (sine or cosine coefficient) is identified, one can conclude that there is a strong periodicity of the respective frequency (or period) in the data.
|
| Комплексные числа (действительные и мнимые числа). Во многих учебниках по спектральному анализу структурная модель, показанная выше, представлена в комплексных числах; т. е. параметры оцениваемого процесса описаны с помощью действительной и мнимой части преобразования Фурье. Комплексное число состоит из действительного и мнимого числа. Мнимые числа, по определению, - это числа, умноженные на константу i, где i определяется как квадратный корень из -1. Очевидно, корень квадратный из -1 не существует в обычном сознании (отсюда термин мнимое число); однако арифметические операции над мнимыми числами могут производиться естественным образом [например, (i*2)**2= -4]. Полезно представление действительных и мнимых чисел, образующих двумерную координатную плоскость, где горизонтальная или X-ось представляет все действительные числа, а вертикальная или Y-ось представляет все мнимые числа. Комплексные числа могут быть представлены точками на двумерной плоскости. Например, комплексное число 3+i*2 может быть представлено точкой с координатами {3, 2} на этой плоскости. Можно также представить комплексные числа как углы; например, можно соединить точку, соответствующую комплексному числу на плоскости с началом координат (комплексное число 0+i*0), и измерить угол наклона этого вектора к горизонтальной оси. Таким образом интуитивно ясно, каким образом формула спектрального разложения, показанная выше, может быть переписана в комплексной области. В таком виде математические вычисления часто более изящны и проще в выполнении, поэтому многие учебники предпочитают представление спектрального анализа в комплексных числах.
| Complex numbers (real and imaginary numbers). In many text books on spectrum analysis, the structural model shown above is presented in terms of complex numbers, that is, the parameter estimation process is described in terms of the Fourier transform of a series into real and imaginary parts. Complex numbers are the superset that includes all real and imaginary numbers. Imaginary numbers, by definition, are numbers that are multiplied by the constant i, where i is defined as the square root of -1. Obviously, the square root of -1 does not exist, hence the term imaginary number; however, meaningful arithmetic operations on imaginary numbers can still be performed (e. g., [i*2]**2= -4). It is useful to think of real and imaginary numbers as forming a two dimensional plane, where the horizontal or X-axis represents all real numbers, and the vertical or Y-axis represents all imaginary numbers. Complex numbers can then be represented as points in the two- dimensional plane. For example, the complex number 3+i*2 can be represented by a point with coordinates {3, 2} in this plane. One can also think of complex numbers as angles, for example, one can connect the point representing a complex number in the plane with the origin (complex number 0+i*0), and measure the angle of that vector to the horizontal line. Thus, intuitively one can see how the spectrum decomposition formula shown above, consisting of sine and cosine functions, can be rewritten in terms of operations on complex numbers. In fact, in this manner the mathematical discussion and required computations are often more elegant and easier to perform; which is why many text books prefer the presentation of spectrum analysis in terms of complex numbers.
|
|
|
|
| Простой пример
| A Simple Example
|
| Шамвэй (1988) предлагает следующий простой пример для объяснения спектрального анализа. Создадим ряд из 16 наблюдений, полученных из уравнения, показанного ниже, а затем посмотрим, каким образом можно извлечь из него информацию. Сначала создадим переменную и определим ее как:
| Shumway (1988) presents a simple example to clarify the underlying " mechanics" of spectrum analysis. Let us create a series with 16 cases following the equation shown above, and then see how we may " extract" the information that was put in it. First, create a variable and define it as:
|
| x = 1*cos(2*π *. 0625*(v0-1)) +. 75*sin(2*π *. 2*(v0-1))
| x = 1*cos(2*π *. 0625*(v0-1)) +. 75*sin(2*π *. 2*(v0-1))
|
| Эта переменная состоит из двух основных периодичностей - первая с частотой ν =. 0625 (или периодом 1/ν =16; одно наблюдение составляет 1/16-ю длины полного цикла, или весь цикл содержит каждые 16 наблюдений) и вторая с частотой ν =. 2 (или периодом 5). Коэффициент при косинусе (1. 0) больше чем коэффициент при синусе (. 75). Итоговая таблица результатов спектрального анализа показана ниже.
| This variable is made up of two underlying periodicities: The first at the frequency of ν =. 0625 (or period 1/ν =16; one observation completes 1/16'th of a full cycle, and a full cycle is completed every 16 observations) and the second at the frequency of ν =. 2 (or period of 5). The cosine coefficient (1. 0) is larger than the sine coefficient (. 75). The spectrum analysis summary are shown below.
|
| |
Спектральный анализ: ПЕРЕМ1 (shumex. sta) Число наблюдений: 16
| | t
| Час- тота
| Период
| Косинус корэфф.
| Синус корэфф.
| Периодо- грамма
| | 0 1 2 3 4 5 6 7 8
| . 0000. 0625. 1250. 1875. 2500. 3125. 3750. 4375. 5000
| 16. 00 8. 00 5. 33 4. 00 3. 20 2. 67 2. 29 2. 00
| . 000 1. 006. 033. 374 -. 144 -. 089 -. 075 -. 070 -. 068
| 0. 000. 028. 079. 559 -. 144 -. 060 -. 031 -. 014 0. 000
| . 000 8. 095. 059 3. 617. 333. 092. 053. 040. 037
|
| | |
Spectral analysis: VAR1 (shumex. sta) No. of cases: 16
| | t
| Freq- uency
| Period
| Cosine Coeffs
| Sine Coeffs
| Period- ogram
| | 0 1 2 3 4 5 6 7 8
| . 0000. 0625. 1250. 1875. 2500. 3125. 3750. 4375. 5000
| 16. 00 8. 00 5. 33 4. 00 3. 20 2. 67 2. 29 2. 00
| . 000 1. 006. 033. 374 -. 144 -. 089 -. 075 -. 070 -. 068
| 0. 000. 028. 079. 559 -. 144 -. 060 -. 031 -. 014 0. 000
| . 000 8. 095. 059 3. 617. 333. 092. 053. 040. 037
| .
|
| Теперь рассмотрим столбцы таблицы результатов. Ясно, что наибольший коэффициент при косинусах расположен напротив частоты. 0625. Наибольший коэффициент при синусах соответствует частоте. 1875. Таким образом, эти две частоты, которые были " внесены" в данные, отчетливо проявились.
| Let us now review the columns. Clearly, the largest cosine coefficient can be found for the. 0625 frequency. A smaller sine coefficient can be found at frequency =. 1875. Thus, clearly the two sine/cosine frequencies which were " inserted" into the example data file are reflected in the above table
|
|
|
|
| Периодограмма
| Periodogram
|
| Функции синусов и косинусов независимы (или ортогональны); поэтому можно просуммировать квадраты коэффициентов для каждой частоты, чтобы вычислить периодограмму. Более часто, значения периодограммы вычисляются как:
| The sine and cosine functions are mutually independent (or orthogonal); thus we may sum the squared coefficients for each frequency to obtain the periodogram. Specifically, the periodogram values above are computed as:
|
| Pk = синус-коэффициентk2 + косинус-коэффициентk2 * N/2
| Pk = sine coefficientk2 + cosine coefficientk2 * N/2
|
| где Pk - значения периодограммы на частоте ν k, и N - общая длина ряда. Значения периодограммы можно интерпретировать как дисперсию (вариацию) данных на соответствующей частоте. Обычно значения периодограммы изображаются в зависимости от частот или периодов.
| where Pk is the periodogram value at frequency ν k and N is the overall length of the series. The periodogram values can be interpreted in terms of variance (sums of squares) of the data at the respective frequency or period. Customarily, the periodogram values are plotted against the frequencies or periods.
|
| 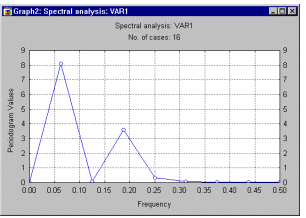
|
|
|
|
| Проблема рассеяния
| The Problem of Leakage
|
| В примере, приведенном выше, функция синуса с частотой 0. 2 была " вставлена" в ряд. Однако из-за того, что длина ряда равна 16, ни одна из частот, полученных в таблице результатов, не совпадает в точности с этой частотой. На практике в этих случаях часто оказывается, что соответствующая частота " рассеивается" на близкие частоты. Например, могут быть найдены большие значения периодограммы для двух близких частот, когда в действительности существует только одна основная функция синуса или косинуса с частотой, которая попадает на одну из этих частот или лежит между найденными частотами. Существует три подхода к решению проблемы рассеяния:
| In the example above, a sine function with a frequency of 0. 2 was " inserted" into the series. However, because of the length of the series (16), none of the frequencies reported exactly " hits" on that frequency. In practice, what often happens in those cases is that the respective frequency will " leak" into adjacent frequencies. For example, one may find large periodogram values for two adjacent frequencies, when, in fact, there is only one strong underlying sine or cosine function at a frequency that falls in-between those implied by the length of the series. There are three ways in which one can approach the problem of leakage:
|
| При помощи добавление констант во временной ряда ряда можно увеличить частоты,
| By padding the series one may apply a finer frequency " roster" to the data,
|
| Применяя сглаживание ряда перед анализом, можно уменьшить рассеяние или
| By tapering the series prior to the analysis one may reduce leakage, or
|
| Применяя сглаживание периодограммы, можно идентифицировать основные частотные области или (спектральные плотности), которые существенно влияют на циклическое поведение ряда.
| By smoothing the periodogram one may identify the general frequency " regions" or (spectral densities) that significantly contribute to the cyclical behavior of the series.
|
| Ниже смотрите описание каждого из этих подходов.
| See below for descriptions of each of these approaches.
|
|
|
|
| Добавление констант во временной ряд (пэддинг)
| Padding the Time Series
|
| Так как частотные величины вычисляются как N/t, можно просто добавить в ряд константы (например, нули), и таким образом получить увеличение частот. Фактически, если вы добавите в файл данных, описанный в примере выше, десять нулей, результаты не изменятся; т. е. наибольшие пики периодограммы будут находиться по-прежнему на частотах близких к. 0625 и. 2. (Добавление констант во временной ряд также часто желательно для увеличения вычислительной эффективности; см. ниже. )
| Because the frequency values are computed as N/t (the number of units of times) one may simply pad the series with a constant (e. g., zeros) and thereby introduce smaller increments in the frequency values. In a sense, padding allows one to apply a finer roster to the data. In fact, if we padded the example data file described in the example above with ten zeros, the results would not change, that is, the largest periodogram peaks would still occur at the frequency values closest to. 0625 and. 2. (Padding is also often desirable for computational efficiency reasons; see below. )
|
|
|
|
| Косинус-сглаживание
| Tapering
|
| Так называемый процесс косинус-сглаживания - рекомендуемое преобразование ряда, предшествующее спектральному анализу. Оно обычно приводит к уменьшению рассеяния в периодограмме. Логическое обоснование этого преобразования подробно объясняется в книге Bloomfield (1976, стр. 80-94). По существу, количественное отношение (p) данных в начале и в конце ряда преобразуется при помощи умножения на веса:
| The so-called process of split-cosine-bell tapering is a recommended transformation of the series prior to the spectrum analysis. It usually leads to a reduction of leakage in the periodogram. The rationale for this transformation is explained in detail in Bloomfield (1976, p. 80-94). In essence, a proportion (p) of the data at the beginning and at the end of the series is transformed via multiplication by the weights:
|
| wt = 0. 5*{1-cos[π *(t - 0. 5)/m]} (для t=0 до m-1) wt = 0. 5*{1-cos[π *(N - t + 0. 5)/m]} (для t=N-m до N-1)
| wt = 0. 5*{1-cos[π *(t - 0. 5)/m]} (для t=0 до m-1) wt = 0. 5*{1-cos[π *(N - t + 0. 5)/m]} (для t=N-m до N-1)
|
| где m выбирается так, чтобы 2*m/N было равно коэффициенту пропорциональности сглаживаемых данных (p).
| where m is chosen so that 2*m/N is equal to the proportion of data to be tapered (p).
|
|
|
|
| Окна данных и оценки спектральной плотности
| Data Windows and Spectral Density Estimates
|
| На практике, при анализе данных обычно не очень важно точно определить частоты основных функций синусов или косинусов. Скорее, т. к. значения периодограммы - объект существенного случайного колебания, можно столкнуться с проблемой многих хаотических пиков периодограммы. В этом случае хотелось бы найти частоты с большими спектральными плотностями, т. е. частотные области, состоящие из многих близких частот, которые вносят наибольший вклад в периодическое поведение всего ряда. Это может быть достигнуто путем сглаживания значений периодограммы с помощью преобразования взвешенного скользящего среднего. Предположим, ширина окна скользящего среднего равна m (должно быть нечетным числом); следующие наиболее часто используемые преобразования (заметим: p = (m-1)/2).
| In practice, when analyzing actual data, it is usually not of crucial importance to identify exactly the frequencies for particular underlying sine or cosine functions. Rather, because the periodogram values are subject to substantial random fluctuation, one is faced with the problem of very many " chaotic" periodogram spikes. In that case, one would like to find the frequencies with the greatest spectral densities, that is, the frequency regions, consisting of many adjacent frequencies, that contribute most to the overall periodic behavior of the series. This can be accomplished by smoothing the periodogram values via a weighted moving average transformation. Suppose the moving average window is of width m (which must be an odd number); the following are the most commonly used smoothers (note: p = (m-1)/2).
|
- Окно Даниэля (равные веса). Окно Даниэля (Daniell, 1946) означает простое (с равными весами) сглаживание скользящим средним значений периодограммы; т. е. каждая оценка спектральной плотности вычисляется как среднее m/2 предыдущих и последующих значений периодограммы.
| Daniell (or equal weight) window. The Daniell window (Daniell 1946) amounts to a simple (equal weight) moving average transformation of the periodogram values, that is, each spectral density estimate is computed as the mean of the m/2 preceding and subsequent periodogram values.
|
- Окно Тьюки. В окне Тьюки (Blackman and Tukey, 1958) или Тьюки-Ханна (Hanning) (названное в честь Julius Von Hann), для каждой частоты веса для взвешенного скользящего среднего значений периодограммы вычисляются как:
| Tukey window. In the Tukey (Blackman and Tukey, 1958) or Tukey-Hanning window (named after Julius Von Hann), for each frequency, the weights for the weighted moving average of the periodogram values are computed as:
|
- wj = 0. 5 + 0. 5*cos(π *j/p) (для j=0 до p) w-j = wj (для j
 0) 0) | - wj = 0. 5 + 0. 5*cos(π *j/p) (для j=0 до p) w-j = wj (для j
 0) 0) |
| Окно Хемминга. В окне Хемминга (названного в честь R. W. Hamming) или Тьюки-Хемминга (Blackman and Tukey, 1958), для каждой частоты, веса для взвешенного скользящего среднего значений периодограммы вычисляются как:
| Hamming window. In the Hamming (named after R. W. Hamming) window or Tukey-Hamming window (Blackman and Tukey, 1958), for each frequency, the weights for the weighted moving average of the periodogram values are computed as:
|
| wj = 0. 54 + 0. 46*cos(π *j/p) (для j=0 до p) w-j = wj (для j ≠ 0)
| wj = 0. 54 + 0. 46*cos(π *j/p) (для j=0 до p) w-j = wj (для j ≠ 0)
|
| Окно Парзена. В окне Парзена (Parzen, 1961), для каждой частоты, веса для взвешенного скользящего среднего значений периодограммы вычисляются как:
| Parzen window. In the Parzen window (Parzen, 1961), for each frequency, the weights for the weighted moving average of the periodogram values are computed as:
|
| wj = 1-6*(j/p)2 + 6*(j/p)3 (для j = 0 до p/2) wj = 2*(1-j/p)3 (для j = p/2 + 1 до p) w-j = wj (для j ≠ 0)
| wj = 1-6*(j/p)2 + 6*(j/p)3 (for j = 0 to p/2) wj = 2*(1-j/p)3 (for j = p/2 + 1 to p) w-j = wj (for j ≠ 0)
|
| Окно Бартлетта. В окне Бартлетта (Bartlett, 1950) веса вычисляются как:
| Bartlett window. In the Bartlett window (Bartlett, 1950) the weights are computed as:
|
| wj = 1-(j/p) (для j = 0 до p) w-j = wj (для j ≠ 0)
| wj = 1-(j/p) (for j = 0 to p) w-j = wj (for j ≠ 0)
|
| За исключением окна Даниэля, все весовые функции приписывают больший вес сглаживаемому наблюдению, находящемуся в центре окна и меньшие веса значениям по мере удаления от центра. Во многих случаях, все эти окна данных получают очень похожие результаты.
| With the exception of the Daniell window, all weight functions will assign the greatest weight to the observation being smoothed in the center of the window, and increasingly smaller weights to values that are further away from the center. In many cases, all of these data windows will produce very similar results
|
|
|
|
| Подготовка данных к анализу
| Preparing the Data for Analysis
|
| Теперь рассмотрим несколько других практических моментов спектрального анализа. Обычно, полезно вычесть среднее из значений ряда и удалить тренд (чтобы добиться стационарности) перед анализом. Иначе периодограмма и спектральная плотность " забьются" очень большим значением первого коэффициента при косинусе (с частотой 0. 0). По существу, среднее - это цикл частоты 0 (нуль) в единицу времени; т. е. константа. Аналогично, тренд также не представляет интереса, когда нужно выделить периодичность в ряде. Фактически оба этих эффекта могут заслонить более интересные периодичности в данных, поэтому и среднее, и (линейный) тренд следует удалить из ряда перед анализом. Иногда также полезно сгладить данные перед анализом, чтобы убрать случайный шум, который может засорять существенные периодические циклы в периодограмме.
| - Let us now consider a few other practical points in spectrum analysis. Usually, one wants to subtract the mean from the series, and detrend the series (so that it is stationary) prior to the analysis. Otherwise the periodogram and density spectrum will mostly be " overwhelmed" by a very large value for the first cosine coefficient (for frequency 0. 0). In a sense, the mean is a cycle of frequency 0 (zero) per unit time; that is, it is a constant. Similarly, a trend is also of little interest when one wants to uncover the periodicities in the series. In fact, both of those potentially strong effects may mask the more interesting periodicities in the data, and thus both the mean and the trend (linear) should be removed from the series prior to the analysis. Sometimes, it is also useful to smooth the data prior to the analysis, in order to " tame" the random noise that may obscure meaningful periodic cycles in the periodogram.
|
|
|
|
| Результаты для случая, когда в ряде отсутствует периодичность
| Results when no Periodicity in the Series Exists
|
| В заключение, зададим вопрос: что, если повторяющихся циклов в данных нет, т. е. если каждое наблюдение совершенно независимо от всех других наблюдений? Если распределение наблюдений соответствует нормальному, такой временной ряд может быть белым шумом (подобный белый шум можно услышать, настраивая радио). Если исходный ряд - белый шум, то значения периодограммы будут иметь экспоненциальное распределение. Таким образом, проверкой на экспоненциальность значений периодограммы можно узнать, отличается ли исходный ряд от белого шума. Пользователь может также построить одновыборочную статистику d статистику Колмогорова-Смирнова (cм. также раздел Непараметрическая статистика и распределения).
| Finally, what if there are no recurring cycles in the data, that is, if each observation is completely independent of all other observations? If the distribution of the observations follows the normal distribution, such a time series is also referred to as a white noise series (like the white noise one hears on the radio when tuned in-between stations). A white noise input series will result in periodogram values that follow an exponential distribution. Thus, by testing the distribution of periodogram values against the exponential distribution, one may test whether the input series is different from a white noise series. In addition, the you can also request to compute the Kolmogorov-Smirnov one-sample d statistic (see also Nonparametrics and Distributions for more details).
|
| Проверка, что шум - белый в ограниченной полосе частот. Заметим, что также можно получить значения периодограммы для ограниченной частотной области. Снова, если введенный ряд - белый шум с соответствующими частотами (т. е. если нет существенных периодических циклов этих частот), то распределение значений периодограммы должно быть снова экспоненциальным.
| Testing for white noise in certain frequency bands. Note that you can also plot the periodogram values for a particular frequency range only. Again, if the input is a white noise series with respect to those frequencies (i. e., it there are no significant periodic cycles of those frequencies), then the distribution of the periodogram values should again follow an exponential distribution.
|
| Быстрое преобразование Фурье (БПФ)
| Fast Fourier Transforms (FFT)
|
| • Общее введение
| · General Introduction
|
| • Вычисление БПФ во временных рядах
| · Computation of FFT in Time Series
|
| За дальнейшей информацией обратитесь к Анализу временных рядов и следующим разделам:
| · For more information, see Time Series Analysis - Index and the following topics:
|
| • Идентификация модели временных рядов
| - Identifying Patterns in Time Series Data
|
| • АРПСС (Бокс и Дженкинс) и автокорреляции Вводный обзор АРПСС
| - ARIMA (Box & Jenkins) and Autocorrelations ARIMA Introductory Overview
|
| • Прерванные временные ряды
| |
| • Экспоненциальное сглаживание
| |
| • Сезонная декомпозиция (метод Census I)
| - Seasonal Decomposition (Census I)
|
| • Сезонная корректировка X-11 (метод Census II)
| · X-11 Census method II seasonal adjustment
|
| • Таблицы результатов корректировки X-11
| · X-11 Census method II result tables
|
| • Анализ распределенных лагов
| · Distributed Lags Analysis
|
| • Одномерный анализ Фурье
| · Single Spectrum (Fourier) Analysis
|
| • Кросс-спектральный анализ
| · Cross-spectrum Analysis
|
| • Основные понятия и принципы
| · Basic Notations and Principles
|
|
|
|
| Общее введение
| General Introduction
|
| Интерпретация результатов спектрального анализа обсуждается в разделе Основные понятия и принципы, однако там мы не обсуждали вычислительные проблемы, которые в действительности очень важны. До середины 1960-х для представления спектрального разложения использовались точные формулы для нахождения параметров синусов и косинусов. Соответствующие вычисления требовали как минимум N**2 (комплексных) умножений. Таким образом, даже сегодня высокоскоростному компьютеру потребовалось бы очень много времени для анализа даже небольшого временного ряда (для 8, 000 наблюдений потребовалось бы по меньшей мере 64 миллиона умножений).
| The interpretation of the results of spectrum analysis is discussed in the Basic Notation and Principles topic, however, we have not described how it is done computationally. Up until the mid-1960s the standard way of performing the spectrum decomposition was to use explicit formulae to solve for the sine and cosine parameters. The computations involved required at least N**2 (complex) multiplications. Thus, even with today's high-speed computers, it would be very time consuming to analyze even small time series (e. g., 8, 000 observations would result in at least 64 million multiplications).
|
| Ситуация кардинально изменилась с открытием так называемого алгоритма быстрого преобразования Фурье, или БПФ для краткости. Достаточно сказать, что при применении алгоритма БПФ время выполнения спектрального анализа ряда длины N стало пропорционально N*log2(N) что конечно является огромным прогрессом.
| The time requirements changed drastically with the development of the so-called fast Fourier transform algorithm, or FFT for short. In the mid-1960s, J. W. Cooley and J. W. Tukey (1965) popularized this algorithm which, in retrospect, had in fact been discovered independently by various individuals. Various refinements and improvements of this algorithm can be found in Monro (1975) and Monro and Branch (1976). Readers interested in the computational details of this algorithm may refer to any of the texts cited in the overview. Suffice it to say that via the FFT algorithm, the time to perform a spectral analysis is proportional to N*log2(N) -- a huge improvement.
|
| Однако недостаток стандартного алгоритма БПФ состоит в том, что число данных ряда должно быть равным степени 2 (т. е. 16, 64, 128, 256, ... ). Обычно это приводит к необходимости добавлять нули во временной ряд, который, как описано выше, в большинстве случаев не меняет характерные пики периодограммы или оценки спектральной плотности. Тем не менее, в некоторых случаях, когда единица времени значительна, добавление констант во временной ряд может сделать результаты более громоздкими.
| However, a draw-back of the standard FFT algorithm is that the number of cases in the series must be equal to a power of 2 (i. e., 16, 64, 128, 256, ... ). Usually, this necessitated padding of the series, which, as described above, will in most cases not change the characteristic peaks of the periodogram or the spectral density estimates. In cases, however, where the time units are meaningful, such padding may make the interpretation of results more cumbersome.
|
|
|
|
| Вычисление БПФ во временных рядах
| Computation of FFT in Time Series
|
| Выполнение быстрого преобразования Фурье чрезвычайно эффективно. На большинстве стандартных компьютеров, ряд с более чем 100, 000 наблюдений легко анализируется. Однако существует несколько моментов, которые надо помнить при анализе рядов большого размера.
| The implementation of the FFT algorithm allows you to take full advantage of the savings afforded by this algorithm. On most standard computers, series with over 100, 000 cases can easily be analyzed. However, there are a few things to remember when analyzing series of that size.
|
| Как упоминалось ранее, для применения стандартного (и наиболее эффективного) алгоритма БПФ требуется, чтобы длина исходного ряда была равна степени 2. Если это не так, должны быть проведены дополнительные вычисления. Будут использоваться простые точные вычислительные формулы, пока исходный ряд относительно мал, и вычисления можно выполнить за относительно короткое время. Для длинных временных рядов, чтобы применить алгоритм БПФ, используется основной подход, описанный Monro и Branch (1976). Этот метод требует значительно больше памяти; однако ряд рассматриваемой длины может анализироваться все еще очень быстро, даже если число наблюдений не является степенью 2.
| As mentioned above, the standard (and most efficient) FFT algorithm requires that the length of the input series is equal to a power of 2. If this is not the case, additional computations have to be performed. It will use the simple explicit computational formulas as long as the input series is relatively small, and the number of computations can be performed in a relatively short amount of time. For long time series, in order to still utilize the FFT algorithm, an implementation of the general approach described by Monro and Branch (1976) is used. This method requires significantly more storage space, however, series of considerable length can still be analyzed very quickly, even if the number of observations is not equal to a power of 2.
|
| Для временных рядов, длина которых не равна степени 2, мы можем дать следующие рекомендации: если размер исходного ряда не превосходит средний размер (т. е. имеется только несколько тысяч наблюдений), не стоит беспокоиться. Анализ займет несколько секунд. Для анализа средних и больших рядов (например, содержащих свыше 100, 000 наблюдений), добавьте в ряд константы (например нули) до тех пор, пока длина ряда не станет степенью 2 и затем примените косинус-сглаживание ряда в разведочной части анализа ваших данных.
| For time series of lengths not equal to a power of 2, we would like to make the following recommendations: If the input series is small to moderately sized (e. g., only a few thousand cases), then do not worry. The analysis will typically only take a few seconds anyway. In order to analyze moderately large and large series (e. g., over 100, 000 cases), pad the series to a power of 2 and then taper the series during the exploratory part of your data analysis.
|
| Дополнительная информация по методам анализа данных, добычи данных, визуализации и прогнозированию содержится на Портале StatSoft (http: //www. statsoft. ru/home/portal/default. asp) и в Углубленном Учебнике StatSoft (Учебник с формулами).
| More information on the methods of data analysis, data mining, visualization, and prediction is contained in the Portal StatSoft (http: //www. statsoft. ru/home/portal/default. asp) and in depth tutorial StatSoft (Tutorial with formulas).
|







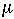 , the mean of the series; (2) if there are autoregressive parameters in the series, then the constant represents the intercept. If the series is differenced, then the constant represents the mean or intercept of the differenced series; For example, if the series is differenced once, and there are no autoregressive parameters in the model, then the constant represents the mean of the differenced series, and therefore the linear trend slope of the un-differenced series.
, the mean of the series; (2) if there are autoregressive parameters in the series, then the constant represents the intercept. If the series is differenced, then the constant represents the mean or intercept of the differenced series; For example, if the series is differenced once, and there are no autoregressive parameters in the model, then the constant represents the mean of the differenced series, and therefore the linear trend slope of the un-differenced series.


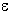 t. The constant b is relatively stable in each segment of the series, but may change slowly over time. If appropriate, then one way to isolate the true value of b, and thus the systematic or predictable part of the series, is to compute a kind of moving average, where the current and immediately preceding (" younger" ) observations are assigned greater weight than the respective older observations. Simple exponential smoothing accomplishes exactly such weighting, where exponentially smaller weights are assigned to older observations. The specific formula for simple exponential smoothing is:
t. The constant b is relatively stable in each segment of the series, but may change slowly over time. If appropriate, then one way to isolate the true value of b, and thus the systematic or predictable part of the series, is to compute a kind of moving average, where the current and immediately preceding (" younger" ) observations are assigned greater weight than the respective older observations. Simple exponential smoothing accomplishes exactly such weighting, where exponentially smaller weights are assigned to older observations. The specific formula for simple exponential smoothing is:


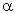 parameter can quickly be identified.
parameter can quickly be identified.
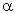 parameter (i. e., when α is close to zero), the initial value for the smoothing process can affect the quality of the forecasts for many observations. As with most other aspects of exponential smoothing it is recommended to choose the initial value that produces the best forecasts. On the other hand, in practice, when there are many leading observations prior to a crucial actual forecast, the initial value will not affect that forecast by much, since its effect will have long " faded" from the smoothed series (due to the exponentially decreasing weights, the older an observation the less it will influence the forecast).
parameter (i. e., when α is close to zero), the initial value for the smoothing process can affect the quality of the forecasts for many observations. As with most other aspects of exponential smoothing it is recommended to choose the initial value that produces the best forecasts. On the other hand, in practice, when there are many leading observations prior to a crucial actual forecast, the initial value will not affect that forecast by much, since its effect will have long " faded" from the smoothed series (due to the exponentially decreasing weights, the older an observation the less it will influence the forecast).
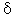 (delta). Seasonal components can be additive in nature or multiplicative. For example, during the month of December the sales for a particular toy may increase by 1 million dollars every year. Thus, we could add to our forecasts for every December the amount of 1 million dollars (over the respective annual average) to account for this seasonal fluctuation. In this case, the seasonality is additive. Alternatively, during the month of December the sales for a particular toy may increase by 40%, that is, increase by a factor of 1. 4. Thus, when the sales for the toy are generally weak, than the absolute (dollar) increase in sales during December will be relatively weak (but the percentage will be constant); if the sales of the toy are strong, than the absolute (dollar) increase in sales will be proportionately greater. Again, in this case the sales increase by a certain factor, and the seasonal component is thus multiplicative in nature (i. e., the multiplicative seasonal component in this case would be 1. 4). In plots of the series, the distinguishing characteristic between these two types of seasonal components is that in the additive case, the series shows steady seasonal fluctuations, regardless of the overall level of the series; in the multiplicative case, the size of the seasonal fluctuations vary, depending on the overall level of the series.
(delta). Seasonal components can be additive in nature or multiplicative. For example, during the month of December the sales for a particular toy may increase by 1 million dollars every year. Thus, we could add to our forecasts for every December the amount of 1 million dollars (over the respective annual average) to account for this seasonal fluctuation. In this case, the seasonality is additive. Alternatively, during the month of December the sales for a particular toy may increase by 40%, that is, increase by a factor of 1. 4. Thus, when the sales for the toy are generally weak, than the absolute (dollar) increase in sales during December will be relatively weak (but the percentage will be constant); if the sales of the toy are strong, than the absolute (dollar) increase in sales will be proportionately greater. Again, in this case the sales increase by a certain factor, and the seasonal component is thus multiplicative in nature (i. e., the multiplicative seasonal component in this case would be 1. 4). In plots of the series, the distinguishing characteristic between these two types of seasonal components is that in the additive case, the series shows steady seasonal fluctuations, regardless of the overall level of the series; in the multiplicative case, the size of the seasonal fluctuations vary, depending on the overall level of the series.






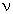 = 0. 0625 and
= 0. 0625 and 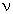 =. 1875 suggest two strong synchronized periodicities in both series at those frequencies. In fact, the two series were created as:
=. 1875 suggest two strong synchronized periodicities in both series at those frequencies. In fact, the two series were created as:


 0)
0)