
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задача 1.. Задача 2.. Задача 3.. Задача 4.. Задача 5.. Задача7.. Задача 8.. Задача 9.. Задача 10.. Задача 14.
Задача 1.
1. 9.
Дана функция 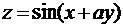 .
.
Показать, что 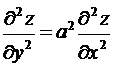 .
.
Задача 2.
Найти наименьшее и наибольшее значения функции z=f(x, y) в ограниченной замкнутой области D, заданной системой неравенств. Сделать чертеж.
2. 9.
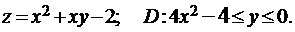
Задача 3.
Дана функция z=z(x, y), точка А(х0, у0) и вектор 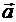 . Найти: 1)
. Найти: 1) 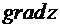 в точке A; 2) производную в точке A по направлению вектора
в точке A; 2) производную в точке A по направлению вектора 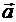 .
.
3. 9.
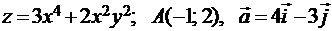 .
.
Задача 4.
Найти неопределенные интегралы. В двух примерах (пункты а) и б)) проверить результаты дифференцированием.
4. 9.
а) 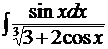 ; б)
; б) 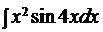 ;
;
в) 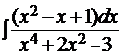 ; г)
; г) 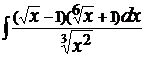 .
.
Задача 5.
Вычислить несобственный интеграл или доказать его расходимость.
5. 9.
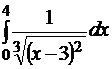 .
.
Задача 6.
Найти общее решение дифференциального уравнения.
6. 9.
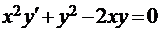 .
.
Задача7.
Найти частное решение дифференциального уравнения 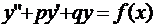 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям 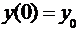 ,
, 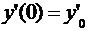 .
.
7. 9.
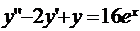 ;
;  ,
, 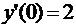 .
.
Задача 8.
Вычислить двойные интегралы по области D.
8. 9.
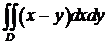 , где D – область, ограниченная линиями
, где D – область, ограниченная линиями 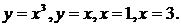
Задача 9.
Перейдя к полярным координатам (если требуется), вычислить площадь фигуры, ограниченной областью D.
9. 9.
Область D ограниченна линиями: 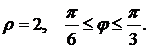
Задача 10.
Вычислить криволинейные интегралы 2-го рода
10. 9.
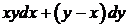 вдоль линии
вдоль линии 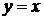 от точки О (0; 0) до точки А(1; 1).
от точки О (0; 0) до точки А(1; 1).
Задача 11.
Исследовать сходимость числового ряда.
12. 9.
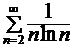 .
.
Задача 13.
Найти интервал сходимости степенного ряда.
13. 9.
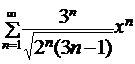 .
.
Задача 14.
Вычислить определенный интеграл 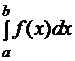 с точностью до 0, 001, разложив подынтегральную функцию в ряд, и, затем, проинтегрировав ее почленно.
с точностью до 0, 001, разложив подынтегральную функцию в ряд, и, затем, проинтегрировав ее почленно.
14. 9.
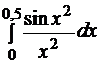 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|