Листик № 1 Вводный

Графом называется непустое множество точек, некоторые из которых соединены отрезками.

задача 1. Доска имеет форму креста, который получается, если из квадратной доски 4´ 4 выкинуть угловые клетки. Можно ли обойти ее ходом шахматного коня и вернуться на исходное поле, побывав на всех полях ровно по одному разу?

задача 2. В 20-ти этажном доме испорчен лифт - он может либо подниматься на 8 этажей вверх, либо спускаться на 13 этажей вниз. Можно ли с помощью лифта попасть с 20 этажа на 1-й? (когда сверху меньше 8-ми этажей, то лифт вверх не поедет. Аналогично вниз. )

задача 3. На консультации было 20 школьников и разбиралось 20 задач. Оказалось, что каждый школьник решил две задачи и каждую задачу решили два школьника. Докажите, что можно так организовать разбор задач, чтобы каждый рассказал одну задачу и все задачи были рассказаны.

задача 4. В государстве 2006 городов, и из каждого из них выходит семь дорог. Сколько дорог в государстве?

Степенью вершины называется число ребер графа, которым принадлежит эта вершина.

задача 5. Докажите, что в графе сумма степеней всех его вершин - число четное, равное удвоенному числу ребер графа.

задача 6. Может ли в государстве, в котором из каждого города выходит 3 дороги, быть ровно 100 дорог?

задача 7. Существует ли граф с шестью вершинами, степени которых равны 2, 3, 3, 4, 4, 4?

задача 8. В городе отличников от каждой площади отходит 5 улиц. Докажите, что число площадей четно, а число улиц делится на 5.

задача 9. Девять шахматистов проводят турнир в один круг (каждый из участников должен сыграть с каждым из остальных по одному разу). Докажите, что в любой момент турнира найдутся двое, закончившие одинаковое число партий.

задача 10. Докажите, что если в графе с 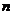вершинами ( 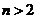) ровно две вершины имеют одинаковую степень, то в этом графе всегда найдется либо ровно одна вершина степени 0, либо ровно одна вершина степени .

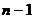задача 11. В городе Маленьком 15 телефонов. Можно ли их соединить проводами так, чтобы каждый был соединен ровно с 5 другими?

Вершина называется четной (нечетной), если ее степень четна (нечетна).

задача 12. Докажите, что число нечетных вершин любого графа четно.

задача 13. В классе 30 человек. Может ли быть так, что 9 из них имеют по 3 друга (в этом классе), 11 - по 4 друга, а 10 - по 5 друзей?

задача 14. Докажите, что число людей, когда-либо живших на Земле и сделавших нечетное число рукопожатий, четно.

задача 15. Можно ли нарисовать на плоскости 9 отрезков так, чтобы каждый пересекался ровно с тремя другими?

задача 16. Участники слета, познакомившись, обменялись конвертами с адресами. Докажите, что всего было передано четное число конвертов. Докажите, что число участников, обменявшихся конвертами нечетное число раз, четное.

задача 17. В футбольном турнире участвуют 29 команд. Докажите, что в любой момент найдется команда, сыгравшая четное число матчей.

Вершина называются изолированной, если она не принадлежит ни одному ребру.

Граф называется полным, если каждые две различные вершины его соединены единственным ребром.

задача 18. Существует ли полный граф с 7 ребрами?

Дополнением графа 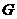называется граф 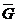с теми же вершинами, что и граф 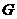, и с теми и только теми ребрами, которые необходимо добавить к графу 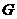, чтобы получился полный граф.

задача 19. В некотором графе существуют ровно две вершины, из которых выходит одинаковое число ребер. Сколько таких вершин (вершин, из которых выходит одинаковое число ребер) может быть в дополнении этого графа?

задача 20. В графе с пятью вершинами ровно две вершины имеют одинаковую степень. Могут ли они обе быть изолированными или обе иметь степень 4?