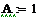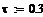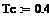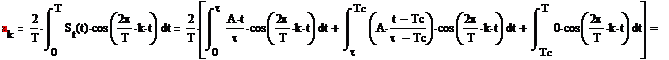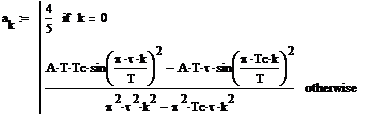- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Синусный коэффициент считается аналогично, с одним изменением эти несколько интегралов умножатся на соответствующий синус
Объясню на примере своей задачи
Вот что у меня дано
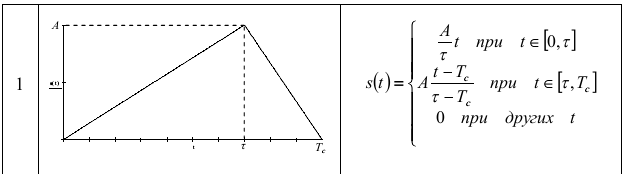
|
|
| < -- а м п л и т у д а и м п у л ь с н о г о с и г н а л а |
|
|
| < -- п о с т о я н н а я в р е м е н и и м п у л ь с н о г о с и г н а л а |
|
|
| < -- д л и т е л ь н о с т ь и м п у л ь с н о г о с и г н а л а |
| < -- п е р и о д |
|
|
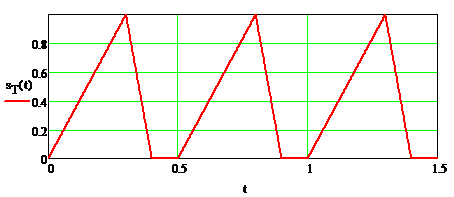
А вот мой график периодического сигнала ( ну наверно все её строили)
|
|
Косинусный коэффициент Фурье: 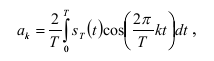
Под ST(t) понимается все уравнения линий, которые у вас рисуются от промежутке от 0 до Т, даже та часть (она у всех есть), где идет просто нулевая линия, после которой все снова повторяется.
У меня линия в периоде описывается 3-мя функциями, смотри на рисунок внизу
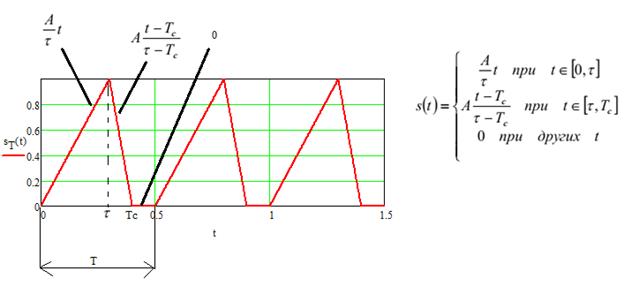
Ваше выражение косинусого коэффициента превратится в выражение 2/T умноженная на сумму нескольких интегралов, вот у меня St(t) разделился на:
интеграл от 0 до τ функция 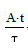 умноженная косинус
умноженная косинус 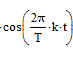
плюс
интеграл от τ до T функция на этом участке и умноженная косинус
и нуль( почему там нуль должно быть ясно) на косинус
|
|
Принцип на какие интегралы я поделил надеюсь ясен( все же, блин, изучали как площадь сложной формы интегралами высчитываются)
В этом сложном выражении надо раскрыть интегралы, упростить и получите в итоге то что записываете во 2 строке, где otherwise. При k=0 соответственно в полученное сложное выражение k заменить на 0, дальше также все раскрыть, упростить.
|
|
Маткад умеет раскрывать и упрощать такие сложные выражения
Выделяете её Символьные операции –> упростить
Синусный коэффициент считается аналогично, с одним изменением эти несколько интегралов умножатся на соответствующий синус
В выкладке придется пошагово расписывать как вы раскрывали интегралы, упрощали и получили итоговое выражение
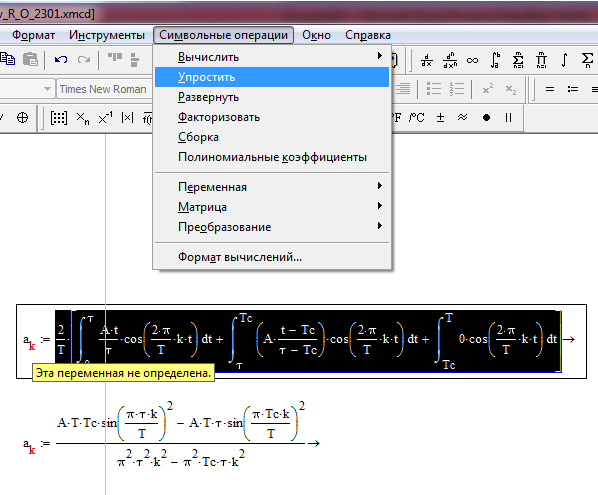
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|