3. ВАРИАНТЫ ДЛЯ ВЫПОЛНЕНИЯ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ

ЛАБОРАТОРНАЯ РАБОТА №7

ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ. ИНТЕРПОЛЯЦИОННЫЕ ФОРМУЛЫ НЬЮТОНА.

Цель работы: используя интерполяционную формулу, найти значение функции в точке, не являющейся табличной, и оценить погрешность метода решения; подобрать аналитическую формулу, представляющую с некоторой точностью данные табличные значения функции.

2 ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ

1. Составить таблицу значений функции, приведенной в табл. 1, разбив заданный интервал на 10 отрезков с h=const.

2. Составить таблицу конечных разностей.

3. По первой и второй интерполяционным формулам Ньютона определить значение функции в точках

х = х₀ ± 0. 25h;

х = х₀ ± 0. 5h;

х = x_l₀ ± 0. 25h;

х = x_l₀ ±0. 5h;

4. Построить эмпирическую формулу для заданной функции.

5. Выполнить программную реализацию построения таблицы конечных разностей и эмпирической формулы, а так же расчет значений функций в точках из п. 3.

6. Результаты вычислений свести в таблицу вида:

x	y(x)	q	P_n(x)	Погрешность

3. ВАРИАНТЫ ДЛЯ ВЫПОЛНЕНИЯ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ

Таблица 1

№ п/п	Функция	Интервал
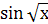
		0; 1
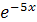
		0; 1
	cos(x²)	0; 0. 5
	tg(x³)	0; 0. 5
	arctg( )	1; 11
	ln(sin(x))	π /4; 3π /4
	cos(e^x)	1; 2
	tg	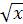0; 2
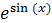
		0; 1
	sin(ln(x))	0. 1; 1. 1
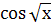
		0; 2
	sin x²	0; 1
	ln	1; 2
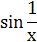
		π /4; 5π /4
	arcsin	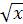0; 0. 5