Performance of work

Nonprofit " Almaty University of Power Engineering & Telecommunications"

The faculty of electrical power engineering

Department of " Electronics and Robotics"

Laboratory work №4

On discipline: Theory of automatic control

On the topic: System stability by criterion Nyquist

Specialty: Instrument making – 5B071600

Completed: Kassymov M. S.

Prepared by assistant lecturer: Ayazbai Abu-Alim

________________ «___»________________2018

(evalution) (signature)

Almaty 2018

Laboratory work №4. System stability by criterion Nyquist

Aim of work: definition of frequency response and phase response of an open and closed systems, and the determination of sustainability by the Nyquist criterion and the form of LAFC open system.

Theory

Frequency Based Nyquist Criterion characteristics, allows to judge about the stability of a closed ACS by its amplitude-phase response in the open state.
Curve (Figure 4. 1, b) representing frequency response stable system, intersects with the x-axis to the right of the point (-1; j0) and called the amplitude-phase characteristic of the first kind. Curve (Fig. 1, a), intersecting with the x-axis both to the right and to the left of the point (-1; j0), called the amplitude-phase characteristic of the second kind. In this case the system in a closed state will be stable under the condition that the difference between the number of positive (top down) and negative (bottom up) transitions of the amplitude-phase characteristics through the x-axis to the left of points (-1; j0) is equal to zero.

In general, if the degree of the numerator polynomial is less than denominator polynomial of the FS of an open-loop system and they do not have common roots with a nonnegative real part, the second Nyquist criterion is formulated as follows: ACS, unstable in open state is stable in the closed state if the difference between the numbers of positive and negative transitions of AFC through the x-axis to the left of the point (-1; j0) is r / 2. Formulated first criterion Nyquist stability should be considered as a special case of general problems with r = 0 (r is the number of right roots of the characteristic equation open system).

When analyzing the stability of the system in amplitude-phase characteristics it is advisable to introduce the concept of sustainability module and phase. If through the point (-1; j0) (Fig. 1, b) draw a circle unit radius, we obtain its intersection point with the amplitude-phase characteristic. The stability margin modulo is characterized by the segment h, and margin of stability in phase - angle φ з. The method is based on the possibility of judging stability closed system by the mutual arrangement of logarithmic amplitude and phase characteristics of the system in the open state. According to the Nyquist criterion, if the system is stable, the point (-1; j0) lies to the left of AFC of the first kind.
In order for a stable open system to be it is stable also in a closed state, it is necessary and sufficient that the difference between the number of positive and negative transitions phase characteristic φ (ω ) through a straight line (-π ) at the same values of ω, for which LAFC is non-negative, equals zero.

Performance of work

1) Collect the given closed system and get the acceleration curve at K = 0. 9 and K = 6. 2.

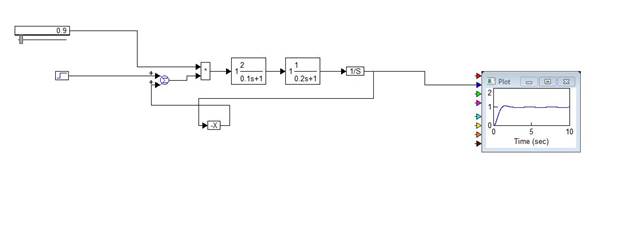
Figure 4. 4 - Acceleration curve of a stable closed system at K = 0. 9

The block of the generator of constant signals slider is in the menu block Blocks Signal producer- slider. In the circuit, it serves as a regulator.

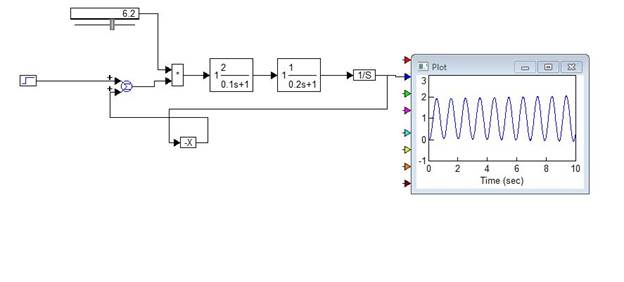
Figure 4. 5 - Acceleration curve of an unstable closed system with K = 6. 2

2) Remove the frequency response and phase response of open systems at K = 0. 5. This requires a block to measure the amplitude and phase ratio mag_has, which is in the Diagrams-Toolbox-Tools-Magnitude menu box Phase. Then you need to make a copy of it and put it in the main circuit window: select selection - Edit-Copy - close the Magnitude Phase window. In the main window programs to insert block mag_has: Edit-Paste. By installing in the Sin block amplitude 1, Td = 0. 1s and changing the frequency in it, write in the form of a table measured values of A (ω ) and φ (ω ). It is important to catch the frequency at which the ratio of the amplitudes will be equal to 1 - the upper indicator reading

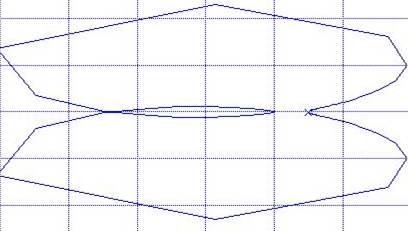
Figure 4. 6 - the frequency response and phase response of an open-loop system at f = 1. 6 rad / s

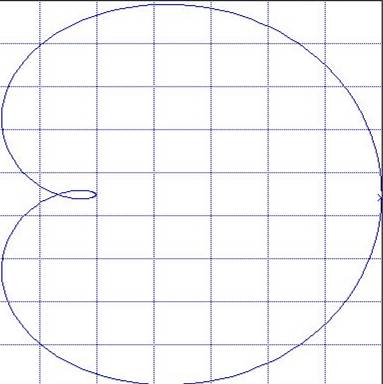
Figure 4. 7 - frequency response and phase response of an open-loop system at f = 3 rad / s
3) Remove the frequency response and phase response of open-loop systems at K = 6. 2, i. e. repeat paragraph 2.

Conclusion

In this laboratory work, I learned how to collect the given closed system and get the acceleration curve at K = 0. 9 and K = 6. 2.

I removed the frequency response and phase response of open systems at K = 0. 9.