
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
КОЭФФИЦИЕНТЫ ГРАФИКИ
1. Найдите значение выражения: 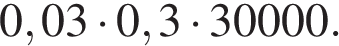
2. Площадь территории России составляет 1, 7 · 107 км2, а Норвегии — 3, 2⋅ 105 км2. Во сколько раз площадь территории России больше площади территории Норвегии?
В ответе укажите номер правильного варианта.
1) примерно в 1, 9 раза, 2) примерно в 5, 3 раза, 3) примерно в 53 раза, 4) примерно в 530 раз
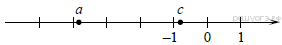
3. На координатной прямой отмечены числа 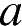 и
и 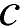 :
:
Какое из следующих утверждений неверно?
1) 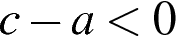 : 2)
: 2) 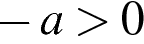 ; 3)
; 3) 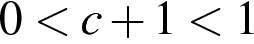 ; 4)
; 4) 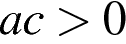
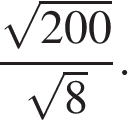
4. Найдите значение выражения
 В ответе укажите номер правильного варианта.
В ответе укажите номер правильного варианта.
1) 5; 2)  ; 3)
; 3)  ; 4) 40
; 4) 40
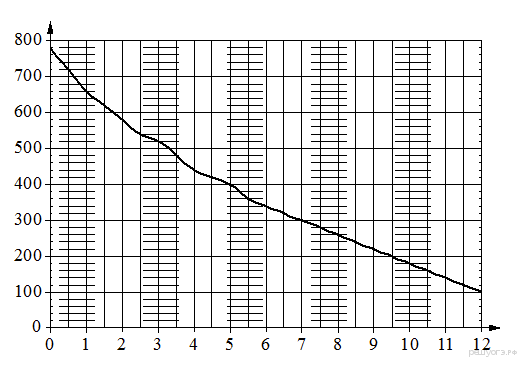
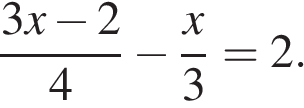 5. На графике изображена зависимость атмосферного давления от высоты над уровнем моря. На горизонтальной оси отмечена высота над уровнем моря в километрах, на вертикальной — давление в миллиметрах ртутного столба. Определите по графику, чему равно атмосферное давление на высоте 5 км над уровнем моря. Ответ дайте в миллиметрах ртутного столба.
5. На графике изображена зависимость атмосферного давления от высоты над уровнем моря. На горизонтальной оси отмечена высота над уровнем моря в километрах, на вертикальной — давление в миллиметрах ртутного столба. Определите по графику, чему равно атмосферное давление на высоте 5 км над уровнем моря. Ответ дайте в миллиметрах ртутного столба.
6. Решите уравнение:
7. Дневная норма потребления витамина С составляет 60 мг. Один мандарин в среднем содержит 35 мг витамина С. Сколько процентов дневной нормы витамина С получил человек, съевший один мандарин? Ответ округлите до целых.
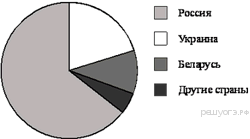
8. На диаграмме представлено распределение количества пользователей некоторой социальной сети по странам мира. Всего в этой социальной сети 9 млн пользователей.
Какое из следующих утверждений неверно?
1) Пользователей из России больше, чем пользователей из Беларуси.
2) Пользователей из Украины меньше трети общего числа пользователей.
3) Пользователей из Беларуси больше, чем пользователей из Дании.
4) Пользователей из России меньше 4 миллионов.
9. Стрелок три раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0, 7. Найдите вероятность того, что стрелок первые два раза попал в мишени, а последний раз промахнулся.
10. На рисунках изображены графики функций вида 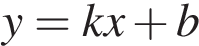 . Установите соответствие между знаками коэффициентов
. Установите соответствие между знаками коэффициентов  и
и 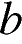 и графиками функций.
и графиками функций.
КОЭФФИЦИЕНТЫ ГРАФИКИ
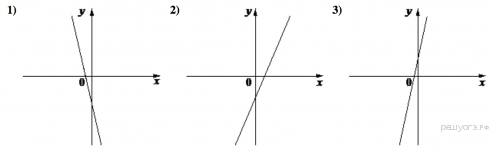
А) 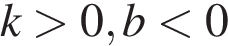
Б) 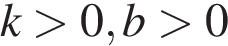
В) 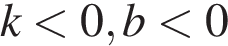
11. Выписаны первые несколько членов геометрической прогрессии: − 175; − 140; − 112; ... Найдите её пятый член.
12. Найдите значение выражения 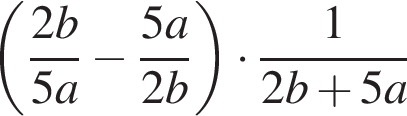 при
при 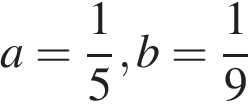
13. Закон всемирного тяготения можно записать в виде 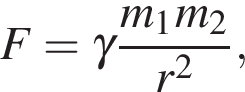 где
где 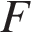 — сила притяжения между телами (в ньютонах),
— сила притяжения между телами (в ньютонах),  и
и  — массы тел (в килограммах),
— массы тел (в килограммах),  — расстояние между центрами масс (в метрах), а
— расстояние между центрами масс (в метрах), а  — гравитационная постоянная, равная 6. 67 · 10− 11 H·м2/кг2. Пользуясь формулой, найдите массу тела
— гравитационная постоянная, равная 6. 67 · 10− 11 H·м2/кг2. Пользуясь формулой, найдите массу тела  (в килограммах), если
(в килограммах), если  Н,
Н, 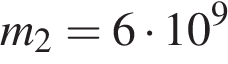 кг, а
кг, а  м.
м.
14. Решите неравенство 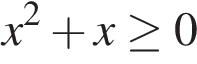 .
.
В ответе укажите номер правильного варианта.
1)  2)
2) 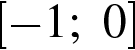 3)
3) 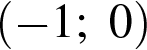 4)
4) 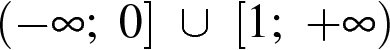
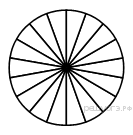
15. Колесо имеет 18 спиц. Углы между соседними спицами равны. Найдите угол, который образуют две соседние спицы. Ответ дайте в градусах.
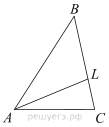
16. В треугольнике ABC проведена биссектриса AL, угол ALC равен 62°, угол ABC равен 47°. Найдите угол ACB. Ответ дайте в градусах.
17. В треугольнике ABC угол C равен 90°, AC = 10, tgA = 0, 5. Найдите BC.
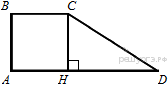 18. Тангенс острого угла прямоугольной трапеции равен
18. Тангенс острого угла прямоугольной трапеции равен  . Найдите её большее основание, если меньшее основание равно высоте и равно 55.
. Найдите её большее основание, если меньшее основание равно высоте и равно 55.
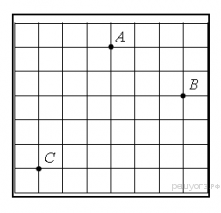
19. На клетчатой бумаге с размером клетки 1 см × 1 см отмечены точки A, B и C. Найдите расстояние от точки A до середины отрезка BC. Ответ выразите в сантиметрах.
20. Какое из следующих утверждений верно?
1. Площадь прямоугольного треугольника равна произведению длин его катетов.
2. Существует прямоугольник, диагонали которого взаимно перпендикулярны.
3. Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны.
В ответ запишите номер выбранного утверждения.
21. Решите уравнение 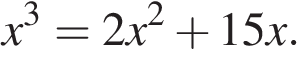
22. Имеется два сплава с разным содержанием меди: в первом содержится 70%, а во втором — 40% меди. В каком отношении надо взять первый и второй сплавы, чтобы получить из них новый сплав, содержащий 50% меди?
23. Найдите все значения k, при каждом из которых прямая y = kx имеет с графиком функции y = x2+ 4 ровно одну общую точку. Постройте этот график и все такие прямые.
24. Стороны AC, AB, BC треугольника ABC равны 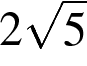 ,
, 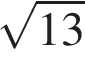 и 1 соответственно. Точка K расположена вне треугольника ABC, причём отрезок KC пересекает сторону AB в точке, отличной от B. Известно, что треугольник с вершинами K, A и C подобен исходному. Найдите косинус угла AKC, если ∠ KAC> 90°.
и 1 соответственно. Точка K расположена вне треугольника ABC, причём отрезок KC пересекает сторону AB в точке, отличной от B. Известно, что треугольник с вершинами K, A и C подобен исходному. Найдите косинус угла AKC, если ∠ KAC> 90°.
25. Дан правильный шестиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится равносторонний треугольник.
26. Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади четырёхугольника KPCM к площади треугольника AMK.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|