ТЕМА 1.2 ОСНОВНЫЕ ВИДЫ СИГНАЛОВ. МОДУЛИРОВАННЫЕ СИГНАЛЫ

ТЕМА 1. 2 ОСНОВНЫЕ ВИДЫ СИГНАЛОВ. МОДУЛИРОВАННЫЕ СИГНАЛЫ

ВОПРОС 3 АМПЛИТУДНО-МОДУЛИРОВАННЫЕ СИГНАЛЫ. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ АМ СИГНАЛА, ЕГО СПЕКТР. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ПРОЦЕССА МОДУЛЯЦИИ

При амплитудной модуляции в соответствии с законом передаваемого сообщения меняется амплитуда модулируемого сигнала. Поэтому при тестовом тональном модулирующем сигнале имеем для высокочастотного модулируемого сигнала

u_ам(t) = U₀ * (1+m* cosΩ t) * cos ω ₀t

(1)

где т = U_МОД/U₀ ≤ 1 – коэффициент амплитудной модуляции;

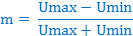
ω ₀– частота несущих колебаний.

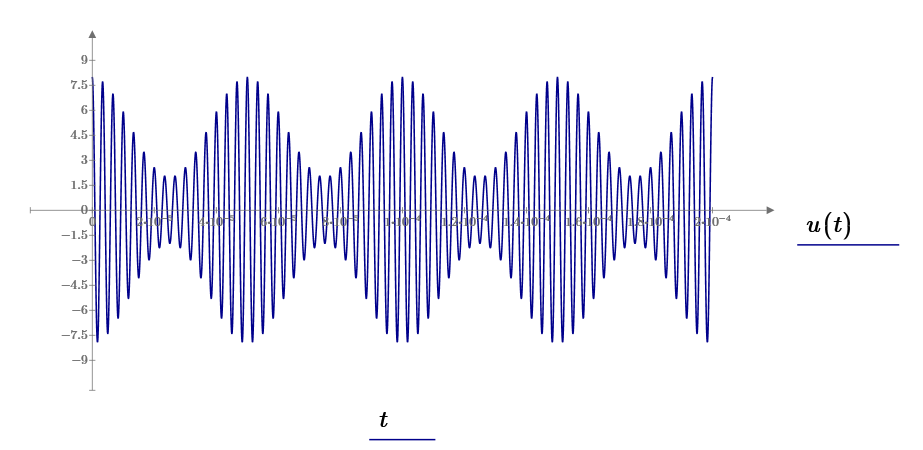
График функции (1), который можно наблюдать на экране осциллографа, приведен на рисунке 1.

m = 0. 8

Рисунок 1 – Амплитудно-модулированный сигнал

Амплитуда ВЧ колебаний и мощность при тональной АМ модуляции меняются по закону:

(2)

Согласно данным выражениям мгновенные мощности ВЧ сигнала в трех режимах — молчания, максимальном (пиковом) и минимальном — связаны соотношениями:

(3)

Кроме мгновенных, важна и средняя мощность ВЧ колебаний за период модулирующего сигнала Т.

(4)

Из трех последних формул при т = 1 получим:

Отметим, что пиковая мощность генератора при амплитудной модуляции должна в четыре раза превосходить мощность в режиме несущей (молчания).

Спектр АМ колебания можно получить, представив (1) в соответствии с правилами тригонометрии в виде

(5)

из которого следует, что спектр колебания при амплитудной модуляции тональным сигналом состоит из трех составляющих с частотами:

ω ₀ (совпадает с частотой несущей),

ω ₀– Ω (нижняя боковая),

ω ₀+ Ω (верхняя боковая), мощности между которыми распределены в пропорции:

1: (0, 5m²): (0, 5m²) (рисунок 2, а).

Спектр АМ колебания при модуляции сигналом, занимающим спектр от Ω _миндо Ω _макс, представлен на рисунке 2, б.

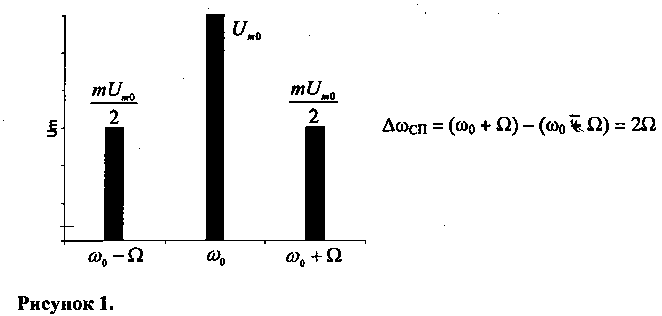
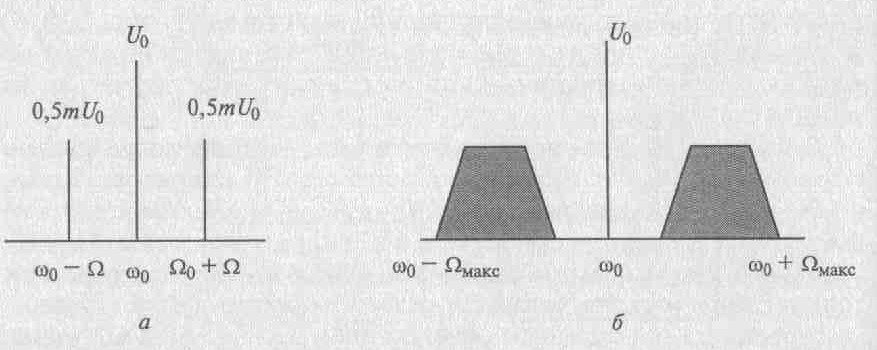
Рисунок 2 – Спектр АМ сигнала

Ширина спектра АМ колебания, построенного на рисунке 2, а: ∆ fсп = 2F.

Амплитуды боковых частот зависят от коэффициента модуляции m. Частоты боковых составляющих отличаются от несущей на управляющую.

ПРИМЕРЫ АМ СИГНАЛОВ ПРИ РАЗЛИЧНЫХ ЗНАЧЕНИЯХ КОЭФФИЦИЕНТА МОДУЛЯЦИИ

m = 0. 6

m = 0. 2

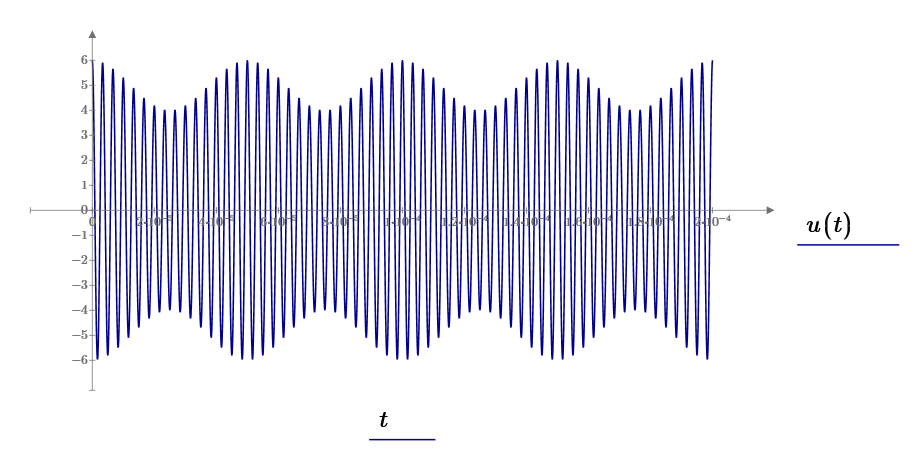
m = 0. 9

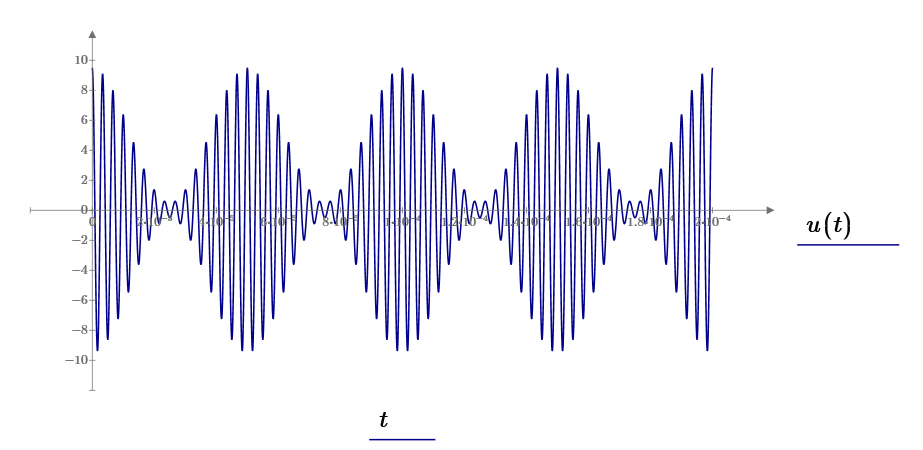
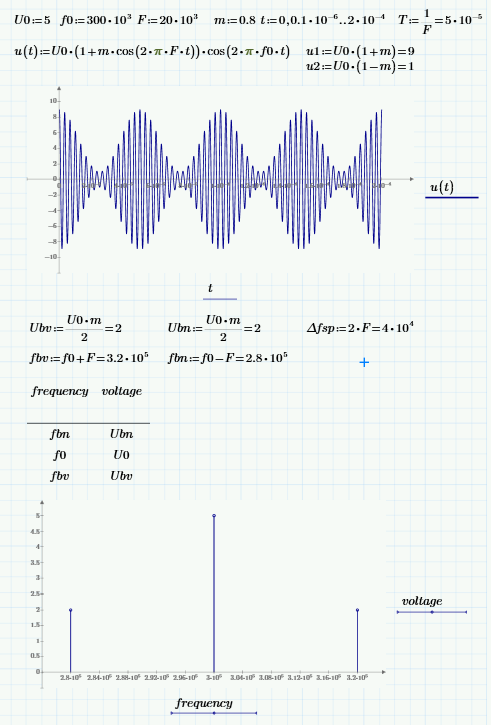
Задача 1 Написать математическое выражение амплитудно-модулированного сигнала. Построить АМ-сигнал и его спектр. Определить ширину спектра АМ-сигнала.

Значения коэффициента модуляции m, амплитуды U и частоты f несущего колебания, частоты моделирующего колебания F приведены в таблице.

Амплитуда высокочастотного колебания U, В	Частота высокочастотного колебания f*100, кГц	Частота модулирующего колебания F, кГц	коэффициента модуляции m
			0. 8